Exploiting Exogenous Structure for Sample-Efficient Reinforcement Learning
Paper and Code
Sep 22, 2024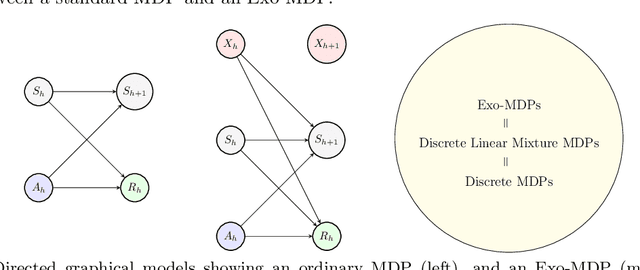
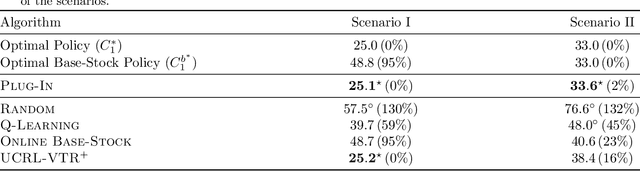
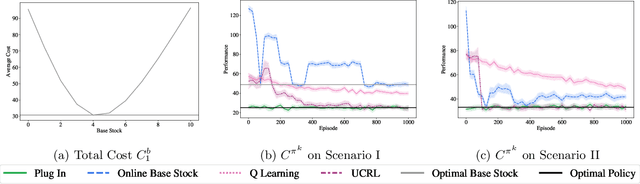
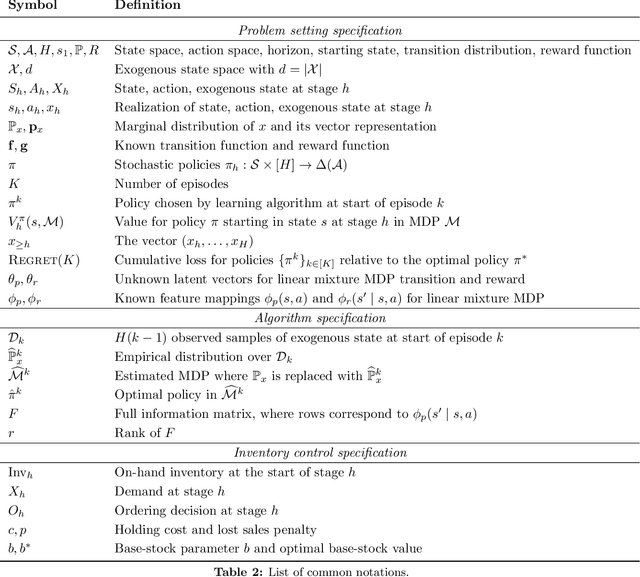
We study a class of structured Markov Decision Processes (MDPs) known as Exo-MDPs, characterized by a partition of the state space into two components. The exogenous states evolve stochastically in a manner not affected by the agent's actions, whereas the endogenous states are affected by the actions, and evolve in a deterministic and known way conditional on the exogenous states. Exo-MDPs are a natural model for various applications including inventory control, finance, power systems, ride sharing, among others. Despite seeming restrictive, this work establishes that any discrete MDP can be represented as an Exo-MDP. Further, Exo-MDPs induce a natural representation of the transition and reward dynamics as linear functions of the exogenous state distribution. This linear representation leads to near-optimal algorithms with regret guarantees scaling only with the (effective) size of the exogenous state space $d$, independent of the sizes of the endogenous state and action spaces. Specifically, when the exogenous state is fully observed, a simple plug-in approach achieves a regret upper bound of $O(H^{3/2}\sqrt{dK})$, where $H$ denotes the horizon and $K$ denotes the total number of episodes. When the exogenous state is unobserved, the linear representation leads to a regret upper bound of $O(H^{3/2}d\sqrt{K})$. We also establish a nearly matching regret lower bound of $\Omega(Hd\sqrt{K})$ for the no observation regime. We complement our theoretical findings with an experimental study on inventory control problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge