Adaptive Discretization for Model-Based Reinforcement Learning
Paper and Code
Jul 01, 2020
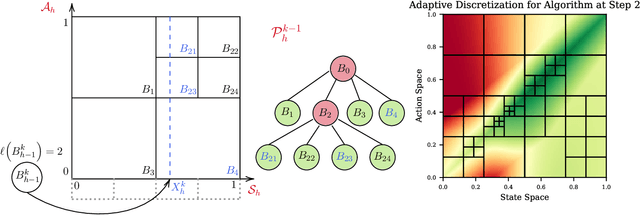
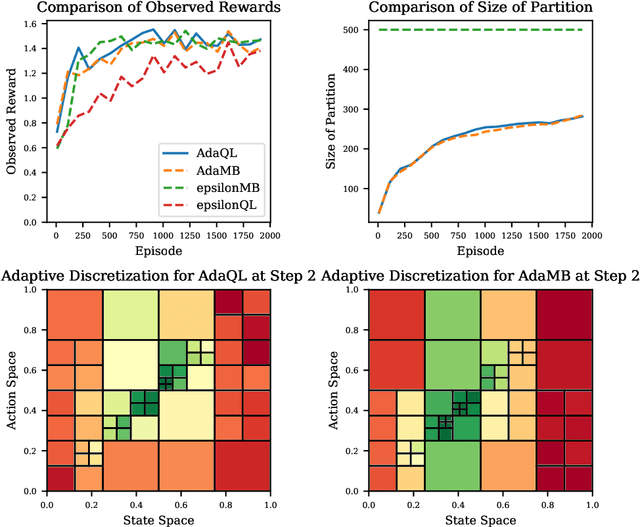

We introduce the technique of adaptive discretization to design efficient model-based episodic reinforcement learning algorithms in large (potentially continuous) state-action spaces. Our algorithm is based on optimistic one-step value iteration extended to maintain an adaptive discretization of the space. From a theoretical perspective, we provide worst-case regret bounds for our algorithm, which are competitive compared to the state-of-the-art model-based algorithms; moreover, our bounds are obtained via a modular proof technique, which can potentially extend to incorporate additional structure on the problem. From an implementation standpoint, our algorithm has much lower storage and computational requirements, due to maintaining a more efficient partition of the state and action spaces. We illustrate this via experiments on several canonical control problems, which shows that our algorithm empirically performs significantly better than fixed discretization in terms of both faster convergence and lower memory usage. Interestingly, we observe empirically that while fixed-discretization model-based algorithms vastly outperform their model-free counterparts, the two achieve comparable performance with adaptive discretization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge