IRL for Restless Multi-Armed Bandits with Applications in Maternal and Child Health

Public health practitioners often have the goal of monitoring patients and maximizing patients' time spent in "favorable" or healthy states while being constrained to using limited resources. Restless multi-armed bandits (RMAB) are an effective model to solve this problem as they are helpful to allocate limited resources among many agents under resource constraints, where patients behave differently depending on whether they are intervened on or not. However, RMABs assume the reward function is known. This is unrealistic in many public health settings because patients face unique challenges and it is impossible for a human to know who is most deserving of any intervention at such a large scale. To address this shortcoming, this paper is the first to present the use of inverse reinforcement learning (IRL) to learn desired rewards for RMABs, and we demonstrate improved outcomes in a maternal and child health telehealth program. First we allow public health experts to specify their goals at an aggregate or population level and propose an algorithm to design expert trajectories at scale based on those goals. Second, our algorithm WHIRL uses gradient updates to optimize the objective, allowing for efficient and accurate learning of RMAB rewards. Third, we compare with existing baselines and outperform those in terms of run-time and accuracy. Finally, we evaluate and show the usefulness of WHIRL on thousands on beneficiaries from a real-world maternal and child health setting in India. We publicly release our code here: https://github.com/Gjain234/WHIRL.

Adaptive Discretization for Model-Based Reinforcement Learning

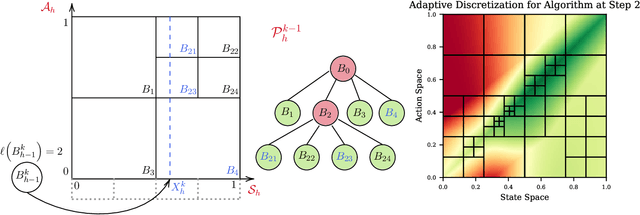
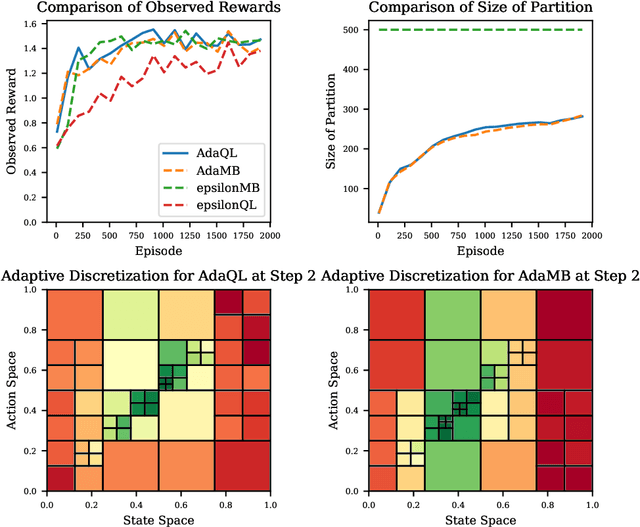
We introduce the technique of adaptive discretization to design efficient model-based episodic reinforcement learning algorithms in large (potentially continuous) state-action spaces. Our algorithm is based on optimistic one-step value iteration extended to maintain an adaptive discretization of the space. From a theoretical perspective, we provide worst-case regret bounds for our algorithm, which are competitive compared to the state-of-the-art model-based algorithms; moreover, our bounds are obtained via a modular proof technique, which can potentially extend to incorporate additional structure on the problem. From an implementation standpoint, our algorithm has much lower storage and computational requirements, due to maintaining a more efficient partition of the state and action spaces. We illustrate this via experiments on several canonical control problems, which shows that our algorithm empirically performs significantly better than fixed discretization in terms of both faster convergence and lower memory usage. Interestingly, we observe empirically that while fixed-discretization model-based algorithms vastly outperform their model-free counterparts, the two achieve comparable performance with adaptive discretization.