FRESHR-GSI: A Generalized Safety Model and Evaluation Framework for Mobile Robots in Multi-Human Environments

Human safety is critical in applications involving close human-robot interactions (HRI) and is a key aspect of physical compatibility between humans and robots. While measures of human safety in HRI exist, these mainly target industrial settings involving robotic manipulators. Less attention has been paid to settings where mobile robots and humans share the space. This paper introduces a new robot-centered directional framework of human safety. It is particularly useful for evaluating mobile robots as they operate in environments populated by multiple humans. The framework integrates several key metrics, such as each human's relative distance, speed, and orientation. The core novelty lies in the framework's flexibility to accommodate different application requirements while allowing for both the robot-centered and external observer points of view. We instantiate the framework by using RGB-D based vision integrated with a deep learning-based human detection pipeline to yield a generalized safety index (GSI) that instantaneously assesses human safety. We evaluate GSI's capability of producing appropriate, robust, and fine-grained safety measures in real-world experimental scenarios and compare its performance with extant safety models.

Inversely Learning Transferable Rewards via Abstracted States

Inverse reinforcement learning (IRL) has progressed significantly toward accurately learning the underlying rewards in both discrete and continuous domains from behavior data. The next advance is to learn {\em intrinsic} preferences in ways that produce useful behavior in settings or tasks which are different but aligned with the observed ones. In the context of robotic applications, this helps integrate robots into processing lines involving new tasks (with shared intrinsic preferences) without programming from scratch. We introduce a method to inversely learn an abstract reward function from behavior trajectories in two or more differing instances of a domain. The abstract reward function is then used to learn task behavior in another separate instance of the domain. This step offers evidence of its transferability and validates its correctness. We evaluate the method on trajectories in tasks from multiple domains in OpenAI's Gym testbed and AssistiveGym and show that the learned abstract reward functions can successfully learn task behaviors in instances of the respective domains, which have not been seen previously.

Visual IRL for Human-Like Robotic Manipulation

We present a novel method for collaborative robots (cobots) to learn manipulation tasks and perform them in a human-like manner. Our method falls under the learn-from-observation (LfO) paradigm, where robots learn to perform tasks by observing human actions, which facilitates quicker integration into industrial settings compared to programming from scratch. We introduce Visual IRL that uses the RGB-D keypoints in each frame of the observed human task performance directly as state features, which are input to inverse reinforcement learning (IRL). The inversely learned reward function, which maps keypoints to reward values, is transferred from the human to the cobot using a novel neuro-symbolic dynamics model, which maps human kinematics to the cobot arm. This model allows similar end-effector positioning while minimizing joint adjustments, aiming to preserve the natural dynamics of human motion in robotic manipulation. In contrast with previous techniques that focus on end-effector placement only, our method maps multiple joint angles of the human arm to the corresponding cobot joints. Moreover, it uses an inverse kinematics model to then minimally adjust the joint angles, for accurate end-effector positioning. We evaluate the performance of this approach on two different realistic manipulation tasks. The first task is produce processing, which involves picking, inspecting, and placing onions based on whether they are blemished. The second task is liquid pouring, where the robot picks up bottles, pours the contents into designated containers, and disposes of the empty bottles. Our results demonstrate advances in human-like robotic manipulation, leading to more human-robot compatibility in manufacturing applications.

IRL for Restless Multi-Armed Bandits with Applications in Maternal and Child Health

Public health practitioners often have the goal of monitoring patients and maximizing patients' time spent in "favorable" or healthy states while being constrained to using limited resources. Restless multi-armed bandits (RMAB) are an effective model to solve this problem as they are helpful to allocate limited resources among many agents under resource constraints, where patients behave differently depending on whether they are intervened on or not. However, RMABs assume the reward function is known. This is unrealistic in many public health settings because patients face unique challenges and it is impossible for a human to know who is most deserving of any intervention at such a large scale. To address this shortcoming, this paper is the first to present the use of inverse reinforcement learning (IRL) to learn desired rewards for RMABs, and we demonstrate improved outcomes in a maternal and child health telehealth program. First we allow public health experts to specify their goals at an aggregate or population level and propose an algorithm to design expert trajectories at scale based on those goals. Second, our algorithm WHIRL uses gradient updates to optimize the objective, allowing for efficient and accurate learning of RMAB rewards. Third, we compare with existing baselines and outperform those in terms of run-time and accuracy. Finally, we evaluate and show the usefulness of WHIRL on thousands on beneficiaries from a real-world maternal and child health setting in India. We publicly release our code here: https://github.com/Gjain234/WHIRL.

Analyzing Human Perceptions of a MEDEVAC Robot in a Simulated Evacuation Scenario

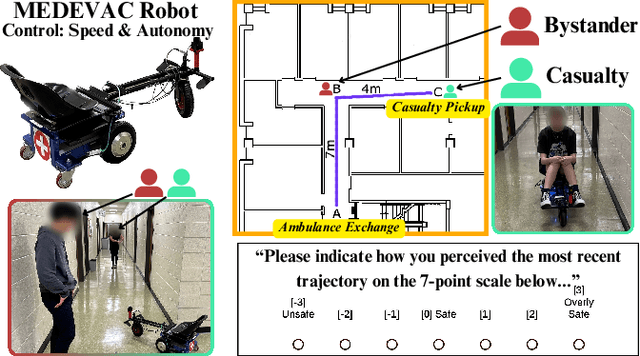
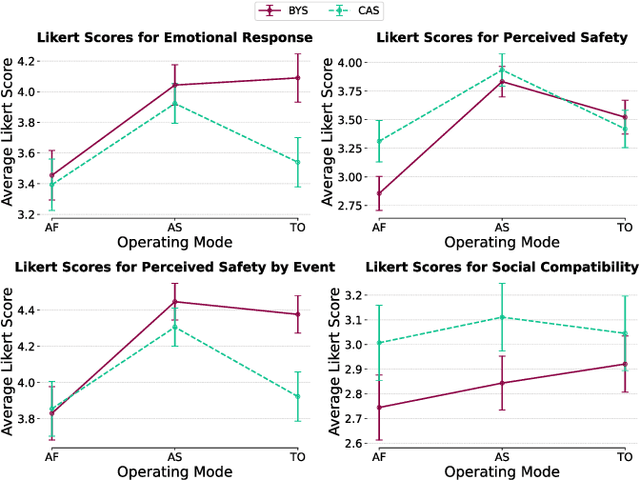
The use of autonomous systems in medical evacuation (MEDEVAC) scenarios is promising, but existing implementations overlook key insights from human-robot interaction (HRI) research. Studies on human-machine teams demonstrate that human perceptions of a machine teammate are critical in governing the machine's performance. Here, we present a mixed factorial design to assess human perceptions of a MEDEVAC robot in a simulated evacuation scenario. Participants were assigned to the role of casualty (CAS) or bystander (BYS) and subjected to three within-subjects conditions based on the MEDEVAC robot's operating mode: autonomous-slow (AS), autonomous-fast (AF), and teleoperation (TO). During each trial, a MEDEVAC robot navigated an 11-meter path, acquiring a casualty and transporting them to an ambulance exchange point while avoiding an idle bystander. Following each trial, subjects completed a questionnaire measuring their emotional states, perceived safety, and social compatibility with the robot. Results indicate a consistent main effect of operating mode on reported emotional states and perceived safety. Pairwise analyses suggest that the employment of the AF operating mode negatively impacted perceptions along these dimensions. There were no persistent differences between casualty and bystander responses.

Open Human-Robot Collaboration using Decentralized Inverse Reinforcement Learning

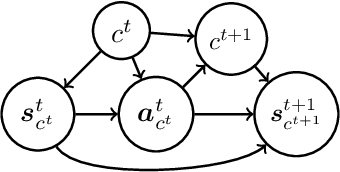
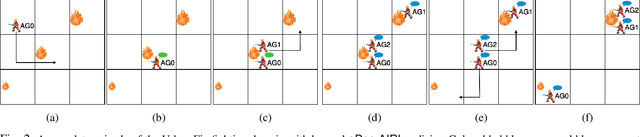
The growing interest in human-robot collaboration (HRC), where humans and robots cooperate towards shared goals, has seen significant advancements over the past decade. While previous research has addressed various challenges, several key issues remain unresolved. Many domains within HRC involve activities that do not necessarily require human presence throughout the entire task. Existing literature typically models HRC as a closed system, where all agents are present for the entire duration of the task. In contrast, an open model offers flexibility by allowing an agent to enter and exit the collaboration as needed, enabling them to concurrently manage other tasks. In this paper, we introduce a novel multiagent framework called oDec-MDP, designed specifically to model open HRC scenarios where agents can join or leave tasks flexibly during execution. We generalize a recent multiagent inverse reinforcement learning method - Dec-AIRL to learn from open systems modeled using the oDec-MDP. Our method is validated through experiments conducted in both a simplified toy firefighting domain and a realistic dyadic human-robot collaborative assembly. Results show that our framework and learning method improves upon its closed system counterpart.

MVSA-Net: Multi-View State-Action Recognition for Robust and Deployable Trajectory Generation

The learn-from-observation (LfO) paradigm is a human-inspired mode for a robot to learn to perform a task simply by watching it being performed. LfO can facilitate robot integration on factory floors by minimizing disruption and reducing tedious programming. A key component of the LfO pipeline is a transformation of the depth camera frames to the corresponding task state and action pairs, which are then relayed to learning techniques such as imitation or inverse reinforcement learning for understanding the task parameters. While several existing computer vision models analyze videos for activity recognition, SA-Net specifically targets robotic LfO from RGB-D data. However, SA-Net and many other models analyze frame data captured from a single viewpoint. Their analysis is therefore highly sensitive to occlusions of the observed task, which are frequent in deployments. An obvious way of reducing occlusions is to simultaneously observe the task from multiple viewpoints and synchronously fuse the multiple streams in the model. Toward this, we present multi-view SA-Net, which generalizes the SA-Net model to allow the perception of multiple viewpoints of the task activity, integrate them, and better recognize the state and action in each frame. Performance evaluations on two distinct domains establish that MVSA-Net recognizes the state-action pairs under occlusion more accurately compared to single-view MVSA-Net and other baselines. Our ablation studies further evaluate its performance under different ambient conditions and establish the contribution of the architecture components. As such, MVSA-Net offers a significantly more robust and deployable state-action trajectory generation compared to previous methods.

A Novel Variational Lower Bound for Inverse Reinforcement Learning

Inverse reinforcement learning (IRL) seeks to learn the reward function from expert trajectories, to understand the task for imitation or collaboration thereby removing the need for manual reward engineering. However, IRL in the context of large, high-dimensional problems with unknown dynamics has been particularly challenging. In this paper, we present a new Variational Lower Bound for IRL (VLB-IRL), which is derived under the framework of a probabilistic graphical model with an optimality node. Our method simultaneously learns the reward function and policy under the learned reward function by maximizing the lower bound, which is equivalent to minimizing the reverse Kullback-Leibler divergence between an approximated distribution of optimality given the reward function and the true distribution of optimality given trajectories. This leads to a new IRL method that learns a valid reward function such that the policy under the learned reward achieves expert-level performance on several known domains. Importantly, the method outperforms the existing state-of-the-art IRL algorithms on these domains by demonstrating better reward from the learned policy.

Latent Interactive A2C for Improved RL in Open Many-Agent Systems

There is a prevalence of multiagent reinforcement learning (MARL) methods that engage in centralized training. But, these methods involve obtaining various types of information from the other agents, which may not be feasible in competitive or adversarial settings. A recent method, the interactive advantage actor critic (IA2C), engages in decentralized training coupled with decentralized execution, aiming to predict the other agents' actions from possibly noisy observations. In this paper, we present the latent IA2C that utilizes an encoder-decoder architecture to learn a latent representation of the hidden state and other agents' actions. Our experiments in two domains -- each populated by many agents -- reveal that the latent IA2C significantly improves sample efficiency by reducing variance and converging faster. Additionally, we introduce open versions of these domains where the agent population may change over time, and evaluate on these instances as well.

IRL with Partial Observations using the Principle of Uncertain Maximum Entropy

The principle of maximum entropy is a broadly applicable technique for computing a distribution with the least amount of information possible while constrained to match empirically estimated feature expectations. However, in many real-world applications that use noisy sensors computing the feature expectations may be challenging due to partial observation of the relevant model variables. For example, a robot performing apprenticeship learning may lose sight of the agent it is learning from due to environmental occlusion. We show that in generalizing the principle of maximum entropy to these types of scenarios we unavoidably introduce a dependency on the learned model to the empirical feature expectations. We introduce the principle of uncertain maximum entropy and present an expectation-maximization based solution generalized from the principle of latent maximum entropy. Finally, we experimentally demonstrate the improved robustness to noisy data offered by our technique in a maximum causal entropy inverse reinforcement learning domain.