The Data-Driven Censored Newsvendor Problem

We study a censored variant of the data-driven newsvendor problem, where the decision-maker must select an ordering quantity that minimizes expected overage and underage costs based only on censored sales data, rather than historical demand realizations. To isolate the impact of demand censoring on this problem, we adopt a distributionally robust optimization framework, evaluating policies according to their worst-case regret over an ambiguity set of distributions. This set is defined by the largest historical order quantity (the observable boundary of the dataset), and contains all distributions matching the true demand distribution up to this boundary, while allowing them to be arbitrary afterwards. We demonstrate a spectrum of achievability under demand censoring by deriving a natural necessary and sufficient condition under which vanishing regret is an achievable goal. In regimes in which it is not, we exactly characterize the information loss due to censoring: an insurmountable lower bound on the performance of any policy, even when the decision-maker has access to infinitely many demand samples. We then leverage these sharp characterizations to propose a natural robust algorithm that adapts to the historical level of demand censoring. We derive finite-sample guarantees for this algorithm across all possible censoring regimes, and show its near-optimality with matching lower bounds (up to polylogarithmic factors). We moreover demonstrate its robust performance via extensive numerical experiments on both synthetic and real-world datasets.

Online Fair Allocation of Perishable Resources

We consider a practically motivated variant of the canonical online fair allocation problem: a decision-maker has a budget of perishable resources to allocate over a fixed number of rounds. Each round sees a random number of arrivals, and the decision-maker must commit to an allocation for these individuals before moving on to the next round. The goal is to construct a sequence of allocations that is envy-free and efficient. Our work makes two important contributions toward this problem: we first derive strong lower bounds on the optimal envy-efficiency trade-off that demonstrate that a decision-maker is fundamentally limited in what she can hope to achieve relative to the no-perishing setting; we then design an algorithm achieving these lower bounds which takes as input $(i)$ a prediction of the perishing order, and $(ii)$ a desired bound on envy. Given the remaining budget in each period, the algorithm uses forecasts of future demand and perishing to adaptively choose one of two carefully constructed guardrail quantities. We demonstrate our algorithm's strong numerical performance - and state-of-the-art, perishing-agnostic algorithms' inefficacy - on simulations calibrated to a real-world dataset.

Earning Sans Learning: Noisy Decision-Making and Labor Supply on Gig Economy Platforms

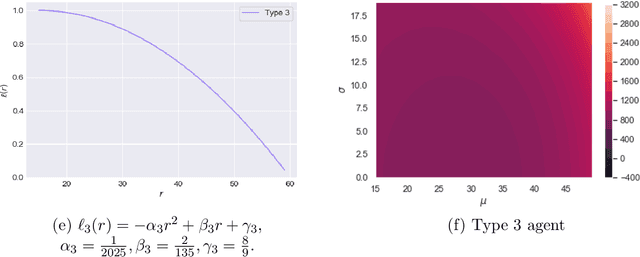
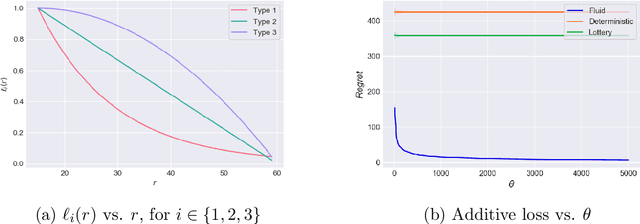
We study a gig economy platform's problem of finding optimal compensation schemes when faced with workers who myopically base their participation decisions on limited information with respect to their earnings. The stylized model we consider captures two key, related features absent from prior work on the operations of on-demand service platforms: (i) workers' lack of information regarding the distribution from which their earnings are drawn and (ii) worker decisions that are sensitive to variability in earnings. Despite its stylized nature, our model induces a complex stochastic optimization problem whose natural fluid relaxation is also a priori intractable. Nevertheless, we uncover a surprising structural property of the relaxation that allows us to design a tractable, fast-converging heuristic policy that is asymptotically optimal amongst the space of all policies that fulfill a fairness property. In doing so, via both theory and extensive simulations, we uncover phenomena that may arise when earnings are volatile and hard to predict, as both the empirical literature and our own data-driven observations suggest may be prevalent on gig economy platforms.