Quantifying the Cost of Learning in Queueing Systems

Queueing systems are widely applicable stochastic models with use cases in communication networks, healthcare, service systems, etc. Although their optimal control has been extensively studied, most existing approaches assume perfect knowledge of system parameters. Of course, this assumption rarely holds in practice where there is parameter uncertainty, thus motivating a recent line of work on bandit learning for queueing systems. This nascent stream of research focuses on the asymptotic performance of the proposed algorithms. In this paper, we argue that an asymptotic metric, which focuses on late-stage performance, is insufficient to capture the intrinsic statistical complexity of learning in queueing systems which typically occurs in the early stage. Instead, we propose the Cost of Learning in Queueing (CLQ), a new metric that quantifies the maximum increase in time-averaged queue length caused by parameter uncertainty. We characterize the CLQ of a single-queue multi-server system, and then extend these results to multi-queue multi-server systems and networks of queues. In establishing our results, we propose a unified analysis framework for CLQ that bridges Lyapunov and bandit analysis, which could be of independent interest.

Towards Practical Robustness Auditing for Linear Regression

We investigate practical algorithms to find or disprove the existence of small subsets of a dataset which, when removed, reverse the sign of a coefficient in an ordinary least squares regression involving that dataset. We empirically study the performance of well-established algorithmic techniques for this task -- mixed integer quadratically constrained optimization for general linear regression problems and exact greedy methods for special cases. We show that these methods largely outperform the state of the art and provide a useful robustness check for regression problems in a few dimensions. However, significant computational bottlenecks remain, especially for the important task of disproving the existence of such small sets of influential samples for regression problems of dimension $3$ or greater. We make some headway on this challenge via a spectral algorithm using ideas drawn from recent innovations in algorithmic robust statistics. We summarize the limitations of known techniques in several challenge datasets to encourage further algorithmic innovation.

Efficient decentralized multi-agent learning in asymmetric queuing systems

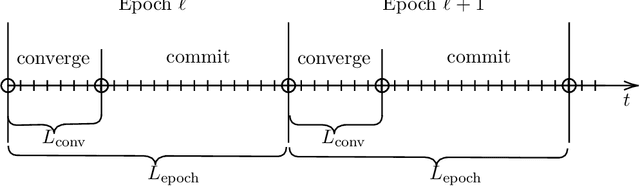
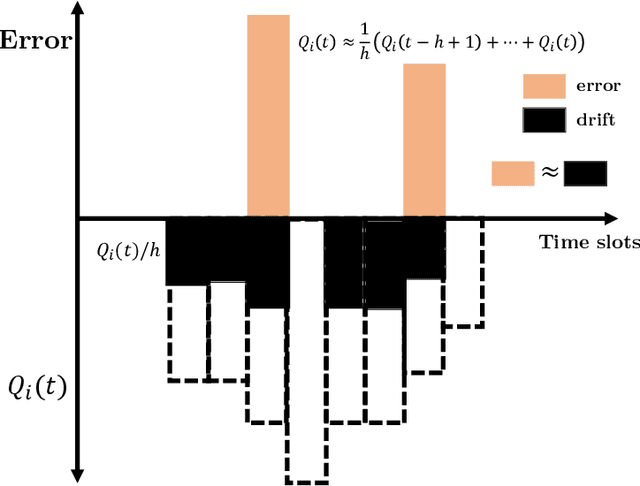
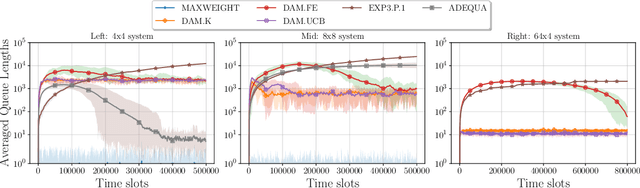
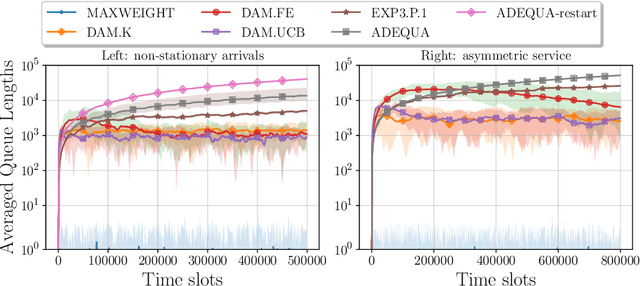
We study decentralized multi-agent learning in bipartite queuing systems, a standard model for service systems. In particular, $N$ agents request service from $K$ servers in a fully decentralized way, i.e, by running the same algorithm without communication. Previous decentralized algorithms are restricted to symmetric systems, have performance that is degrading exponentially in the number of servers, require communication through shared randomness and unique agent identities, and are computationally demanding. In contrast, we provide a simple learning algorithm that, when run decentrally by each agent, leads the queuing system to have efficient performance in general asymmetric bipartite queuing systems while also having additional robustness properties. Along the way, we provide the first UCB-based algorithm for the centralized case of the problem, which resolves an open question by Krishnasamy et al. (2016,2021).

Earning Sans Learning: Noisy Decision-Making and Labor Supply on Gig Economy Platforms

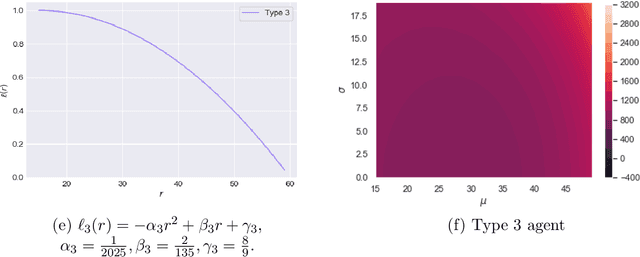
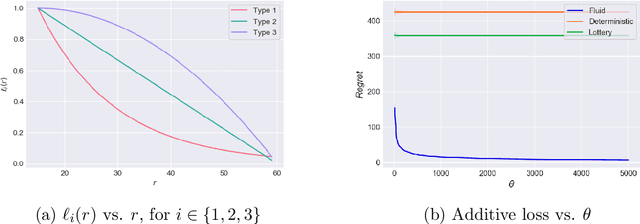
We study a gig economy platform's problem of finding optimal compensation schemes when faced with workers who myopically base their participation decisions on limited information with respect to their earnings. The stylized model we consider captures two key, related features absent from prior work on the operations of on-demand service platforms: (i) workers' lack of information regarding the distribution from which their earnings are drawn and (ii) worker decisions that are sensitive to variability in earnings. Despite its stylized nature, our model induces a complex stochastic optimization problem whose natural fluid relaxation is also a priori intractable. Nevertheless, we uncover a surprising structural property of the relaxation that allows us to design a tractable, fast-converging heuristic policy that is asymptotically optimal amongst the space of all policies that fulfill a fairness property. In doing so, via both theory and extensive simulations, we uncover phenomena that may arise when earnings are volatile and hard to predict, as both the empirical literature and our own data-driven observations suggest may be prevalent on gig economy platforms.