Artificial Replay: A Meta-Algorithm for Harnessing Historical Data in Bandits
Paper and Code
Sep 30, 2022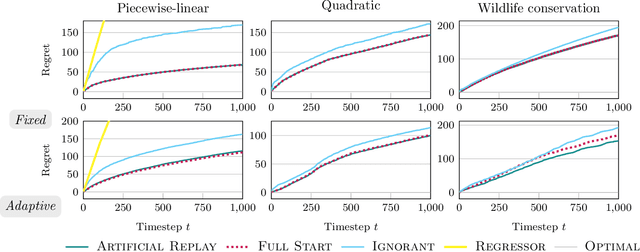

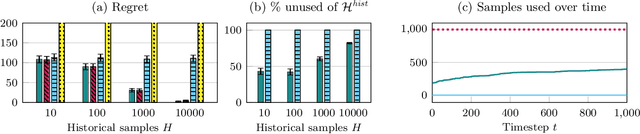
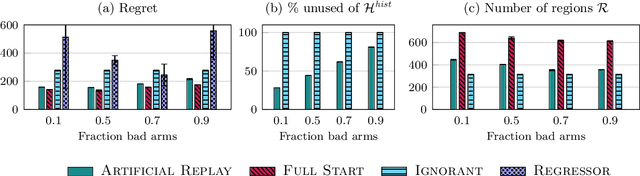
While standard bandit algorithms sometimes incur high regret, their performance can be greatly improved by "warm starting" with historical data. Unfortunately, how best to incorporate historical data is unclear: naively initializing reward estimates using all historical samples can suffer from spurious data and imbalanced data coverage, leading to computational and storage issues - particularly in continuous action spaces. We address these two challenges by proposing Artificial Replay, a meta-algorithm for incorporating historical data into any arbitrary base bandit algorithm. Artificial Replay uses only a subset of the historical data as needed to reduce computation and storage. We show that for a broad class of base algorithms that satisfy independence of irrelevant data (IIData), a novel property that we introduce, our method achieves equal regret as a full warm-start approach while potentially using only a fraction of the historical data. We complement these theoretical results with a case study of $K$-armed and continuous combinatorial bandit algorithms, including on a green security domain using real poaching data, to show the practical benefits of Artificial Replay in achieving optimal regret alongside low computational and storage costs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge