Alankrita Bhatt
Optimal Online Bookmaking for Binary Games
Jan 12, 2025Abstract:In online betting, the bookmaker can update the payoffs it offers on a particular event many times before the event takes place, and the updated payoffs may depend on the bets accumulated thus far. We study the problem of bookmaking with the goal of maximizing the return in the worst-case, with respect to the gamblers' behavior and the event's outcome. We formalize this problem as the \emph{Optimal Online Bookmaking game}, and provide the exact solution for the binary case. To this end, we develop the optimal bookmaking strategy, which relies on a new technique called bi-balancing trees, that assures that the house loss is the same for all \emph{decisive} betting sequences, where the gambler bets all its money on a single outcome in each round.
The SMART approach to instance-optimal online learning
Feb 27, 2024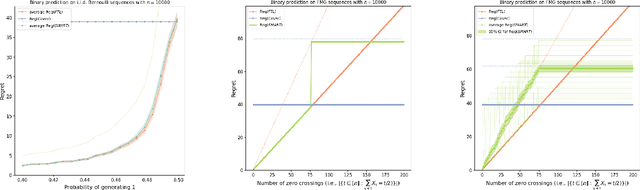
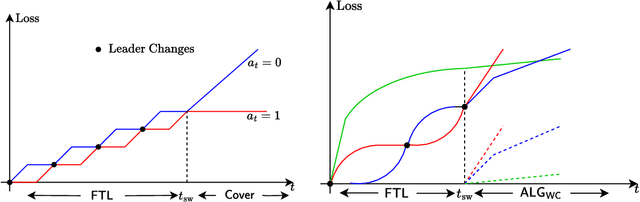
Abstract:We devise an online learning algorithm -- titled Switching via Monotone Adapted Regret Traces (SMART) -- that adapts to the data and achieves regret that is instance optimal, i.e., simultaneously competitive on every input sequence compared to the performance of the follow-the-leader (FTL) policy and the worst case guarantee of any other input policy. We show that the regret of the SMART policy on any input sequence is within a multiplicative factor $e/(e-1) \approx 1.58$ of the smaller of: 1) the regret obtained by FTL on the sequence, and 2) the upper bound on regret guaranteed by the given worst-case policy. This implies a strictly stronger guarantee than typical `best-of-both-worlds' bounds as the guarantee holds for every input sequence regardless of how it is generated. SMART is simple to implement as it begins by playing FTL and switches at most once during the time horizon to the worst-case algorithm. Our approach and results follow from an operational reduction of instance optimal online learning to competitive analysis for the ski-rental problem. We complement our competitive ratio upper bounds with a fundamental lower bound showing that over all input sequences, no algorithm can get better than a $1.43$-fraction of the minimum regret achieved by FTL and the minimax-optimal policy. We also present a modification of SMART that combines FTL with a ``small-loss" algorithm to achieve instance optimality between the regret of FTL and the small loss regret bound.
Smoothed Analysis of Sequential Probability Assignment
Mar 08, 2023Abstract:We initiate the study of smoothed analysis for the sequential probability assignment problem with contexts. We study information-theoretically optimal minmax rates as well as a framework for algorithmic reduction involving the maximum likelihood estimator oracle. Our approach establishes a general-purpose reduction from minimax rates for sequential probability assignment for smoothed adversaries to minimax rates for transductive learning. This leads to optimal (logarithmic) fast rates for parametric classes and classes with finite VC dimension. On the algorithmic front, we develop an algorithm that efficiently taps into the MLE oracle, for general classes of functions. We show that under general conditions this algorithmic approach yields sublinear regret.
Parameter-free Online Linear Optimization with Side Information via Universal Coin Betting
Feb 04, 2022
Abstract:A class of parameter-free online linear optimization algorithms is proposed that harnesses the structure of an adversarial sequence by adapting to some side information. These algorithms combine the reduction technique of Orabona and P{\'a}l (2016) for adapting coin betting algorithms for online linear optimization with universal compression techniques in information theory for incorporating sequential side information to coin betting. Concrete examples are studied in which the side information has a tree structure and consists of quantized values of the previous symbols of the adversarial sequence, including fixed-order and variable-order Markov cases. By modifying the context-tree weighting technique of Willems, Shtarkov, and Tjalkens (1995), the proposed algorithm is further refined to achieve the best performance over all adaptive algorithms with tree-structured side information of a given maximum order in a computationally efficient manner.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge