Contrastive Predictive Coding Done Right for Mutual Information Estimation

The InfoNCE objective, originally introduced for contrastive representation learning, has become a popular choice for mutual information (MI) estimation, despite its indirect connection to MI. In this paper, we demonstrate why InfoNCE should not be regarded as a valid MI estimator, and we introduce a simple modification, which we refer to as InfoNCE-anchor, for accurate MI estimation. Our modification introduces an auxiliary anchor class, enabling consistent density ratio estimation and yielding a plug-in MI estimator with significantly reduced bias. Beyond this, we generalize our framework using proper scoring rules, which recover InfoNCE-anchor as a special case when the log score is employed. This formulation unifies a broad spectrum of contrastive objectives, including NCE, InfoNCE, and $f$-divergence variants, under a single principled framework. Empirically, we find that InfoNCE-anchor with the log score achieves the most accurate MI estimates; however, in self-supervised representation learning experiments, we find that the anchor does not improve the downstream task performance. These findings corroborate that contrastive representation learning benefits not from accurate MI estimation per se, but from the learning of structured density ratios.

Efficient Parametric SVD of Koopman Operator for Stochastic Dynamical Systems

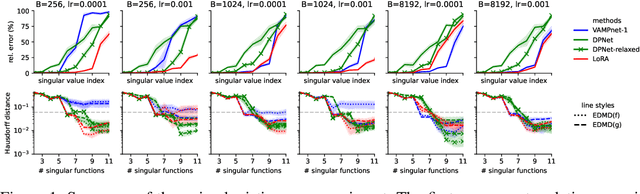
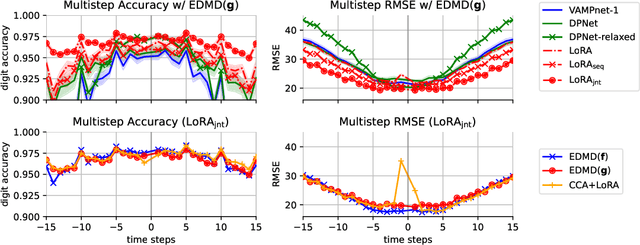
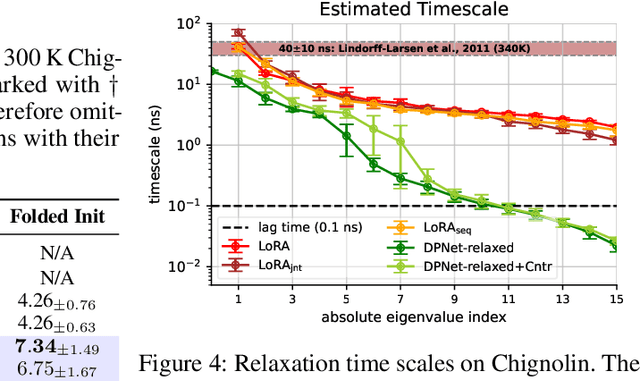
The Koopman operator provides a principled framework for analyzing nonlinear dynamical systems through linear operator theory. Recent advances in dynamic mode decomposition (DMD) have shown that trajectory data can be used to identify dominant modes of a system in a data-driven manner. Building on this idea, deep learning methods such as VAMPnet and DPNet have been proposed to learn the leading singular subspaces of the Koopman operator. However, these methods require backpropagation through potentially numerically unstable operations on empirical second moment matrices, such as singular value decomposition and matrix inversion, during objective computation, which can introduce biased gradient estimates and hinder scalability to large systems. In this work, we propose a scalable and conceptually simple method for learning the top-k singular functions of the Koopman operator for stochastic dynamical systems based on the idea of low-rank approximation. Our approach eliminates the need for unstable linear algebraic operations and integrates easily into modern deep learning pipelines. Empirical results demonstrate that the learned singular subspaces are both reliable and effective for downstream tasks such as eigen-analysis and multi-step prediction.

Score-of-Mixture Training: Training One-Step Generative Models Made Simple

We propose Score-of-Mixture Training (SMT), a novel framework for training one-step generative models by minimizing a class of divergences called the $\alpha$-skew Jensen-Shannon divergence. At its core, SMT estimates the score of mixture distributions between real and fake samples across multiple noise levels. Similar to consistency models, our approach supports both training from scratch (SMT) and distillation using a pretrained diffusion model, which we call Score-of-Mixture Distillation (SMD). It is simple to implement, requires minimal hyperparameter tuning, and ensures stable training. Experiments on CIFAR-10 and ImageNet 64x64 show that SMT/SMD are competitive with and can even outperform existing methods.

A Unified View on Learning Unnormalized Distributions via Noise-Contrastive Estimation

This paper studies a family of estimators based on noise-contrastive estimation (NCE) for learning unnormalized distributions. The main contribution of this work is to provide a unified perspective on various methods for learning unnormalized distributions, which have been independently proposed and studied in separate research communities, through the lens of NCE. This unified view offers new insights into existing estimators. Specifically, for exponential families, we establish the finite-sample convergence rates of the proposed estimators under a set of regularity assumptions, most of which are new.

Improved Evidential Deep Learning via a Mixture of Dirichlet Distributions

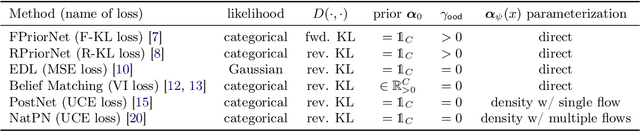
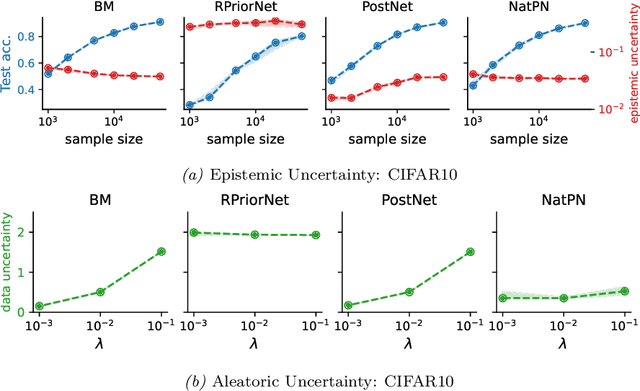
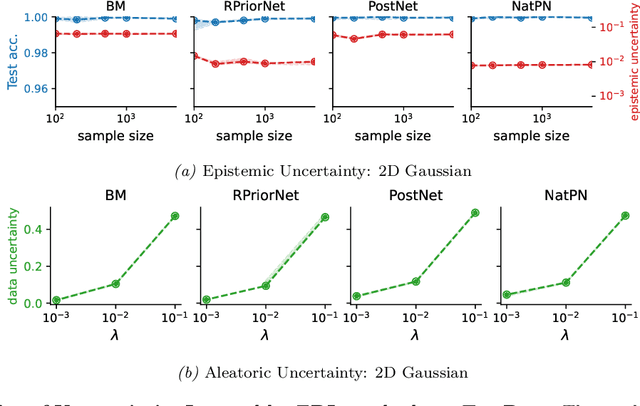
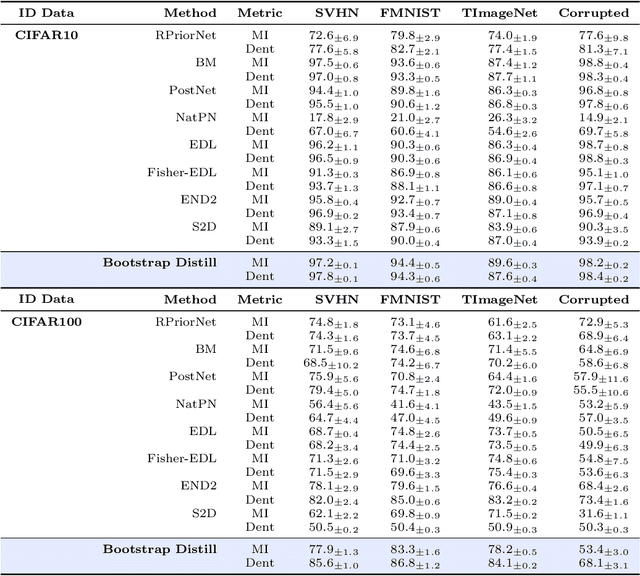
This paper explores a modern predictive uncertainty estimation approach, called evidential deep learning (EDL), in which a single neural network model is trained to learn a meta distribution over the predictive distribution by minimizing a specific objective function. Despite their strong empirical performance, recent studies by Bengs et al. identify a fundamental pitfall of the existing methods: the learned epistemic uncertainty may not vanish even in the infinite-sample limit. We corroborate the observation by providing a unifying view of a class of widely used objectives from the literature. Our analysis reveals that the EDL methods essentially train a meta distribution by minimizing a certain divergence measure between the distribution and a sample-size-independent target distribution, resulting in spurious epistemic uncertainty. Grounded in theoretical principles, we propose learning a consistent target distribution by modeling it with a mixture of Dirichlet distributions and learning via variational inference. Afterward, a final meta distribution model distills the learned uncertainty from the target model. Experimental results across various uncertainty-based downstream tasks demonstrate the superiority of our proposed method, and illustrate the practical implications arising from the consistency and inconsistency of learned epistemic uncertainty.

Operator SVD with Neural Networks via Nested Low-Rank Approximation

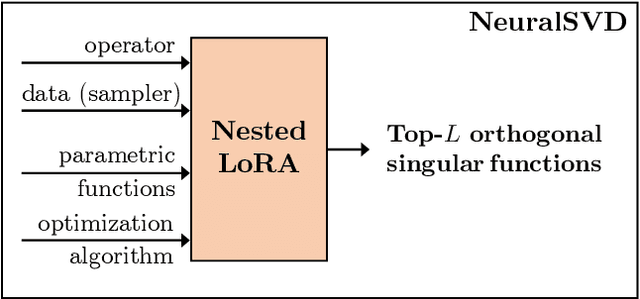
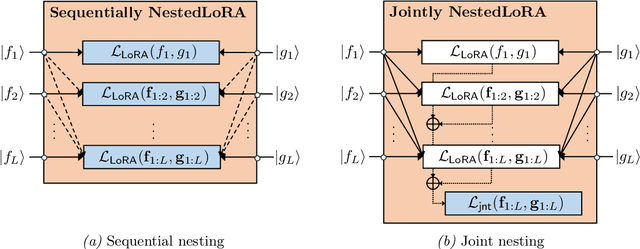
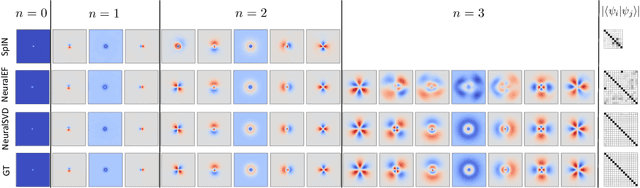
Computing eigenvalue decomposition (EVD) of a given linear operator, or finding its leading eigenvalues and eigenfunctions, is a fundamental task in many machine learning and scientific computing problems. For high-dimensional eigenvalue problems, training neural networks to parameterize the eigenfunctions is considered as a promising alternative to the classical numerical linear algebra techniques. This paper proposes a new optimization framework based on the low-rank approximation characterization of a truncated singular value decomposition, accompanied by new techniques called nesting for learning the top-$L$ singular values and singular functions in the correct order. The proposed method promotes the desired orthogonality in the learned functions implicitly and efficiently via an unconstrained optimization formulation, which is easy to solve with off-the-shelf gradient-based optimization algorithms. We demonstrate the effectiveness of the proposed optimization framework for use cases in computational physics and machine learning.

One-Nearest-Neighbor Search is All You Need for Minimax Optimal Regression and Classification

Recently, Qiao, Duan, and Cheng~(2019) proposed a distributed nearest-neighbor classification method, in which a massive dataset is split into smaller groups, each processed with a $k$-nearest-neighbor classifier, and the final class label is predicted by a majority vote among these groupwise class labels. This paper shows that the distributed algorithm with $k=1$ over a sufficiently large number of groups attains a minimax optimal error rate up to a multiplicative logarithmic factor under some regularity conditions, for both regression and classification problems. Roughly speaking, distributed 1-nearest-neighbor rules with $M$ groups has a performance comparable to standard $\Theta(M)$-nearest-neighbor rules. In the analysis, alternative rules with a refined aggregation method are proposed and shown to attain exact minimax optimal rates.

Parameter-free Online Linear Optimization with Side Information via Universal Coin Betting

A class of parameter-free online linear optimization algorithms is proposed that harnesses the structure of an adversarial sequence by adapting to some side information. These algorithms combine the reduction technique of Orabona and P{\'a}l (2016) for adapting coin betting algorithms for online linear optimization with universal compression techniques in information theory for incorporating sequential side information to coin betting. Concrete examples are studied in which the side information has a tree structure and consists of quantized values of the previous symbols of the adversarial sequence, including fixed-order and variable-order Markov cases. By modifying the context-tree weighting technique of Willems, Shtarkov, and Tjalkens (1995), the proposed algorithm is further refined to achieve the best performance over all adaptive algorithms with tree-structured side information of a given maximum order in a computationally efficient manner.

Feedback Recurrent AutoEncoder

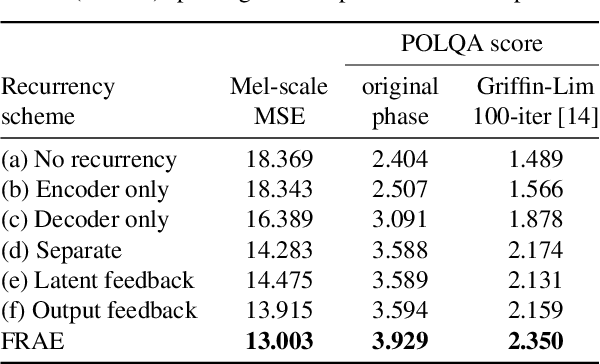
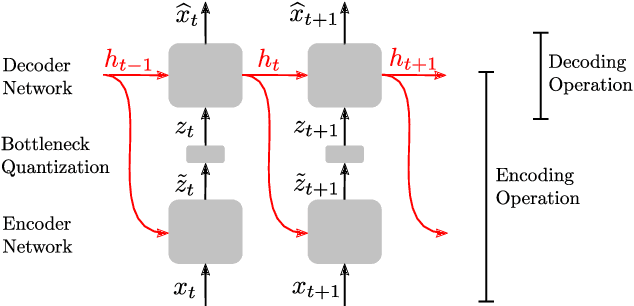
In this work, we propose a new recurrent autoencoder architecture, termed Feedback Recurrent AutoEncoder (FRAE), for online compression of sequential data with temporal dependency. The recurrent structure of FRAE is designed to efficiently extract the redundancy along the time dimension and allows a compact discrete representation of the data to be learned. We demonstrate its effectiveness in speech spectrogram compression. Specifically, we show that the FRAE, paired with a powerful neural vocoder, can produce high-quality speech waveforms at a low, fixed bitrate. We further show that by adding a learned prior for the latent space and using an entropy coder, we can achieve an even lower variable bitrate.

Wyner VAE: Joint and Conditional Generation with Succinct Common Representation Learning

A new variational autoencoder (VAE) model is proposed that learns a succinct common representation of two correlated data variables for conditional and joint generation tasks. The proposed Wyner VAE model is based on two information theoretic problems---distributed simulation and channel synthesis---in which Wyner's common information arises as the fundamental limit of the succinctness of the common representation. The Wyner VAE decomposes a pair of correlated data variables into their common representation (e.g., a shared concept) and local representations that capture the remaining randomness (e.g., texture and style) in respective data variables by imposing the mutual information between the data variables and the common representation as a regularization term. The utility of the proposed approach is demonstrated through experiments for joint and conditional generation with and without style control using synthetic data and real images. Experimental results show that learning a succinct common representation achieves better generative performance and that the proposed model outperforms existing VAE variants and the variational information bottleneck method.