One-Nearest-Neighbor Search is All You Need for Minimax Optimal Regression and Classification

Recently, Qiao, Duan, and Cheng~(2019) proposed a distributed nearest-neighbor classification method, in which a massive dataset is split into smaller groups, each processed with a $k$-nearest-neighbor classifier, and the final class label is predicted by a majority vote among these groupwise class labels. This paper shows that the distributed algorithm with $k=1$ over a sufficiently large number of groups attains a minimax optimal error rate up to a multiplicative logarithmic factor under some regularity conditions, for both regression and classification problems. Roughly speaking, distributed 1-nearest-neighbor rules with $M$ groups has a performance comparable to standard $\Theta(M)$-nearest-neighbor rules. In the analysis, alternative rules with a refined aggregation method are proposed and shown to attain exact minimax optimal rates.

Parameter-free Online Linear Optimization with Side Information via Universal Coin Betting

A class of parameter-free online linear optimization algorithms is proposed that harnesses the structure of an adversarial sequence by adapting to some side information. These algorithms combine the reduction technique of Orabona and P{\'a}l (2016) for adapting coin betting algorithms for online linear optimization with universal compression techniques in information theory for incorporating sequential side information to coin betting. Concrete examples are studied in which the side information has a tree structure and consists of quantized values of the previous symbols of the adversarial sequence, including fixed-order and variable-order Markov cases. By modifying the context-tree weighting technique of Willems, Shtarkov, and Tjalkens (1995), the proposed algorithm is further refined to achieve the best performance over all adaptive algorithms with tree-structured side information of a given maximum order in a computationally efficient manner.

Wyner VAE: Joint and Conditional Generation with Succinct Common Representation Learning

A new variational autoencoder (VAE) model is proposed that learns a succinct common representation of two correlated data variables for conditional and joint generation tasks. The proposed Wyner VAE model is based on two information theoretic problems---distributed simulation and channel synthesis---in which Wyner's common information arises as the fundamental limit of the succinctness of the common representation. The Wyner VAE decomposes a pair of correlated data variables into their common representation (e.g., a shared concept) and local representations that capture the remaining randomness (e.g., texture and style) in respective data variables by imposing the mutual information between the data variables and the common representation as a regularization term. The utility of the proposed approach is demonstrated through experiments for joint and conditional generation with and without style control using synthetic data and real images. Experimental results show that learning a succinct common representation achieves better generative performance and that the proposed model outperforms existing VAE variants and the variational information bottleneck method.

Nearest neighbor density functional estimation based on inverse Laplace transform

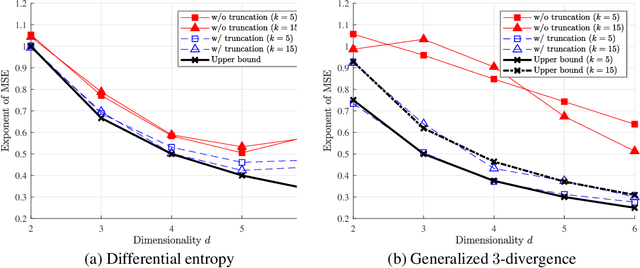
A general approach to $L_2$-consistent estimation of various density functionals using $k$-nearest neighbor distances is proposed, along with the analysis of convergence rates in mean squared error. The construction of the estimator is based on inverse Laplace transforms related to the target density functional, which arises naturally from the convergence of a normalized volume of $k$-nearest neighbor ball to a Gamma distribution in the sample limit. Some instantiations of the proposed estimator rediscover existing $k$-nearest neighbor based estimators of Shannon and Renyi entropies and Kullback--Leibler and Renyi divergences, and discover new consistent estimators for many other functionals, such as Jensen--Shannon divergence and generalized entropies and divergences. A unified finite-sample analysis of the proposed estimator is presented that builds on a recent result by Gao, Oh, and Viswanath (2017) on the finite sample behavior of the Kozachenko--Leoneko estimator of entropy.

Energy-Based Sequence GANs for Recommendation and Their Connection to Imitation Learning

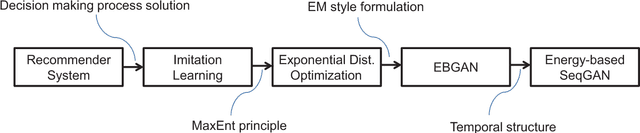
Recommender systems aim to find an accurate and efficient mapping from historic data of user-preferred items to a new item that is to be liked by a user. Towards this goal, energy-based sequence generative adversarial nets (EB-SeqGANs) are adopted for recommendation by learning a generative model for the time series of user-preferred items. By recasting the energy function as the feature function, the proposed EB-SeqGANs is interpreted as an instance of maximum-entropy imitation learning.