Gregory W. Wornell
LegacyAvatars: Volumetric Face Avatars For Traditional Graphics Pipelines
Jan 18, 2026Abstract:We introduce a novel representation for efficient classical rendering of photorealistic 3D face avatars. Leveraging recent advances in radiance fields anchored to parametric face models, our approach achieves controllable volumetric rendering of complex facial features, including hair, skin, and eyes. At enrollment time, we learn a set of radiance manifolds in 3D space to extract an explicit layered mesh, along with appearance and warp textures. During deployment, this allows us to control and animate the face through simple linear blending and alpha compositing of textures over a static mesh. This explicit representation also enables the generated avatar to be efficiently streamed online and then rendered using classical mesh and shader-based rendering on legacy graphics platforms, eliminating the need for any custom engineering or integration.
Contrastive Predictive Coding Done Right for Mutual Information Estimation
Oct 29, 2025Abstract:The InfoNCE objective, originally introduced for contrastive representation learning, has become a popular choice for mutual information (MI) estimation, despite its indirect connection to MI. In this paper, we demonstrate why InfoNCE should not be regarded as a valid MI estimator, and we introduce a simple modification, which we refer to as InfoNCE-anchor, for accurate MI estimation. Our modification introduces an auxiliary anchor class, enabling consistent density ratio estimation and yielding a plug-in MI estimator with significantly reduced bias. Beyond this, we generalize our framework using proper scoring rules, which recover InfoNCE-anchor as a special case when the log score is employed. This formulation unifies a broad spectrum of contrastive objectives, including NCE, InfoNCE, and $f$-divergence variants, under a single principled framework. Empirically, we find that InfoNCE-anchor with the log score achieves the most accurate MI estimates; however, in self-supervised representation learning experiments, we find that the anchor does not improve the downstream task performance. These findings corroborate that contrastive representation learning benefits not from accurate MI estimation per se, but from the learning of structured density ratios.
Efficient Parametric SVD of Koopman Operator for Stochastic Dynamical Systems
Jul 09, 2025
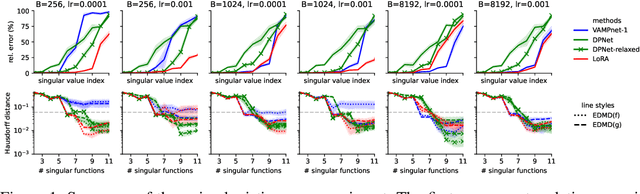
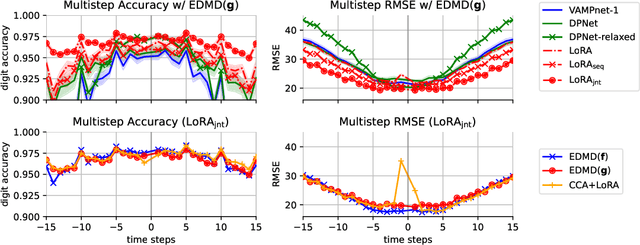
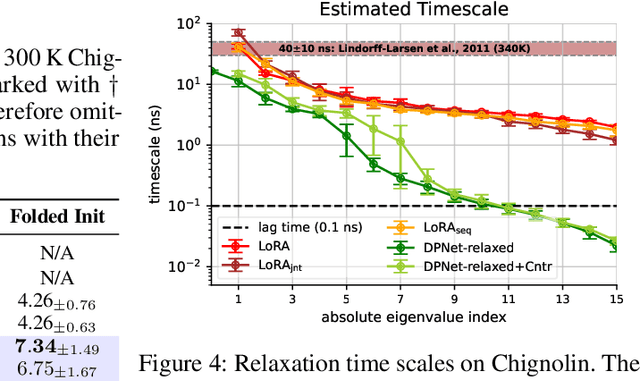
Abstract:The Koopman operator provides a principled framework for analyzing nonlinear dynamical systems through linear operator theory. Recent advances in dynamic mode decomposition (DMD) have shown that trajectory data can be used to identify dominant modes of a system in a data-driven manner. Building on this idea, deep learning methods such as VAMPnet and DPNet have been proposed to learn the leading singular subspaces of the Koopman operator. However, these methods require backpropagation through potentially numerically unstable operations on empirical second moment matrices, such as singular value decomposition and matrix inversion, during objective computation, which can introduce biased gradient estimates and hinder scalability to large systems. In this work, we propose a scalable and conceptually simple method for learning the top-k singular functions of the Koopman operator for stochastic dynamical systems based on the idea of low-rank approximation. Our approach eliminates the need for unstable linear algebraic operations and integrates easily into modern deep learning pipelines. Empirical results demonstrate that the learned singular subspaces are both reliable and effective for downstream tasks such as eigen-analysis and multi-step prediction.
Extremum Encoding for Joint Baseband Signal Compression and Time-Delay Estimation for Distributed Systems
Dec 24, 2024Abstract:The ubiquitous time-delay estimation (TDE) problem becomes nontrivial when sensors are non-co-located and communication between them is limited. Building on the recently proposed "extremum encoding" compression-estimation scheme, we address the critical extension to complex-valued signals, suitable for radio-frequency (RF) baseband processing. This extension introduces new challenges, e.g., due to unknown phase of the signal of interest and random phase of the noise, rendering a na\"ive application of the original scheme inapplicable and irrelevant. In the face of these challenges, we propose a judiciously adapted, though natural, extension of the scheme, paving its way to RF applications. While our extension leads to a different statistical analysis, including extremes of non-Gaussian distributions, we show that, ultimately, its asymptotic behavior is akin to the original scheme. We derive an exponentially tight upper bound on its error probability, corroborate our results via simulation experiments, and demonstrate the superior performance compared to two benchmark approaches.
Estimating the Number and Locations of Boundaries in Reverberant Environments with Deep Learning
Nov 04, 2024



Abstract:Underwater acoustic environment estimation is a challenging but important task for remote sensing scenarios. Current estimation methods require high signal strength and a solution to the fragile echo labeling problem to be effective. In previous publications, we proposed a general deep learning-based method for two-dimensional environment estimation which outperformed the state-of-the-art, both in simulation and in real-life experimental settings. A limitation of this method was that some prior information had to be provided by the user on the number and locations of the reflective boundaries, and that its neural networks had to be re-trained accordingly for different environments. Utilizing more advanced neural network and time delay estimation techniques, the proposed improved method no longer requires prior knowledge the number of boundaries or their locations, and is able to estimate two-dimensional environments with one or two boundaries. Future work will extend the proposed method to more boundaries and larger-scale environments.
A Unified View on Learning Unnormalized Distributions via Noise-Contrastive Estimation
Sep 26, 2024Abstract:This paper studies a family of estimators based on noise-contrastive estimation (NCE) for learning unnormalized distributions. The main contribution of this work is to provide a unified perspective on various methods for learning unnormalized distributions, which have been independently proposed and studied in separate research communities, through the lens of NCE. This unified view offers new insights into existing estimators. Specifically, for exponential families, we establish the finite-sample convergence rates of the proposed estimators under a set of regularity assumptions, most of which are new.
RF Challenge: The Data-Driven Radio Frequency Signal Separation Challenge
Sep 13, 2024



Abstract:This paper addresses the critical problem of interference rejection in radio-frequency (RF) signals using a novel, data-driven approach that leverages state-of-the-art AI models. Traditionally, interference rejection algorithms are manually tailored to specific types of interference. This work introduces a more scalable data-driven solution and contains the following contributions. First, we present an insightful signal model that serves as a foundation for developing and analyzing interference rejection algorithms. Second, we introduce the RF Challenge, a publicly available dataset featuring diverse RF signals along with code templates, which facilitates data-driven analysis of RF signal problems. Third, we propose novel AI-based rejection algorithms, specifically architectures like UNet and WaveNet, and evaluate their performance across eight different signal mixture types. These models demonstrate superior performance exceeding traditional methods like matched filtering and linear minimum mean square error estimation by up to two orders of magnitude in bit-error rate. Fourth, we summarize the results from an open competition hosted at 2024 IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP 2024) based on the RF Challenge, highlighting the significant potential for continued advancements in this area. Our findings underscore the promise of deep learning algorithms in mitigating interference, offering a strong foundation for future research.
FaceFolds: Meshed Radiance Manifolds for Efficient Volumetric Rendering of Dynamic Faces
Apr 22, 2024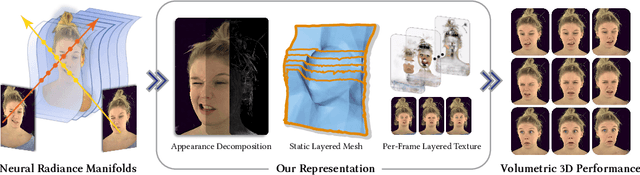

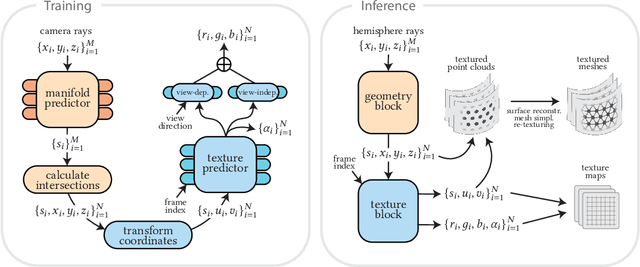
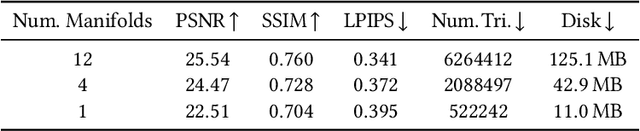
Abstract:3D rendering of dynamic face captures is a challenging problem, and it demands improvements on several fronts$\unicode{x2014}$photorealism, efficiency, compatibility, and configurability. We present a novel representation that enables high-quality volumetric rendering of an actor's dynamic facial performances with minimal compute and memory footprint. It runs natively on commodity graphics soft- and hardware, and allows for a graceful trade-off between quality and efficiency. Our method utilizes recent advances in neural rendering, particularly learning discrete radiance manifolds to sparsely sample the scene to model volumetric effects. We achieve efficient modeling by learning a single set of manifolds for the entire dynamic sequence, while implicitly modeling appearance changes as temporal canonical texture. We export a single layered mesh and view-independent RGBA texture video that is compatible with legacy graphics renderers without additional ML integration. We demonstrate our method by rendering dynamic face captures of real actors in a game engine, at comparable photorealism to state-of-the-art neural rendering techniques at previously unseen frame rates.
A Joint Data Compression and Time-Delay Estimation Method For Distributed Systems via Extremum Encoding
Apr 14, 2024Abstract:Motivated by the proliferation of mobile devices, we consider a basic form of the ubiquitous problem of time-delay estimation (TDE), but with communication constraints between two non co-located sensors. In this setting, when joint processing of the received signals is not possible, a compression technique that is tailored to TDE is desirable. For our basic TDE formulation, we develop such a joint compression-estimation strategy based on the notion of what we term "extremum encoding", whereby we send the index of the maximum of a finite-length time-series from one sensor to another. Subsequent joint processing of the encoded message with locally observed data gives rise to our proposed time-delay "maximum-index"-based estimator. We derive an exponentially tight upper bound on its error probability, establishing its consistency with respect to the number of transmitted bits. We further validate our analysis via simulations, and comment on potential extensions and generalizations of the basic methodology.
Improved Evidential Deep Learning via a Mixture of Dirichlet Distributions
Feb 09, 2024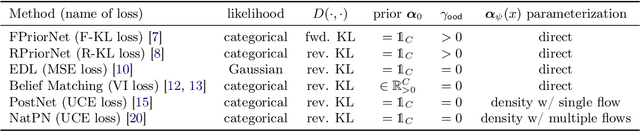
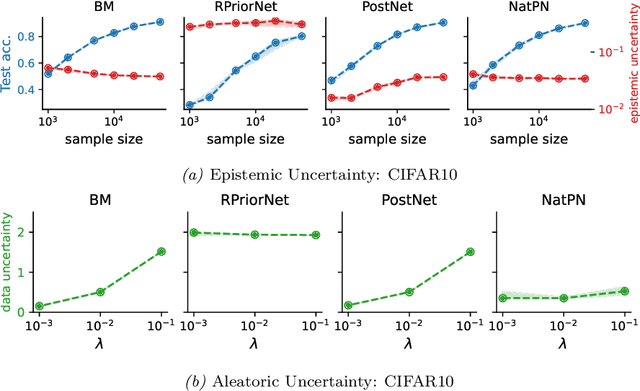
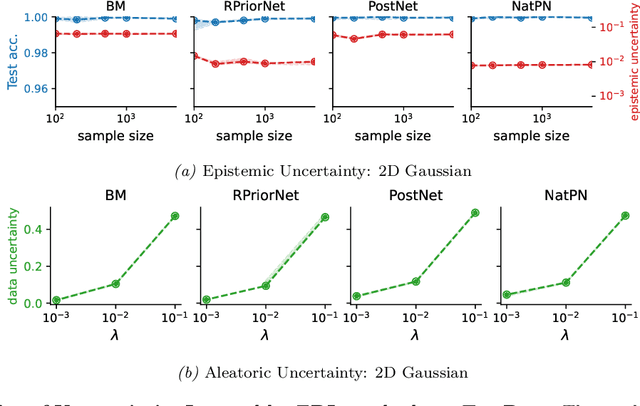
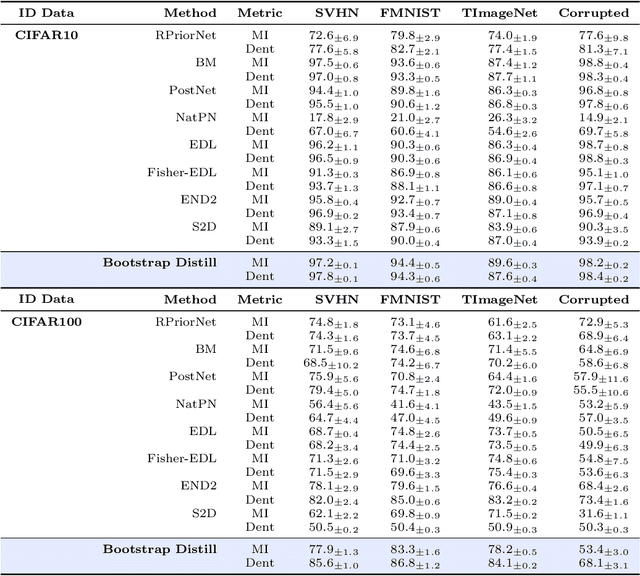
Abstract:This paper explores a modern predictive uncertainty estimation approach, called evidential deep learning (EDL), in which a single neural network model is trained to learn a meta distribution over the predictive distribution by minimizing a specific objective function. Despite their strong empirical performance, recent studies by Bengs et al. identify a fundamental pitfall of the existing methods: the learned epistemic uncertainty may not vanish even in the infinite-sample limit. We corroborate the observation by providing a unifying view of a class of widely used objectives from the literature. Our analysis reveals that the EDL methods essentially train a meta distribution by minimizing a certain divergence measure between the distribution and a sample-size-independent target distribution, resulting in spurious epistemic uncertainty. Grounded in theoretical principles, we propose learning a consistent target distribution by modeling it with a mixture of Dirichlet distributions and learning via variational inference. Afterward, a final meta distribution model distills the learned uncertainty from the target model. Experimental results across various uncertainty-based downstream tasks demonstrate the superiority of our proposed method, and illustrate the practical implications arising from the consistency and inconsistency of learned epistemic uncertainty.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge