Distributional Information Embedding: A Framework for Multi-bit Watermarking

This paper introduces a novel problem, distributional information embedding, motivated by the practical demands of multi-bit watermarking for large language models (LLMs). Unlike traditional information embedding, which embeds information into a pre-existing host signal, LLM watermarking actively controls the text generation process--adjusting the token distribution--to embed a detectable signal. We develop an information-theoretic framework to analyze this distributional information embedding problem, characterizing the fundamental trade-offs among three critical performance metrics: text quality, detectability, and information rate. In the asymptotic regime, we demonstrate that the maximum achievable rate with vanishing error corresponds to the entropy of the LLM's output distribution and increases with higher allowable distortion. We also characterize the optimal watermarking scheme to achieve this rate. Extending the analysis to the finite-token case, we identify schemes that maximize detection probability while adhering to constraints on false alarm and distortion.

Image Watermarks are Removable Using Controllable Regeneration from Clean Noise

Image watermark techniques provide an effective way to assert ownership, deter misuse, and trace content sources, which has become increasingly essential in the era of large generative models. A critical attribute of watermark techniques is their robustness against various manipulations. In this paper, we introduce a watermark removal approach capable of effectively nullifying the state of the art watermarking techniques. Our primary insight involves regenerating the watermarked image starting from a clean Gaussian noise via a controllable diffusion model, utilizing the extracted semantic and spatial features from the watermarked image. The semantic control adapter and the spatial control network are specifically trained to control the denoising process towards ensuring image quality and enhancing consistency between the cleaned image and the original watermarked image. To achieve a smooth trade-off between watermark removal performance and image consistency, we further propose an adjustable and controllable regeneration scheme. This scheme adds varying numbers of noise steps to the latent representation of the watermarked image, followed by a controlled denoising process starting from this noisy latent representation. As the number of noise steps increases, the latent representation progressively approaches clean Gaussian noise, facilitating the desired trade-off. We apply our watermark removal methods across various watermarking techniques, and the results demonstrate that our methods offer superior visual consistency/quality and enhanced watermark removal performance compared to existing regeneration approaches.

Universally Optimal Watermarking Schemes for LLMs: from Theory to Practice

Large Language Models (LLMs) boosts human efficiency but also poses misuse risks, with watermarking serving as a reliable method to differentiate AI-generated content from human-created text. In this work, we propose a novel theoretical framework for watermarking LLMs. Particularly, we jointly optimize both the watermarking scheme and detector to maximize detection performance, while controlling the worst-case Type-I error and distortion in the watermarked text. Within our framework, we characterize the universally minimum Type-II error, showing a fundamental trade-off between detection performance and distortion. More importantly, we identify the optimal type of detectors and watermarking schemes. Building upon our theoretical analysis, we introduce a practical, model-agnostic and computationally efficient token-level watermarking algorithm that invokes a surrogate model and the Gumbel-max trick. Empirical results on Llama-13B and Mistral-8$\times$7B demonstrate the effectiveness of our method. Furthermore, we also explore how robustness can be integrated into our theoretical framework, which provides a foundation for designing future watermarking systems with improved resilience to adversarial attacks.

SAUC: Sparsity-Aware Uncertainty Calibration for Spatiotemporal Prediction with Graph Neural Networks

Quantifying uncertainty is crucial for robust and reliable predictions. However, existing spatiotemporal deep learning mostly focuses on deterministic prediction, overlooking the inherent uncertainty in such prediction. Particularly, highly-granular spatiotemporal datasets are often sparse, posing extra challenges in prediction and uncertainty quantification. To address these issues, this paper introduces a novel post-hoc Sparsity-awar Uncertainty Calibration (SAUC) framework, which calibrates uncertainty in both zero and non-zero values. To develop SAUC, we firstly modify the state-of-the-art deterministic spatiotemporal Graph Neural Networks (ST-GNNs) to probabilistic ones in the pre-calibration phase. Then we calibrate the probabilistic ST-GNNs for zero and non-zero values using quantile approaches.Through extensive experiments, we demonstrate that SAUC can effectively fit the variance of sparse data and generalize across two real-world spatiotemporal datasets at various granularities. Specifically, our empirical experiments show a 20\% reduction in calibration errors in zero entries on the sparse traffic accident and urban crime prediction. Overall, this work demonstrates the theoretical and empirical values of the SAUC framework, thus bridging a significant gap between uncertainty quantification and spatiotemporal prediction.

Improved Evidential Deep Learning via a Mixture of Dirichlet Distributions

This paper explores a modern predictive uncertainty estimation approach, called evidential deep learning (EDL), in which a single neural network model is trained to learn a meta distribution over the predictive distribution by minimizing a specific objective function. Despite their strong empirical performance, recent studies by Bengs et al. identify a fundamental pitfall of the existing methods: the learned epistemic uncertainty may not vanish even in the infinite-sample limit. We corroborate the observation by providing a unifying view of a class of widely used objectives from the literature. Our analysis reveals that the EDL methods essentially train a meta distribution by minimizing a certain divergence measure between the distribution and a sample-size-independent target distribution, resulting in spurious epistemic uncertainty. Grounded in theoretical principles, we propose learning a consistent target distribution by modeling it with a mixture of Dirichlet distributions and learning via variational inference. Afterward, a final meta distribution model distills the learned uncertainty from the target model. Experimental results across various uncertainty-based downstream tasks demonstrate the superiority of our proposed method, and illustrate the practical implications arising from the consistency and inconsistency of learned epistemic uncertainty.

Operator SVD with Neural Networks via Nested Low-Rank Approximation

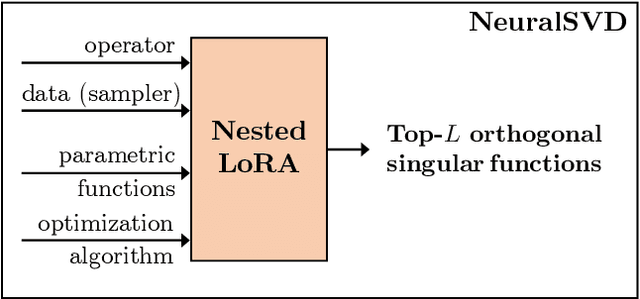
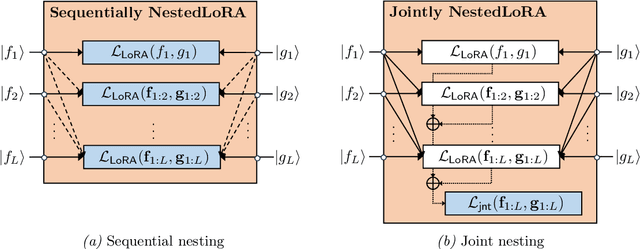
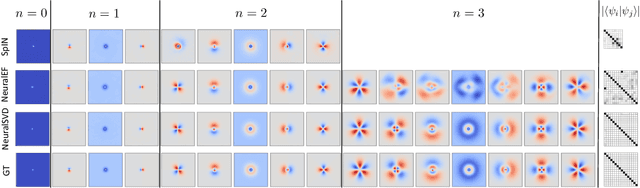
Computing eigenvalue decomposition (EVD) of a given linear operator, or finding its leading eigenvalues and eigenfunctions, is a fundamental task in many machine learning and scientific computing problems. For high-dimensional eigenvalue problems, training neural networks to parameterize the eigenfunctions is considered as a promising alternative to the classical numerical linear algebra techniques. This paper proposes a new optimization framework based on the low-rank approximation characterization of a truncated singular value decomposition, accompanied by new techniques called nesting for learning the top-$L$ singular values and singular functions in the correct order. The proposed method promotes the desired orthogonality in the learned functions implicitly and efficiently via an unconstrained optimization formulation, which is easy to solve with off-the-shelf gradient-based optimization algorithms. We demonstrate the effectiveness of the proposed optimization framework for use cases in computational physics and machine learning.

Adaptive Text Watermark for Large Language Models

The advancement of Large Language Models (LLMs) has led to increasing concerns about the misuse of AI-generated text, and watermarking for LLM-generated text has emerged as a potential solution. However, it is challenging to generate high-quality watermarked text while maintaining strong security, robustness, and the ability to detect watermarks without prior knowledge of the prompt or model. This paper proposes an adaptive watermarking strategy to address this problem. To improve the text quality and maintain robustness, we adaptively add watermarking to token distributions with high entropy measured using an auxiliary model and keep the low entropy token distributions untouched. For the sake of security and to further minimize the watermark's impact on text quality, instead of using a fixed green/red list generated from a random secret key, which can be vulnerable to decryption and forgery, we adaptively scale up the output logits in proportion based on the semantic embedding of previously generated text using a well designed semantic mapping model. Our experiments involving various LLMs demonstrate that our approach achieves comparable robustness performance to existing watermark methods. Additionally, the text generated by our method has perplexity comparable to that of \emph{un-watermarked} LLMs while maintaining security even under various attacks.

Class-wise Generalization Error: an Information-Theoretic Analysis

Existing generalization theories of supervised learning typically take a holistic approach and provide bounds for the expected generalization over the whole data distribution, which implicitly assumes that the model generalizes similarly for all the classes. In practice, however, there are significant variations in generalization performance among different classes, which cannot be captured by the existing generalization bounds. In this work, we tackle this problem by theoretically studying the class-generalization error, which quantifies the generalization performance of each individual class. We derive a novel information-theoretic bound for class-generalization error using the KL divergence, and we further obtain several tighter bounds using the conditional mutual information (CMI), which are significantly easier to estimate in practice. We empirically validate our proposed bounds in different neural networks and show that they accurately capture the complex class-generalization error behavior. Moreover, we show that the theoretical tools developed in this paper can be applied in several applications beyond this context.

SGLD-Based Information Criteria and the Over-Parameterized Regime

Double-descent refers to the unexpected drop in test loss of a learning algorithm beyond an interpolating threshold with over-parameterization, which is not predicted by information criteria in their classical forms due to the limitations in the standard asymptotic approach. We update these analyses using the information risk minimization framework and provide Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) for models learned by stochastic gradient Langevin dynamics (SGLD). Notably, the AIC and BIC penalty terms for SGLD correspond to specific information measures, i.e., symmetrized KL information and KL divergence. We extend this information-theoretic analysis to over-parameterized models by characterizing the SGLD-based BIC for the random feature model in the regime where the number of parameters $p$ and the number of samples $n$ tend to infinity, with $p/n$ fixed. Our experiments demonstrate that the refined SGLD-based BIC can track the double-descent curve, providing meaningful guidance for model selection and revealing new insights into the behavior of SGLD learning algorithms in the over-parameterized regime.

Feature Learning in Image Hierarchies using Functional Maximal Correlation

This paper proposes the Hierarchical Functional Maximal Correlation Algorithm (HFMCA), a hierarchical methodology that characterizes dependencies across two hierarchical levels in multiview systems. By framing view similarities as dependencies and ensuring contrastivity by imposing orthonormality, HFMCA achieves faster convergence and increased stability in self-supervised learning. HFMCA defines and measures dependencies within image hierarchies, from pixels and patches to full images. We find that the network topology for approximating orthonormal basis functions aligns with a vanilla CNN, enabling the decomposition of density ratios between neighboring layers of feature maps. This approach provides powerful interpretability, revealing the resemblance between supervision and self-supervision through the lens of internal representations.