Pixel-Wise Color Constancy via Smoothness Techniques in Multi-Illuminant Scenes

Most scenes are illuminated by several light sources, where the traditional assumption of uniform illumination is invalid. This issue is ignored in most color constancy methods, primarily due to the complex spatial impact of multiple light sources on the image. Moreover, most existing multi-illuminant methods fail to preserve the smooth change of illumination, which stems from spatial dependencies in natural images. Motivated by this, we propose a novel multi-illuminant color constancy method, by learning pixel-wise illumination maps caused by multiple light sources. The proposed method enforces smoothness within neighboring pixels, by regularizing the training with the total variation loss. Moreover, a bilateral filter is provisioned further to enhance the natural appearance of the estimated images, while preserving the edges. Additionally, we propose a label-smoothing technique that enables the model to generalize well despite the uncertainties in ground truth. Quantitative and qualitative experiments demonstrate that the proposed method outperforms the state-of-the-art.

Class-wise Generalization Error: an Information-Theoretic Analysis

Existing generalization theories of supervised learning typically take a holistic approach and provide bounds for the expected generalization over the whole data distribution, which implicitly assumes that the model generalizes similarly for all the classes. In practice, however, there are significant variations in generalization performance among different classes, which cannot be captured by the existing generalization bounds. In this work, we tackle this problem by theoretically studying the class-generalization error, which quantifies the generalization performance of each individual class. We derive a novel information-theoretic bound for class-generalization error using the KL divergence, and we further obtain several tighter bounds using the conditional mutual information (CMI), which are significantly easier to estimate in practice. We empirically validate our proposed bounds in different neural networks and show that they accurately capture the complex class-generalization error behavior. Moreover, we show that the theoretical tools developed in this paper can be applied in several applications beyond this context.

Newton Method-based Subspace Support Vector Data Description

In this paper, we present an adaptation of Newton's method for the optimization of Subspace Support Vector Data Description (S-SVDD). The objective of S-SVDD is to map the original data to a subspace optimized for one-class classification, and the iterative optimization process of data mapping and description in S-SVDD relies on gradient descent. However, gradient descent only utilizes first-order information, which may lead to suboptimal results. To address this limitation, we leverage Newton's method to enhance data mapping and data description for an improved optimization of subspace learning-based one-class classification. By incorporating this auxiliary information, Newton's method offers a more efficient strategy for subspace learning in one-class classification as compared to gradient-based optimization. The paper discusses the limitations of gradient descent and the advantages of using Newton's method in subspace learning for one-class classification tasks. We provide both linear and nonlinear formulations of Newton's method-based optimization for S-SVDD. In our experiments, we explored both the minimization and maximization strategies of the objective. The results demonstrate that the proposed optimization strategy outperforms the gradient-based S-SVDD in most cases.

Convolutional autoencoder-based multimodal one-class classification

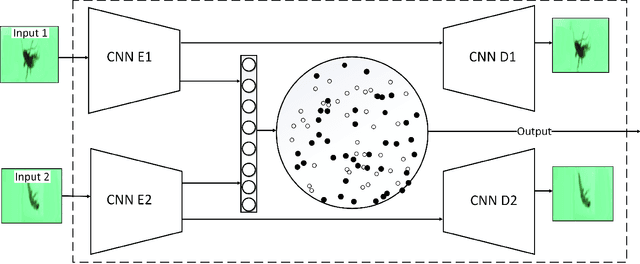
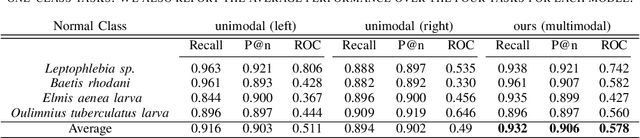
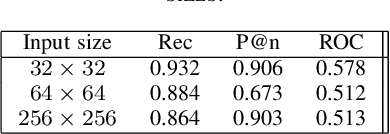
One-class classification refers to approaches of learning using data from a single class only. In this paper, we propose a deep learning one-class classification method suitable for multimodal data, which relies on two convolutional autoencoders jointly trained to reconstruct the positive input data while obtaining the data representations in the latent space as compact as possible. During inference, the distance of the latent representation of an input to the origin can be used as an anomaly score. Experimental results using a multimodal macroinvertebrate image classification dataset show that the proposed multimodal method yields better results as compared to the unimodal approach. Furthermore, study the effect of different input image sizes, and we investigate how recently proposed feature diversity regularizers affect the performance of our approach. We show that such regularizers improve performance.

On Feature Diversity in Energy-based Models

Energy-based learning is a powerful learning paradigm that encapsulates various discriminative and generative approaches. An energy-based model (EBM) is typically formed of inner-model(s) that learn a combination of the different features to generate an energy mapping for each input configuration. In this paper, we focus on the diversity of the produced feature set. We extend the probably approximately correct (PAC) theory of EBMs and analyze the effect of redundancy reduction on the performance of EBMs. We derive generalization bounds for various learning contexts, i.e., regression, classification, and implicit regression, with different energy functions and we show that indeed reducing redundancy of the feature set can consistently decrease the gap between the true and empirical expectation of the energy and boosts the performance of the model.

WLD-Reg: A Data-dependent Within-layer Diversity Regularizer

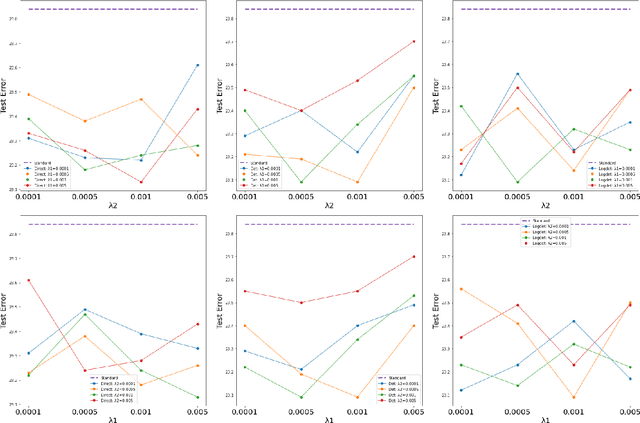
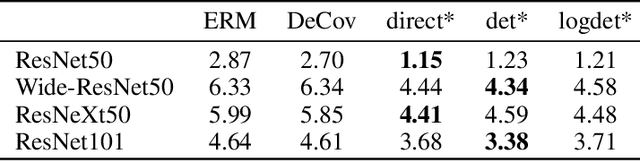
Neural networks are composed of multiple layers arranged in a hierarchical structure jointly trained with a gradient-based optimization, where the errors are back-propagated from the last layer back to the first one. At each optimization step, neurons at a given layer receive feedback from neurons belonging to higher layers of the hierarchy. In this paper, we propose to complement this traditional 'between-layer' feedback with additional 'within-layer' feedback to encourage the diversity of the activations within the same layer. To this end, we measure the pairwise similarity between the outputs of the neurons and use it to model the layer's overall diversity. We present an extensive empirical study confirming that the proposed approach enhances the performance of several state-of-the-art neural network models in multiple tasks. The code is publically available at \url{https://github.com/firasl/AAAI-23-WLD-Reg}

Efficient CNN with uncorrelated Bag of Features pooling

Despite the superior performance of CNN, deploying them on low computational power devices is still limited as they are typically computationally expensive. One key cause of the high complexity is the connection between the convolution layers and the fully connected layers, which typically requires a high number of parameters. To alleviate this issue, Bag of Features (BoF) pooling has been recently proposed. BoF learns a dictionary, that is used to compile a histogram representation of the input. In this paper, we propose an approach that builds on top of BoF pooling to boost its efficiency by ensuring that the items of the learned dictionary are non-redundant. We propose an additional loss term, based on the pair-wise correlation of the items of the dictionary, which complements the standard loss to explicitly regularize the model to learn a more diverse and rich dictionary. The proposed strategy yields an efficient variant of BoF and further boosts its performance, without any additional parameters.

Non-Linear Spectral Dimensionality Reduction Under Uncertainty

In this paper, we consider the problem of non-linear dimensionality reduction under uncertainty, both from a theoretical and algorithmic perspectives. Since real-world data usually contain measurements with uncertainties and artifacts, the input space in the proposed framework consists of probability distributions to model the uncertainties associated with each sample. We propose a new dimensionality reduction framework, called NGEU, which leverages uncertainty information and directly extends several traditional approaches, e.g., KPCA, MDA/KMFA, to receive as inputs the probability distributions instead of the original data. We show that the proposed NGEU formulation exhibits a global closed-form solution, and we analyze, based on the Rademacher complexity, how the underlying uncertainties theoretically affect the generalization ability of the framework. Empirical results on different datasets show the effectiveness of the proposed framework.

Reducing Redundancy in the Bottleneck Representation of the Autoencoders

Autoencoders are a type of unsupervised neural networks, which can be used to solve various tasks, e.g., dimensionality reduction, image compression, and image denoising. An AE has two goals: (i) compress the original input to a low-dimensional space at the bottleneck of the network topology using an encoder, (ii) reconstruct the input from the representation at the bottleneck using a decoder. Both encoder and decoder are optimized jointly by minimizing a distortion-based loss which implicitly forces the model to keep only those variations of input data that are required to reconstruct the and to reduce redundancies. In this paper, we propose a scheme to explicitly penalize feature redundancies in the bottleneck representation. To this end, we propose an additional loss term, based on the pair-wise correlation of the neurons, which complements the standard reconstruction loss forcing the encoder to learn a more diverse and richer representation of the input. We tested our approach across different tasks: dimensionality reduction using three different dataset, image compression using the MNIST dataset, and image denoising using fashion MNIST. The experimental results show that the proposed loss leads consistently to superior performance compared to the standard AE loss.

Learning to ignore: rethinking attention in CNNs

Recently, there has been an increasing interest in applying attention mechanisms in Convolutional Neural Networks (CNNs) to solve computer vision tasks. Most of these methods learn to explicitly identify and highlight relevant parts of the scene and pass the attended image to further layers of the network. In this paper, we argue that such an approach might not be optimal. Arguably, explicitly learning which parts of the image are relevant is typically harder than learning which parts of the image are less relevant and, thus, should be ignored. In fact, in vision domain, there are many easy-to-identify patterns of irrelevant features. For example, image regions close to the borders are less likely to contain useful information for a classification task. Based on this idea, we propose to reformulate the attention mechanism in CNNs to learn to ignore instead of learning to attend. Specifically, we propose to explicitly learn irrelevant information in the scene and suppress it in the produced representation, keeping only important attributes. This implicit attention scheme can be incorporated into any existing attention mechanism. In this work, we validate this idea using two recent attention methods Squeeze and Excitation (SE) block and Convolutional Block Attention Module (CBAM). Experimental results on different datasets and model architectures show that learning to ignore, i.e., implicit attention, yields superior performance compared to the standard approaches.