Dependence Induced Representations

We study the problem of learning feature representations from a pair of random variables, where we focus on the representations that are induced by their dependence. We provide sufficient and necessary conditions for such dependence induced representations, and illustrate their connections to Hirschfeld--Gebelein--R\'{e}nyi (HGR) maximal correlation functions and minimal sufficient statistics. We characterize a large family of loss functions that can learn dependence induced representations, including cross entropy, hinge loss, and their regularized variants. In particular, we show that the features learned from this family can be expressed as the composition of a loss-dependent function and the maximal correlation function, which reveals a key connection between representations learned from different losses. Our development also gives a statistical interpretation of the neural collapse phenomenon observed in deep classifiers. Finally, we present the learning design based on the feature separation, which allows hyperparameter tuning during inference.

Jet Expansions of Residual Computation

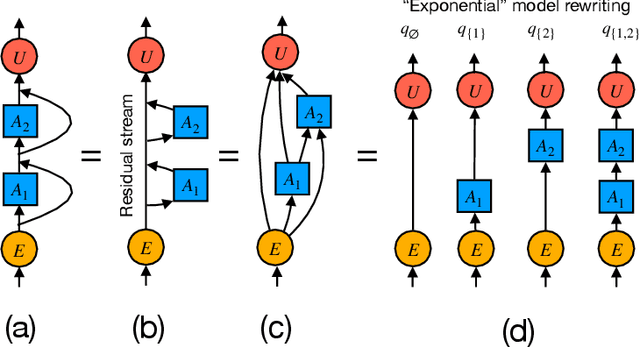
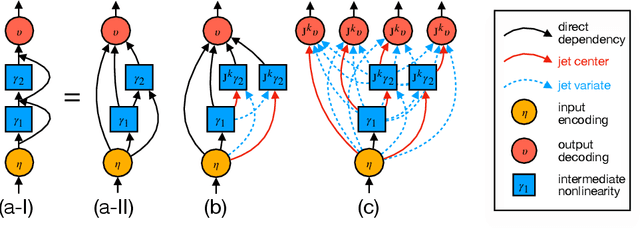
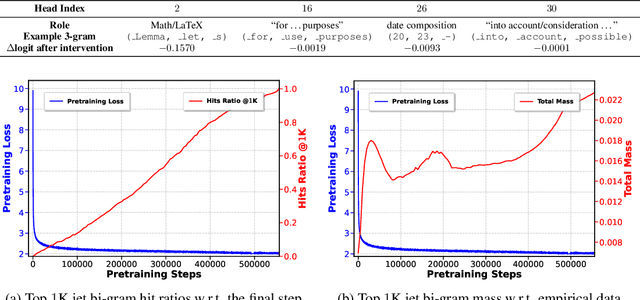
We introduce a framework for expanding residual computational graphs using jets, operators that generalize truncated Taylor series. Our method provides a systematic approach to disentangle contributions of different computational paths to model predictions. In contrast to existing techniques such as distillation, probing, or early decoding, our expansions rely solely on the model itself and requires no data, training, or sampling from the model. We demonstrate how our framework grounds and subsumes logit lens, reveals a (super-)exponential path structure in the recursive residual depth and opens up several applications. These include sketching a transformer large language model with $n$-gram statistics extracted from its computations, and indexing the models' levels of toxicity knowledge. Our approach enables data-free analysis of residual computation for model interpretability, development, and evaluation.

Operator SVD with Neural Networks via Nested Low-Rank Approximation

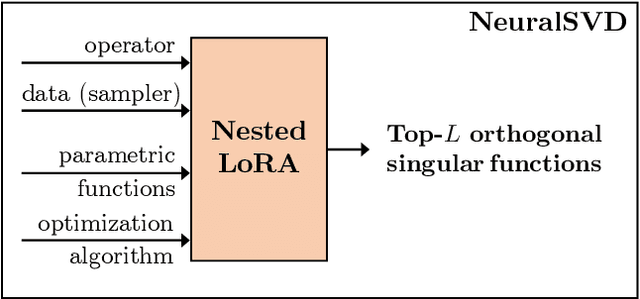
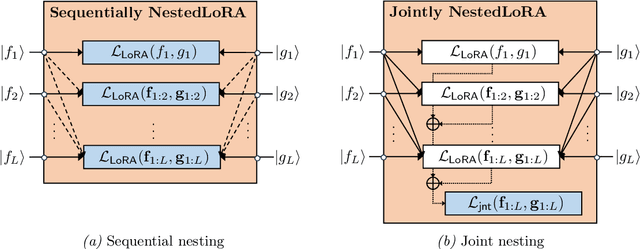
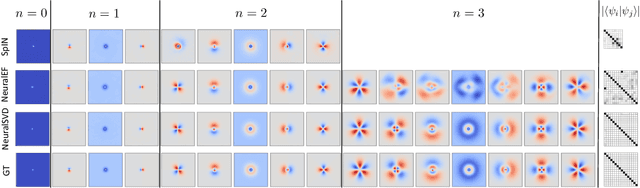
Computing eigenvalue decomposition (EVD) of a given linear operator, or finding its leading eigenvalues and eigenfunctions, is a fundamental task in many machine learning and scientific computing problems. For high-dimensional eigenvalue problems, training neural networks to parameterize the eigenfunctions is considered as a promising alternative to the classical numerical linear algebra techniques. This paper proposes a new optimization framework based on the low-rank approximation characterization of a truncated singular value decomposition, accompanied by new techniques called nesting for learning the top-$L$ singular values and singular functions in the correct order. The proposed method promotes the desired orthogonality in the learned functions implicitly and efficiently via an unconstrained optimization formulation, which is easy to solve with off-the-shelf gradient-based optimization algorithms. We demonstrate the effectiveness of the proposed optimization framework for use cases in computational physics and machine learning.

A Geometric Framework for Neural Feature Learning

We present a novel framework for learning system design based on neural feature extractors by exploiting geometric structures in feature spaces. First, we introduce the feature geometry, which unifies statistical dependence and features in the same functional space with geometric structures. By applying the feature geometry, we formulate each learning problem as solving the optimal feature approximation of the dependence component specified by the learning setting. We propose a nesting technique for designing learning algorithms to learn the optimal features from data samples, which can be applied to off-the-shelf network architectures and optimizers. To demonstrate the application of the nesting technique, we further discuss multivariate learning problems, including conditioned inference and multimodal learning, where we present the optimal features and reveal their connections to classical approaches.

Kernel Subspace and Feature Extraction

We study kernel methods in machine learning from the perspective of feature subspace. We establish a one-to-one correspondence between feature subspaces and kernels and propose an information-theoretic measure for kernels. In particular, we construct a kernel from Hirschfeld--Gebelein--R\'{e}nyi maximal correlation functions, coined the maximal correlation kernel, and demonstrate its information-theoretic optimality. We use the support vector machine (SVM) as an example to illustrate a connection between kernel methods and feature extraction approaches. We show that the kernel SVM on maximal correlation kernel achieves minimum prediction error. Finally, we interpret the Fisher kernel as a special maximal correlation kernel and establish its optimality.

On Distributed Learning with Constant Communication Bits

In this paper, we study a distributed learning problem constrained by constant communication bits. Specifically, we consider the distributed hypothesis testing (DHT) problem where two distributed nodes are constrained to transmit a constant number of bits to a central decoder. In such cases, we show that in order to achieve the optimal error exponents, it suffices to consider the empirical distributions of observed data sequences and encode them to the transmission bits. With such a coding strategy, we develop a geometric approach in the distribution spaces and characterize the optimal schemes. In particular, we show the optimal achievable error exponents and coding schemes for the following cases: (i) both nodes can transmit $\log_23$ bits; (ii) one of the nodes can transmit $1$ bit, and the other node is not constrained; (iii) the joint distribution of the nodes are conditionally independent given one hypothesis. Furthermore, we provide several numerical examples for illustrating the theoretical results. Our results provide theoretical guidance for designing practical distributed learning rules, and the developed approach also reveals new potentials for establishing error exponents for DHT with more general communication constraints.

Maximum Likelihood Estimation for Multimodal Learning with Missing Modality

Multimodal learning has achieved great successes in many scenarios. Compared with unimodal learning, it can effectively combine the information from different modalities to improve the performance of learning tasks. In reality, the multimodal data may have missing modalities due to various reasons, such as sensor failure and data transmission error. In previous works, the information of the modality-missing data has not been well exploited. To address this problem, we propose an efficient approach based on maximum likelihood estimation to incorporate the knowledge in the modality-missing data. Specifically, we design a likelihood function to characterize the conditional distribution of the modality-complete data and the modality-missing data, which is theoretically optimal. Moreover, we develop a generalized form of the softmax function to effectively implement maximum likelihood estimation in an end-to-end manner. Such training strategy guarantees the computability of our algorithm capably. Finally, we conduct a series of experiments on real-world multimodal datasets. Our results demonstrate the effectiveness of the proposed approach, even when 95% of the training data has missing modality.

An Information-theoretic Approach to Unsupervised Feature Selection for High-Dimensional Data

In this paper, we propose an information-theoretic approach to design the functional representations to extract the hidden common structure shared by a set of random variables. The main idea is to measure the common information between the random variables by Watanabe's total correlation, and then find the hidden attributes of these random variables such that the common information is reduced the most given these attributes. We show that these attributes can be characterized by an exponential family specified by the eigen-decomposition of some pairwise joint distribution matrix. Then, we adopt the log-likelihood functions for estimating these attributes as the desired functional representations of the random variables, and show that such representations are informative to describe the common structure. Moreover, we design both the multivariate alternating conditional expectation (MACE) algorithm to compute the proposed functional representations for discrete data, and a novel neural network training approach for continuous or high-dimensional data. Furthermore, we show that our approach has deep connections to existing techniques, such as Hirschfeld-Gebelein-R\'{e}nyi (HGR) maximal correlation, linear principal component analysis (PCA), and consistent functional map, which establishes insightful connections between information theory and machine learning. Finally, the performances of our algorithms are validated by numerical simulations.

An Information Theoretic Interpretation to Deep Neural Networks

It is commonly believed that the hidden layers of deep neural networks (DNNs) attempt to extract informative features for learning tasks. In this paper, we formalize this intuition by showing that the features extracted by DNN coincide with the result of an optimization problem, which we call the `universal feature selection' problem, in a local analysis regime. We interpret the weights training in DNN as the projection of feature functions between feature spaces, specified by the network structure. Our formulation has direct operational meaning in terms of the performance for inference tasks, and gives interpretations to the internal computation results of DNNs. Results of numerical experiments are provided to support the analysis.

An Efficient Approach to Informative Feature Extraction from Multimodal Data

One primary focus in multimodal feature extraction is to find the representations of individual modalities that are maximally correlated. As a well-known measure of dependence, the Hirschfeld-Gebelein-R\'{e}nyi (HGR) maximal correlation becomes an appealing objective because of its operational meaning and desirable properties. However, the strict whitening constraints formalized in the HGR maximal correlation limit its application. To address this problem, this paper proposes Soft-HGR, a novel framework to extract informative features from multiple data modalities. Specifically, our framework prevents the "hard" whitening constraints, while simultaneously preserving the same feature geometry as in the HGR maximal correlation. The objective of Soft-HGR is straightforward, only involving two inner products, which guarantees the efficiency and stability in optimization. We further generalize the framework to handle more than two modalities and missing modalities. When labels are partially available, we enhance the discriminative power of the feature representations by making a semi-supervised adaptation. Empirical evaluation implies that our approach learns more informative feature mappings and is more efficient to optimize.