Jet Expansions of Residual Computation
Paper and Code
Oct 08, 2024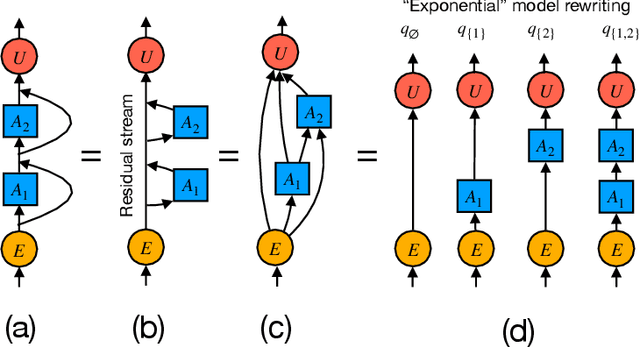

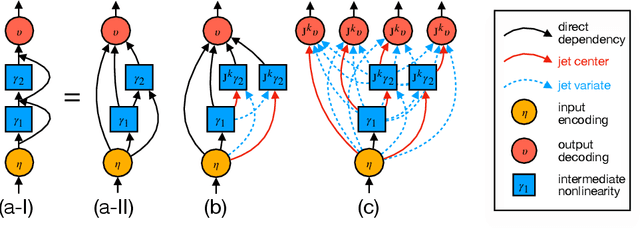
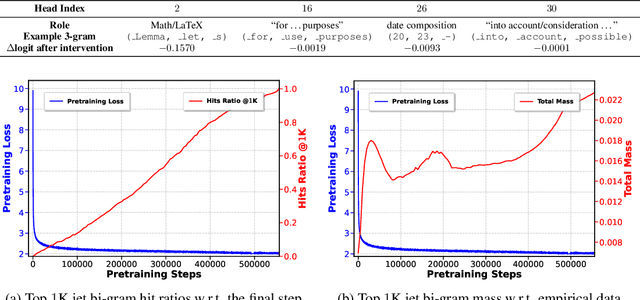
We introduce a framework for expanding residual computational graphs using jets, operators that generalize truncated Taylor series. Our method provides a systematic approach to disentangle contributions of different computational paths to model predictions. In contrast to existing techniques such as distillation, probing, or early decoding, our expansions rely solely on the model itself and requires no data, training, or sampling from the model. We demonstrate how our framework grounds and subsumes logit lens, reveals a (super-)exponential path structure in the recursive residual depth and opens up several applications. These include sketching a transformer large language model with $n$-gram statistics extracted from its computations, and indexing the models' levels of toxicity knowledge. Our approach enables data-free analysis of residual computation for model interpretability, development, and evaluation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge