CoRet: Improved Retriever for Code Editing

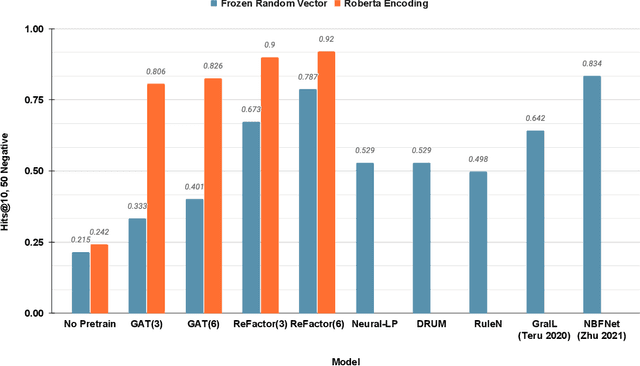
In this paper, we introduce CoRet, a dense retrieval model designed for code-editing tasks that integrates code semantics, repository structure, and call graph dependencies. The model focuses on retrieving relevant portions of a code repository based on natural language queries such as requests to implement new features or fix bugs. These retrieved code chunks can then be presented to a user or to a second code-editing model or agent. To train CoRet, we propose a loss function explicitly designed for repository-level retrieval. On SWE-bench and Long Code Arena's bug localisation datasets, we show that our model substantially improves retrieval recall by at least 15 percentage points over existing models, and ablate the design choices to show their importance in achieving these results.

Hyperparameter Optimization in Machine Learning

Hyperparameters are configuration variables controlling the behavior of machine learning algorithms. They are ubiquitous in machine learning and artificial intelligence and the choice of their values determine the effectiveness of systems based on these technologies. Manual hyperparameter search is often unsatisfactory and becomes unfeasible when the number of hyperparameters is large. Automating the search is an important step towards automating machine learning, freeing researchers and practitioners alike from the burden of finding a good set of hyperparameters by trial and error. In this survey, we present a unified treatment of hyperparameter optimization, providing the reader with examples and insights into the state-of-the-art. We cover the main families of techniques to automate hyperparameter search, often referred to as hyperparameter optimization or tuning, including random and quasi-random search, bandit-, model- and gradient- based approaches. We further discuss extensions, including online, constrained, and multi-objective formulations, touch upon connections with other fields such as meta-learning and neural architecture search, and conclude with open questions and future research directions.

Jet Expansions of Residual Computation

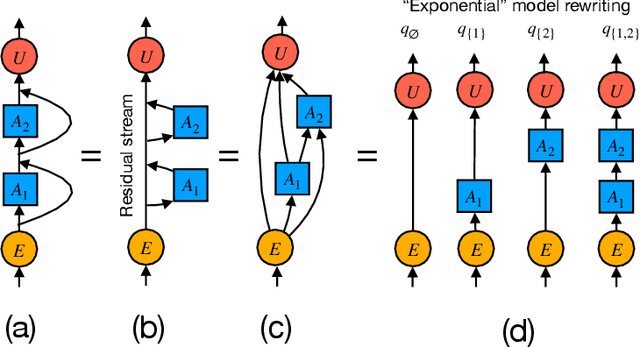
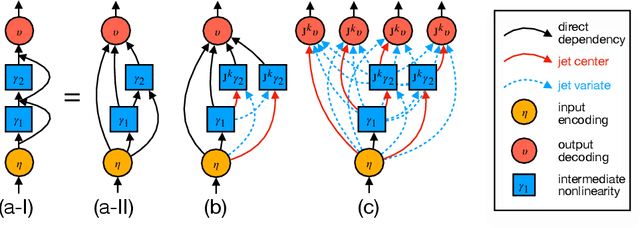
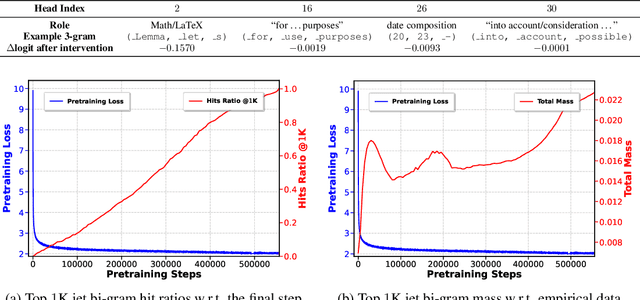
We introduce a framework for expanding residual computational graphs using jets, operators that generalize truncated Taylor series. Our method provides a systematic approach to disentangle contributions of different computational paths to model predictions. In contrast to existing techniques such as distillation, probing, or early decoding, our expansions rely solely on the model itself and requires no data, training, or sampling from the model. We demonstrate how our framework grounds and subsumes logit lens, reveals a (super-)exponential path structure in the recursive residual depth and opens up several applications. These include sketching a transformer large language model with $n$-gram statistics extracted from its computations, and indexing the models' levels of toxicity knowledge. Our approach enables data-free analysis of residual computation for model interpretability, development, and evaluation.

Evaluating Large Language Models with fmeval

fmeval is an open source library to evaluate large language models (LLMs) in a range of tasks. It helps practitioners evaluate their model for task performance and along multiple responsible AI dimensions. This paper presents the library and exposes its underlying design principles: simplicity, coverage, extensibility and performance. We then present how these were implemented in the scientific and engineering choices taken when developing fmeval. A case study demonstrates a typical use case for the library: picking a suitable model for a question answering task. We close by discussing limitations and further work in the development of the library. fmeval can be found at https://github.com/aws/fmeval.

Explaining Probabilistic Models with Distributional Values

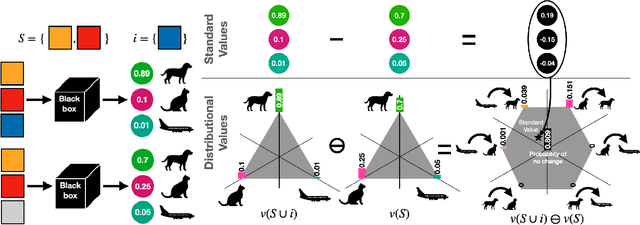
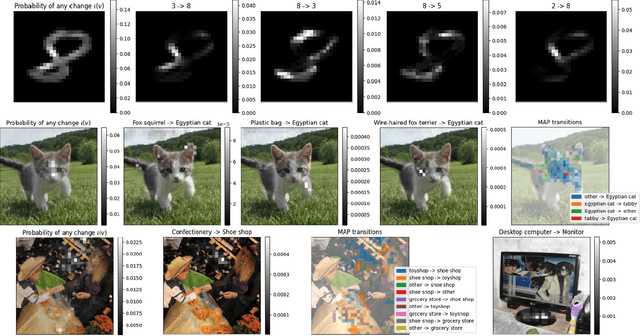
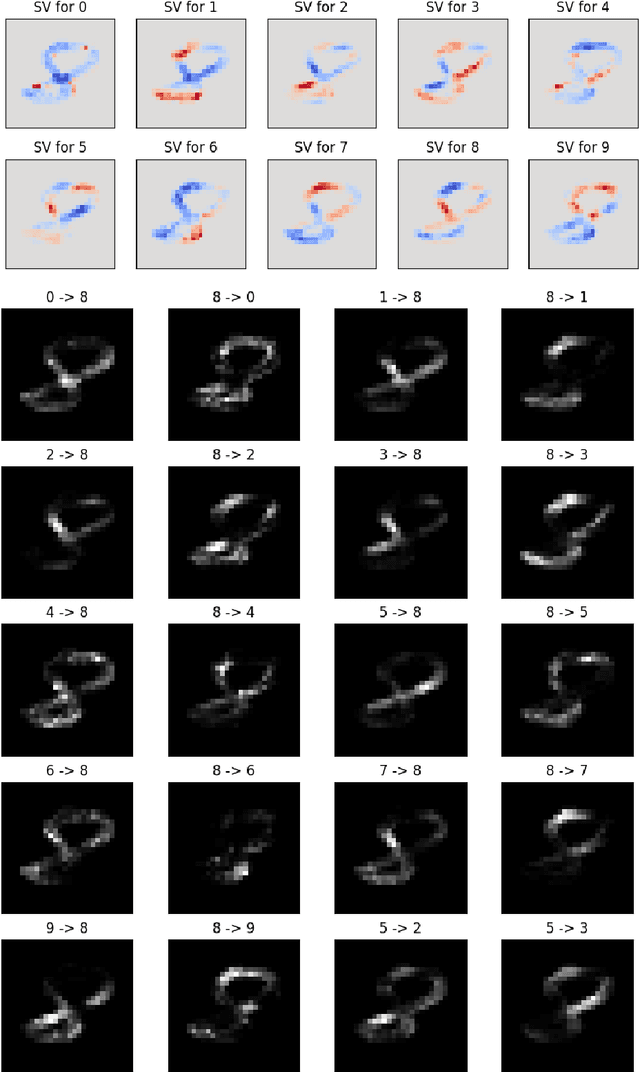
A large branch of explainable machine learning is grounded in cooperative game theory. However, research indicates that game-theoretic explanations may mislead or be hard to interpret. We argue that often there is a critical mismatch between what one wishes to explain (e.g. the output of a classifier) and what current methods such as SHAP explain (e.g. the scalar probability of a class). This paper addresses such gap for probabilistic models by generalising cooperative games and value operators. We introduce the distributional values, random variables that track changes in the model output (e.g. flipping of the predicted class) and derive their analytic expressions for games with Gaussian, Bernoulli and Categorical payoffs. We further establish several characterising properties, and show that our framework provides fine-grained and insightful explanations with case studies on vision and language models.

DAG Learning on the Permutahedron

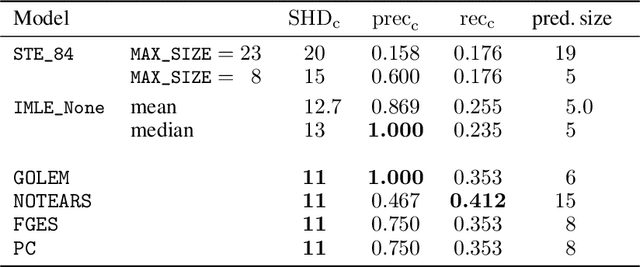
We propose a continuous optimization framework for discovering a latent directed acyclic graph (DAG) from observational data. Our approach optimizes over the polytope of permutation vectors, the so-called Permutahedron, to learn a topological ordering. Edges can be optimized jointly, or learned conditional on the ordering via a non-differentiable subroutine. Compared to existing continuous optimization approaches our formulation has a number of advantages including: 1. validity: optimizes over exact DAGs as opposed to other relaxations optimizing approximate DAGs; 2. modularity: accommodates any edge-optimization procedure, edge structural parameterization, and optimization loss; 3. end-to-end: either alternately iterates between node-ordering and edge-optimization, or optimizes them jointly. We demonstrate, on real-world data problems in protein-signaling and transcriptional network discovery, that our approach lies on the Pareto frontier of two key metrics, the SID and SHD.

Learning Discrete Directed Acyclic Graphs via Backpropagation

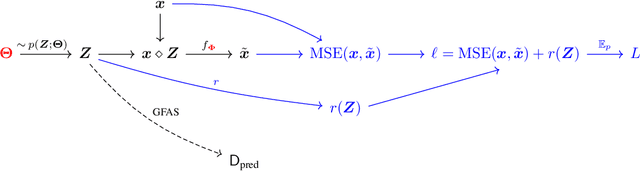
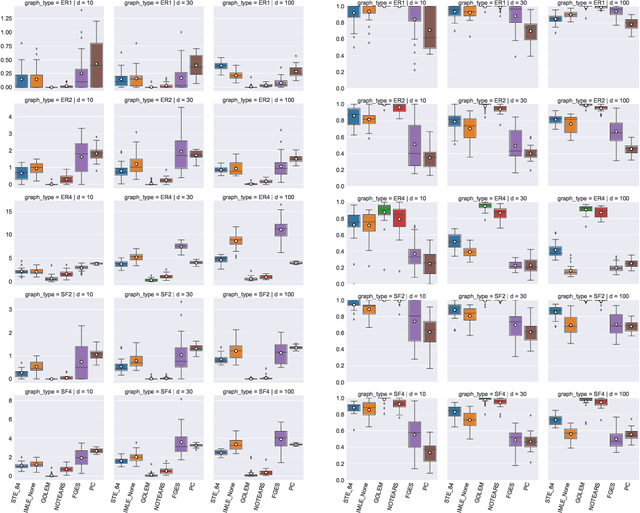
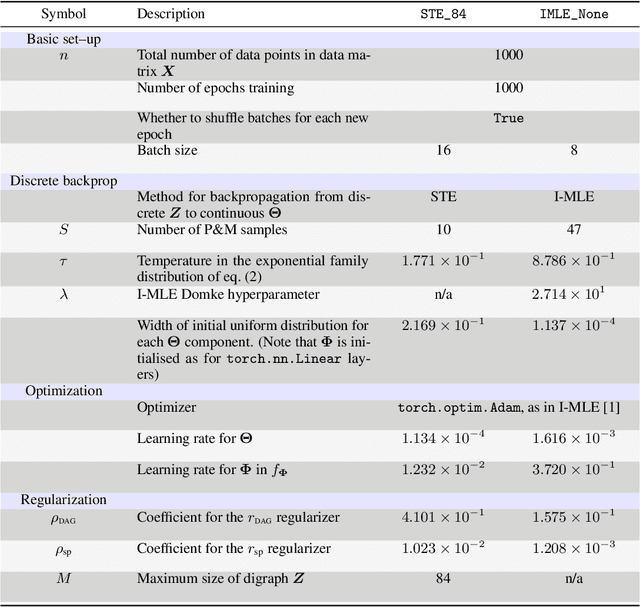
Recently continuous relaxations have been proposed in order to learn Directed Acyclic Graphs (DAGs) from data by backpropagation, instead of using combinatorial optimization. However, a number of techniques for fully discrete backpropagation could instead be applied. In this paper, we explore that direction and propose DAG-DB, a framework for learning DAGs by Discrete Backpropagation. Based on the architecture of Implicit Maximum Likelihood Estimation [I-MLE, arXiv:2106.01798], DAG-DB adopts a probabilistic approach to the problem, sampling binary adjacency matrices from an implicit probability distribution. DAG-DB learns a parameter for the distribution from the loss incurred by each sample, performing competitively using either of two fully discrete backpropagation techniques, namely I-MLE and Straight-Through Estimation.

Adaptive Perturbation-Based Gradient Estimation for Discrete Latent Variable Models

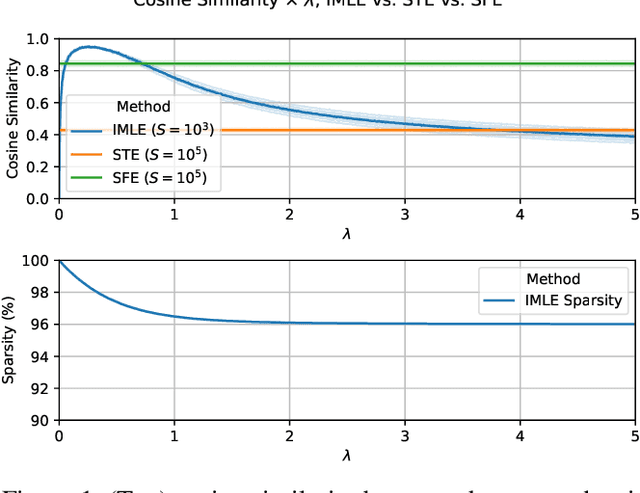
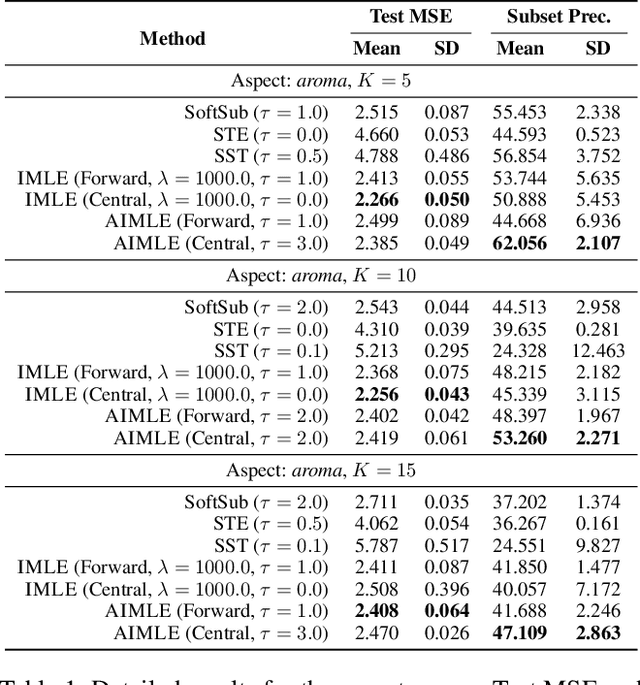
The integration of discrete algorithmic components in deep learning architectures has numerous applications. Recently, Implicit Maximum Likelihood Estimation (IMLE, Niepert, Minervini, and Franceschi 2021), a class of gradient estimators for discrete exponential family distributions, was proposed by combining implicit differentiation through perturbation with the path-wise gradient estimator. However, due to the finite difference approximation of the gradients, it is especially sensitive to the choice of the finite difference step size which needs to be specified by the user. In this work, we present Adaptive IMLE (AIMLE) the first adaptive gradient estimator for complex discrete distributions: it adaptively identifies the target distribution for IMLE by trading off the density of gradient information with the degree of bias in the gradient estimates. We empirically evaluate our estimator on synthetic examples, as well as on Learning to Explain, Discrete Variational Auto-Encoders, and Neural Relational Inference tasks. In our experiments, we show that our adaptive gradient estimator can produce faithful estimates while requiring orders of magnitude fewer samples than other gradient estimators.

ReFactorGNNs: Revisiting Factorisation-based Models from a Message-Passing Perspective

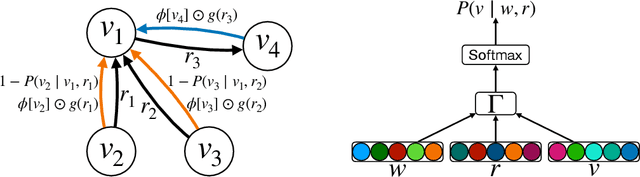
Factorisation-based Models (FMs), such as DistMult, have enjoyed enduring success for Knowledge Graph Completion (KGC) tasks, often outperforming Graph Neural Networks (GNNs). However, unlike GNNs, FMs struggle to incorporate node features and to generalise to unseen nodes in inductive settings. Our work bridges the gap between FMs and GNNs by proposing ReFactorGNNs. This new architecture draws upon both modelling paradigms, which previously were largely thought of as disjoint. Concretely, using a message-passing formalism, we show how FMs can be cast as GNNs by reformulating the gradient descent procedure as message-passing operations, which forms the basis of our ReFactorGNNs. Across a multitude of well-established KGC benchmarks, our ReFactorGNNs achieve comparable transductive performance to FMs, and state-of-the-art inductive performance while using an order of magnitude fewer parameters.

Implicit MLE: Backpropagating Through Discrete Exponential Family Distributions

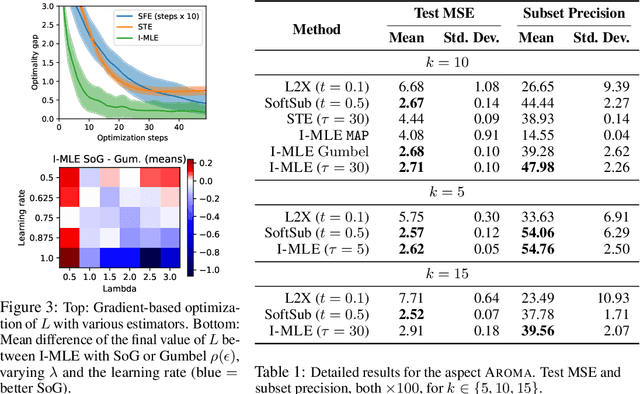
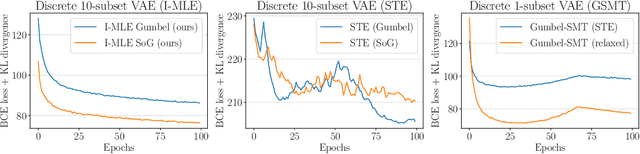
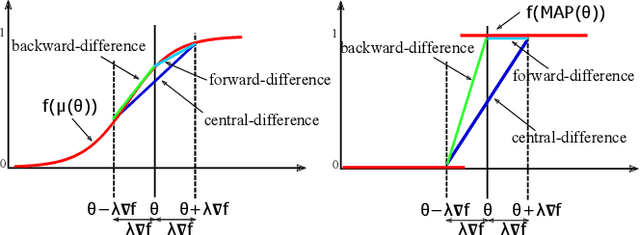
Integrating discrete probability distributions and combinatorial optimization problems into neural networks has numerous applications but poses several challenges. We propose Implicit Maximum Likelihood Estimation (I-MLE), a framework for end-to-end learning of models combining discrete exponential family distributions and differentiable neural components. I-MLE is widely applicable: it only requires the ability to compute the most probable states; and does not rely on smooth relaxations. The framework encompasses several approaches, such as perturbation-based implicit differentiation and recent methods to differentiate through black-box combinatorial solvers. We introduce a novel class of noise distributions for approximating marginals via perturb-and-MAP. Moreover, we show that I-MLE simplifies to maximum likelihood estimation when used in some recently studied learning settings that involve combinatorial solvers. Experiments on several datasets suggest that I-MLE is competitive with and often outperforms existing approaches which rely on problem-specific relaxations.