Andrew J. Wren
Learning Discrete Directed Acyclic Graphs via Backpropagation
Oct 27, 2022
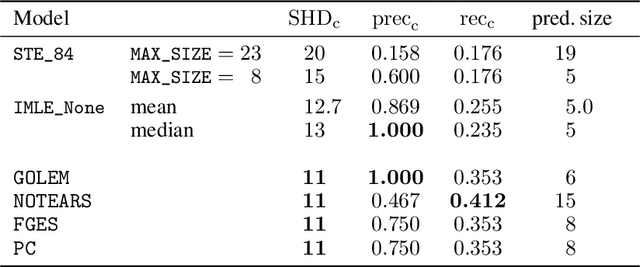
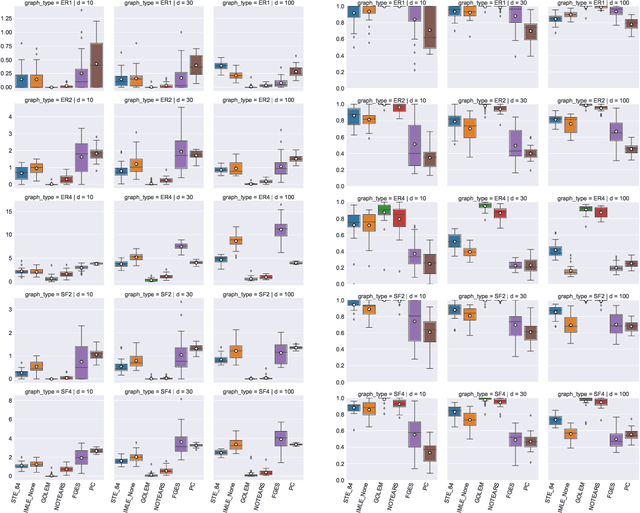
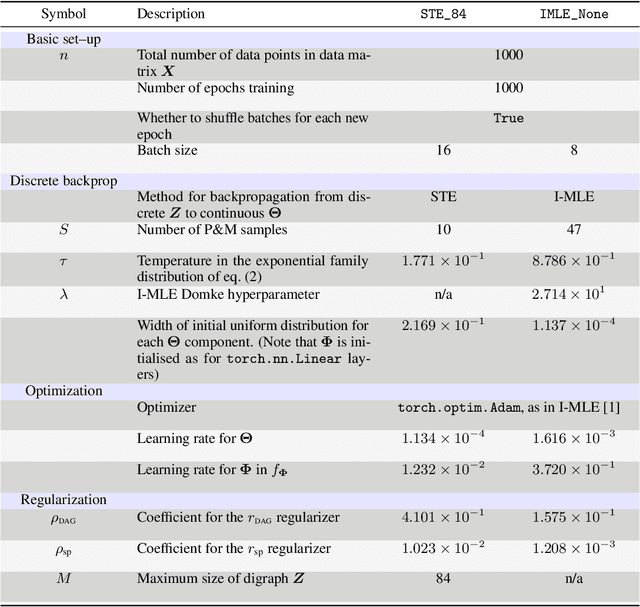
Abstract:Recently continuous relaxations have been proposed in order to learn Directed Acyclic Graphs (DAGs) from data by backpropagation, instead of using combinatorial optimization. However, a number of techniques for fully discrete backpropagation could instead be applied. In this paper, we explore that direction and propose DAG-DB, a framework for learning DAGs by Discrete Backpropagation. Based on the architecture of Implicit Maximum Likelihood Estimation [I-MLE, arXiv:2106.01798], DAG-DB adopts a probabilistic approach to the problem, sampling binary adjacency matrices from an implicit probability distribution. DAG-DB learns a parameter for the distribution from the loss incurred by each sample, performing competitively using either of two fully discrete backpropagation techniques, namely I-MLE and Straight-Through Estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge