ReFactorGNNs: Revisiting Factorisation-based Models from a Message-Passing Perspective

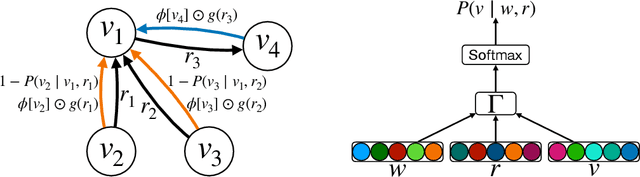
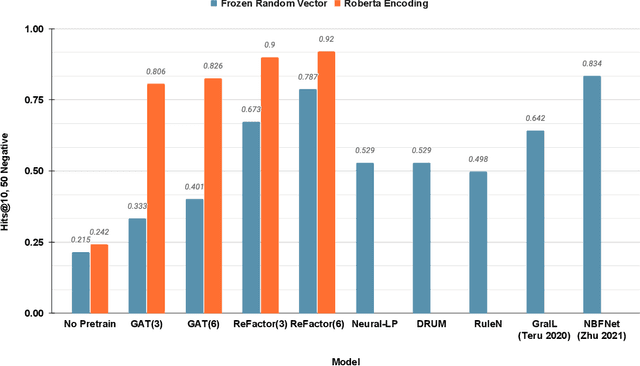
Factorisation-based Models (FMs), such as DistMult, have enjoyed enduring success for Knowledge Graph Completion (KGC) tasks, often outperforming Graph Neural Networks (GNNs). However, unlike GNNs, FMs struggle to incorporate node features and to generalise to unseen nodes in inductive settings. Our work bridges the gap between FMs and GNNs by proposing ReFactorGNNs. This new architecture draws upon both modelling paradigms, which previously were largely thought of as disjoint. Concretely, using a message-passing formalism, we show how FMs can be cast as GNNs by reformulating the gradient descent procedure as message-passing operations, which forms the basis of our ReFactorGNNs. Across a multitude of well-established KGC benchmarks, our ReFactorGNNs achieve comparable transductive performance to FMs, and state-of-the-art inductive performance while using an order of magnitude fewer parameters.