Universally Optimal Watermarking Schemes for LLMs: from Theory to Practice

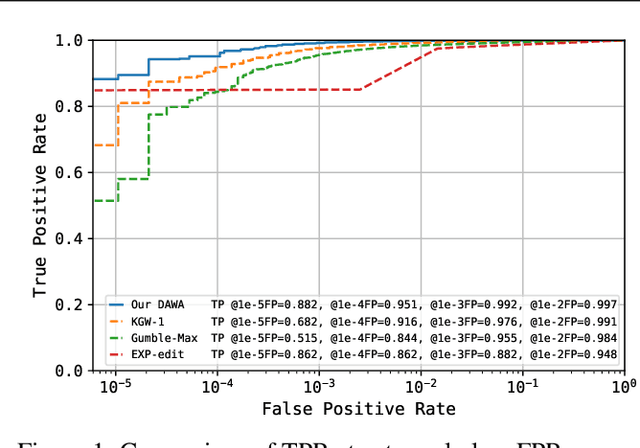
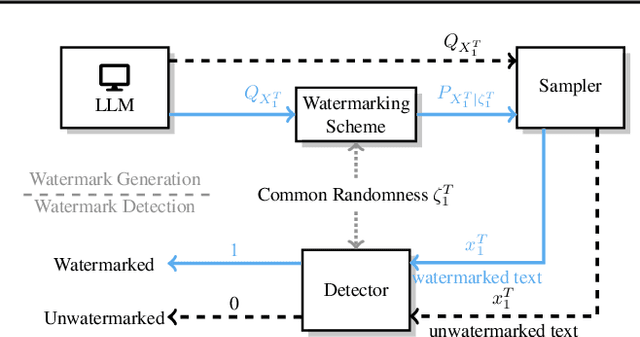
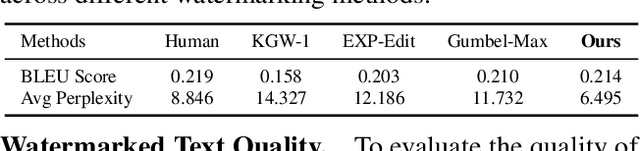
Large Language Models (LLMs) boosts human efficiency but also poses misuse risks, with watermarking serving as a reliable method to differentiate AI-generated content from human-created text. In this work, we propose a novel theoretical framework for watermarking LLMs. Particularly, we jointly optimize both the watermarking scheme and detector to maximize detection performance, while controlling the worst-case Type-I error and distortion in the watermarked text. Within our framework, we characterize the universally minimum Type-II error, showing a fundamental trade-off between detection performance and distortion. More importantly, we identify the optimal type of detectors and watermarking schemes. Building upon our theoretical analysis, we introduce a practical, model-agnostic and computationally efficient token-level watermarking algorithm that invokes a surrogate model and the Gumbel-max trick. Empirical results on Llama-13B and Mistral-8$\times$7B demonstrate the effectiveness of our method. Furthermore, we also explore how robustness can be integrated into our theoretical framework, which provides a foundation for designing future watermarking systems with improved resilience to adversarial attacks.

Information-Theoretic Generalization Bounds for Deep Neural Networks

Deep neural networks (DNNs) exhibit an exceptional capacity for generalization in practical applications. This work aims to capture the effect and benefits of depth for supervised learning via information-theoretic generalization bounds. We first derive two hierarchical bounds on the generalization error in terms of the Kullback-Leibler (KL) divergence or the 1-Wasserstein distance between the train and test distributions of the network internal representations. The KL divergence bound shrinks as the layer index increases, while the Wasserstein bound implies the existence of a layer that serves as a generalization funnel, which attains a minimal 1-Wasserstein distance. Analytic expressions for both bounds are derived under the setting of binary Gaussian classification with linear DNNs. To quantify the contraction of the relevant information measures when moving deeper into the network, we analyze the strong data processing inequality (SDPI) coefficient between consecutive layers of three regularized DNN models: Dropout, DropConnect, and Gaussian noise injection. This enables refining our generalization bounds to capture the contraction as a function of the network architecture parameters. Specializing our results to DNNs with a finite parameter space and the Gibbs algorithm reveals that deeper yet narrower network architectures generalize better in those examples, although how broadly this statement applies remains a question.

How Does Pseudo-Labeling Affect the Generalization Error of the Semi-Supervised Gibbs Algorithm?

This paper provides an exact characterization of the expected generalization error (gen-error) for semi-supervised learning (SSL) with pseudo-labeling via the Gibbs algorithm. This characterization is expressed in terms of the symmetrized KL information between the output hypothesis, the pseudo-labeled dataset, and the labeled dataset. It can be applied to obtain distribution-free upper and lower bounds on the gen-error. Our findings offer new insights that the generalization performance of SSL with pseudo-labeling is affected not only by the information between the output hypothesis and input training data but also by the information {\em shared} between the {\em labeled} and {\em pseudo-labeled} data samples. To deepen our understanding, we further explore two examples -- mean estimation and logistic regression. In particular, we analyze how the ratio of the number of unlabeled to labeled data $\lambda$ affects the gen-error under both scenarios. As $\lambda$ increases, the gen-error for mean estimation decreases and then saturates at a value larger than when all the samples are labeled, and the gap can be quantified {\em exactly} with our analysis, and is dependent on the \emph{cross-covariance} between the labeled and pseudo-labeled data sample. In logistic regression, the gen-error and the variance component of the excess risk also decrease as $\lambda$ increases.

Information-Theoretic Generalization Bounds for Iterative Semi-Supervised Learning

We consider iterative semi-supervised learning (SSL) algorithms that iteratively generate pseudo-labels for a large amount unlabelled data to progressively refine the model parameters. In particular, we seek to understand the behaviour of the {\em generalization error} of iterative SSL algorithms using information-theoretic principles. To obtain bounds that are amenable to numerical evaluation, we first work with a simple model -- namely, the binary Gaussian mixture model. Our theoretical results suggest that when the class conditional variances are not too large, the upper bound on the generalization error decreases monotonically with the number of iterations, but quickly saturates. The theoretical results on the simple model are corroborated by extensive experiments on several benchmark datasets such as the MNIST and CIFAR datasets in which we notice that the generalization error improves after several pseudo-labelling iterations, but saturates afterwards.

Optimal Resolution of Change-Point Detection with Empirically Observed Statistics and Erasures

This paper revisits the offline change-point detection problem from a statistical learning perspective. Instead of assuming that the underlying pre- and post-change distributions are known, it is assumed that we have partial knowledge of these distributions based on empirically observed statistics in the form of training sequences. Our problem formulation finds a variety of real-life applications from detecting when climate change occurred to detecting when a virus mutated. Using the training sequences as well as the test sequence consisting of a single-change and allowing for the erasure or rejection option, we derive the optimal resolution between the estimated and true change-points under two different asymptotic regimes on the undetected error probability---namely, the large and moderate deviations regimes. In both regimes, strong converses are also proved. In the moderate deviations case, the optimal resolution is a simple function of a symmetrized version of the chi-square distance.