CiQi-Agent: Aligning Vision, Tools and Aesthetics in Multimodal Agent for Cultural Reasoning on Chinese Porcelains

The connoisseurship of antique Chinese porcelain demands extensive historical expertise, material understanding, and aesthetic sensitivity, making it difficult for non-specialists to engage. To democratize cultural-heritage understanding and assist expert connoisseurship, we introduce CiQi-Agent -- a domain-specific Porcelain Connoisseurship Agent for intelligent analysis of antique Chinese porcelain. CiQi-Agent supports multi-image porcelain inputs and enables vision tool invocation and multimodal retrieval-augmented generation, performing fine-grained connoisseurship analysis across six attributes: dynasty, reign period, kiln site, glaze color, decorative motif, and vessel shape. Beyond attribute classification, it captures subtle visual details, retrieves relevant domain knowledge, and integrates visual and textual evidence to produce coherent, explainable connoisseurship descriptions. To achieve this capability, we construct a large-scale, expert-annotated dataset CiQi-VQA, comprising 29,596 porcelain specimens, 51,553 images, and 557,940 visual question--answering pairs, and further establish a comprehensive benchmark CiQi-Bench aligned with the previously mentioned six attributes. CiQi-Agent is trained through supervised fine-tuning, reinforcement learning, and a tool-augmented reasoning framework that integrates two categories of tools: a vision tool and multimodal retrieval tools. Experimental results show that CiQi-Agent (7B) outperforms all competitive open- and closed-source models across all six attributes on CiQi-Bench, achieving on average 12.2\% higher accuracy than GPT-5. The model and dataset have been released and are publicly available at https://huggingface.co/datasets/SII-Monument-Valley/CiQi-VQA.

Adaptive Theory of Mind for LLM-based Multi-Agent Coordination

Theory of Mind (ToM) refers to the ability to reason about others' mental states, and higher-order ToM involves considering that others also possess their own ToM. Equipping large language model (LLM)-driven agents with ToM has long been considered to improve their coordination in multiagent collaborative tasks. However, we find that misaligned ToM orders-mismatches in the depth of ToM reasoning between agents-can lead to insufficient or excessive reasoning about others, thereby impairing their coordination. To address this issue, we design an adaptive ToM (A-ToM) agent, which can align in ToM orders with its partner. Based on prior interactions, the agent estimates the partner's likely ToM order and leverages this estimation to predict the partner's action, thereby facilitating behavioral coordination. We conduct empirical evaluations on four multi-agent coordination tasks: a repeated matrix game, two grid navigation tasks and an Overcooked task. The results validate our findings on ToM alignment and demonstrate the effectiveness of our A-ToM agent. Furthermore, we discuss the generalizability of our A-ToM to non-LLM-based agents, as well as what would diminish the importance of ToM alignment.

RAPO: Risk-Aware Preference Optimization for Generalizable Safe Reasoning

Large Reasoning Models (LRMs) have achieved tremendous success with their chain-of-thought (CoT) reasoning, yet also face safety issues similar to those of basic language models. In particular, while algorithms are designed to guide them to deliberately refuse harmful prompts with safe reasoning, this process often fails to generalize against diverse and complex jailbreak attacks. In this work, we attribute these failures to the generalization of the safe reasoning process, particularly their insufficiency against complex attack prompts. We provide both theoretical and empirical evidence to show the necessity of a more sufficient safe reasoning process to defend against advanced attack prompts. Building on this insight, we propose a Risk-Aware Preference Optimization (RAPO) framework that enables LRM to adaptively identify and address the safety risks with appropriate granularity in its thinking content. Extensive experiments demonstrate that RAPO successfully generalizes multiple LRMs' safe reasoning adaptively across diverse attack prompts whilst preserving general utility, contributing a robust alignment technique for LRM safety. Our code is available at https://github.com/weizeming/RAPO.

MAGIC: A Co-Evolving Attacker-Defender Adversarial Game for Robust LLM Safety

Ensuring robust safety alignment is crucial for Large Language Models (LLMs), yet existing defenses often lag behind evolving adversarial attacks due to their \textbf{reliance on static, pre-collected data distributions}. In this paper, we introduce \textbf{MAGIC}, a novel multi-turn multi-agent reinforcement learning framework that formulates LLM safety alignment as an adversarial asymmetric game. Specifically, an attacker agent learns to iteratively rewrite original queries into deceptive prompts, while a defender agent simultaneously optimizes its policy to recognize and refuse such inputs. This dynamic process triggers a \textbf{co-evolution}, where the attacker's ever-changing strategies continuously uncover long-tail vulnerabilities, driving the defender to generalize to unseen attack patterns. Remarkably, we observe that the attacker, endowed with initial reasoning ability, evolves \textbf{novel, previously unseen combinatorial strategies} through iterative RL training, underscoring our method's substantial potential. Theoretically, we provide insights into a more robust game equilibrium and derive safety guarantees. Extensive experiments validate our framework's effectiveness, demonstrating superior defense success rates without compromising the helpfulness of the model. Our code is available at https://github.com/BattleWen/MAGIC.

LLMRouterBench: A Massive Benchmark and Unified Framework for LLM Routing

Large language model (LLM) routing assigns each query to the most suitable model from an ensemble. We introduce LLMRouterBench, a large-scale benchmark and unified framework for LLM routing. It comprises over 400K instances from 21 datasets and 33 models. Moreover, it provides comprehensive metrics for both performance-oriented routing and performance-cost trade-off routing, and integrates 10 representative routing baselines. Using LLMRouterBench, we systematically re-evaluate the field. While confirming strong model complementarity-the central premise of LLM routing-we find that many routing methods exhibit similar performance under unified evaluation, and several recent approaches, including commercial routers, fail to reliably outperform a simple baseline. Meanwhile, a substantial gap remains to the Oracle, driven primarily by persistent model-recall failures. We further show that backbone embedding models have limited impact, that larger ensembles exhibit diminishing returns compared to careful model curation, and that the benchmark also enables latency-aware analysis. All code and data are available at https://github.com/ynulihao/LLMRouterBench.

KALE: Enhancing Knowledge Manipulation in Large Language Models via Knowledge-aware Learning

Despite the impressive performance of large language models (LLMs) pretrained on vast knowledge corpora, advancing their knowledge manipulation-the ability to effectively recall, reason, and transfer relevant knowledge-remains challenging. Existing methods mainly leverage Supervised Fine-Tuning (SFT) on labeled datasets to enhance LLMs' knowledge manipulation ability. However, we observe that SFT models still exhibit the known&incorrect phenomenon, where they explicitly possess relevant knowledge for a given question but fail to leverage it for correct answers. To address this challenge, we propose KALE (Knowledge-Aware LEarning)-a post-training framework that leverages knowledge graphs (KGs) to generate high-quality rationales and enhance LLMs' knowledge manipulation ability. Specifically, KALE first introduces a Knowledge-Induced (KI) data synthesis method that efficiently extracts multi-hop reasoning paths from KGs to generate high-quality rationales for question-answer pairs. Then, KALE employs a Knowledge-Aware (KA) fine-tuning paradigm that enhances knowledge manipulation by internalizing rationale-guided reasoning through minimizing the KL divergence between predictions with and without rationales. Extensive experiments on eight popular benchmarks across six different LLMs demonstrate the effectiveness of KALE, achieving accuracy improvements of up to 11.72% and an average of 4.18%.

PerPilot: Personalizing VLM-based Mobile Agents via Memory and Exploration

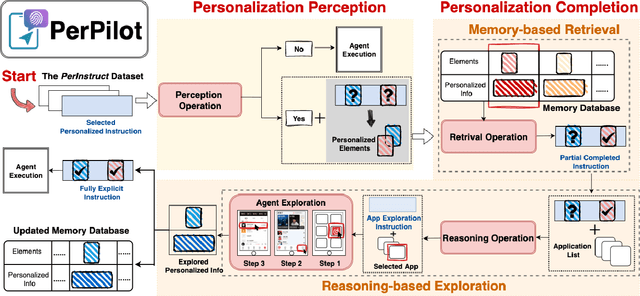
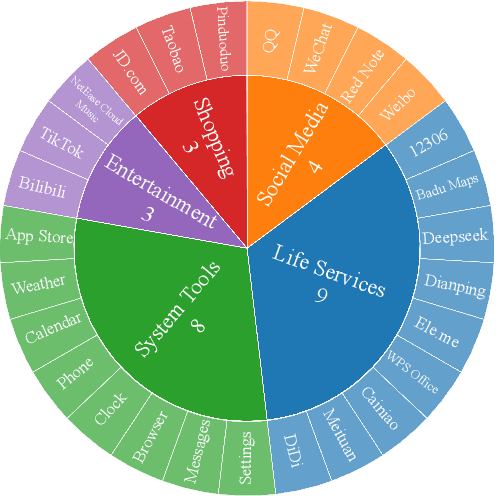
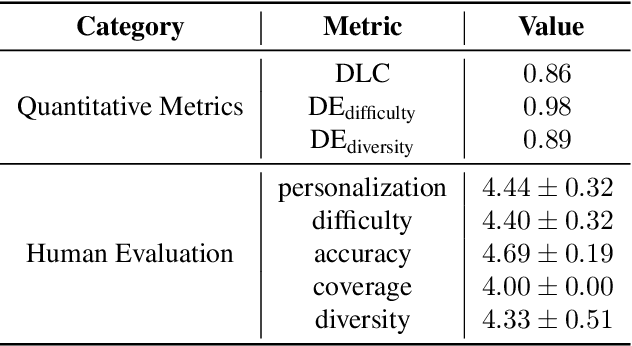
Vision language model (VLM)-based mobile agents show great potential for assisting users in performing instruction-driven tasks. However, these agents typically struggle with personalized instructions -- those containing ambiguous, user-specific context -- a challenge that has been largely overlooked in previous research. In this paper, we define personalized instructions and introduce PerInstruct, a novel human-annotated dataset covering diverse personalized instructions across various mobile scenarios. Furthermore, given the limited personalization capabilities of existing mobile agents, we propose PerPilot, a plug-and-play framework powered by large language models (LLMs) that enables mobile agents to autonomously perceive, understand, and execute personalized user instructions. PerPilot identifies personalized elements and autonomously completes instructions via two complementary approaches: memory-based retrieval and reasoning-based exploration. Experimental results demonstrate that PerPilot effectively handles personalized tasks with minimal user intervention and progressively improves its performance with continued use, underscoring the importance of personalization-aware reasoning for next-generation mobile agents. The dataset and code are available at: https://github.com/xinwang-nwpu/PerPilot

SafeWork-R1: Coevolving Safety and Intelligence under the AI-45$^{\circ}$ Law

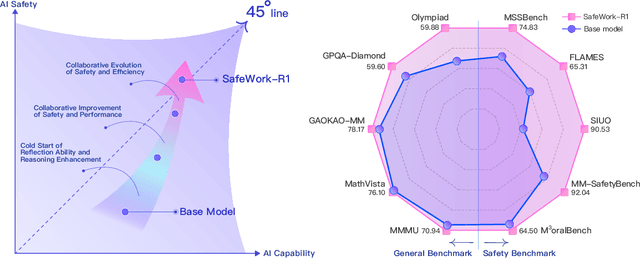
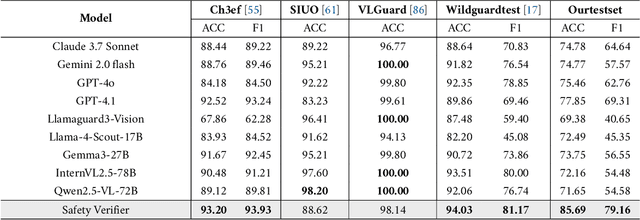
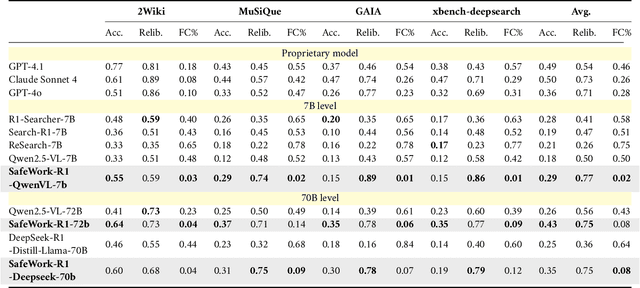
We introduce SafeWork-R1, a cutting-edge multimodal reasoning model that demonstrates the coevolution of capabilities and safety. It is developed by our proposed SafeLadder framework, which incorporates large-scale, progressive, safety-oriented reinforcement learning post-training, supported by a suite of multi-principled verifiers. Unlike previous alignment methods such as RLHF that simply learn human preferences, SafeLadder enables SafeWork-R1 to develop intrinsic safety reasoning and self-reflection abilities, giving rise to safety `aha' moments. Notably, SafeWork-R1 achieves an average improvement of $46.54\%$ over its base model Qwen2.5-VL-72B on safety-related benchmarks without compromising general capabilities, and delivers state-of-the-art safety performance compared to leading proprietary models such as GPT-4.1 and Claude Opus 4. To further bolster its reliability, we implement two distinct inference-time intervention methods and a deliberative search mechanism, enforcing step-level verification. Finally, we further develop SafeWork-R1-InternVL3-78B, SafeWork-R1-DeepSeek-70B, and SafeWork-R1-Qwen2.5VL-7B. All resulting models demonstrate that safety and capability can co-evolve synergistically, highlighting the generalizability of our framework in building robust, reliable, and trustworthy general-purpose AI.

Unsupervised Skill Discovery through Skill Regions Differentiation

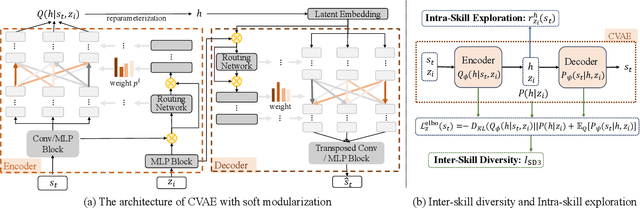
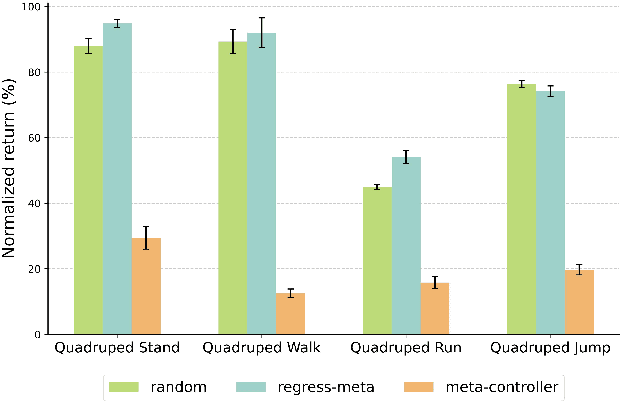
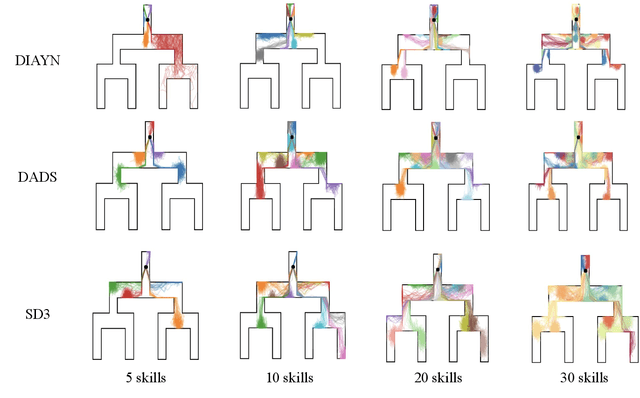
Unsupervised Reinforcement Learning (RL) aims to discover diverse behaviors that can accelerate the learning of downstream tasks. Previous methods typically focus on entropy-based exploration or empowerment-driven skill learning. However, entropy-based exploration struggles in large-scale state spaces (e.g., images), and empowerment-based methods with Mutual Information (MI) estimations have limitations in state exploration. To address these challenges, we propose a novel skill discovery objective that maximizes the deviation of the state density of one skill from the explored regions of other skills, encouraging inter-skill state diversity similar to the initial MI objective. For state-density estimation, we construct a novel conditional autoencoder with soft modularization for different skill policies in high-dimensional space. Meanwhile, to incentivize intra-skill exploration, we formulate an intrinsic reward based on the learned autoencoder that resembles count-based exploration in a compact latent space. Through extensive experiments in challenging state and image-based tasks, we find our method learns meaningful skills and achieves superior performance in various downstream tasks.

The Avengers: A Simple Recipe for Uniting Smaller Language Models to Challenge Proprietary Giants

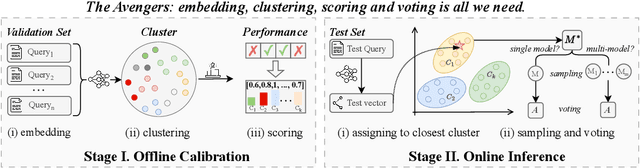
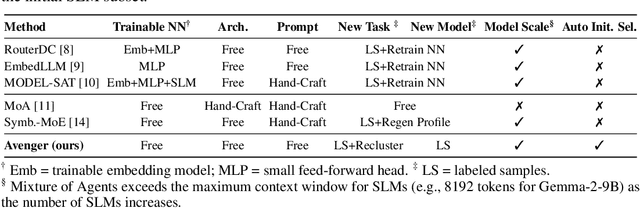
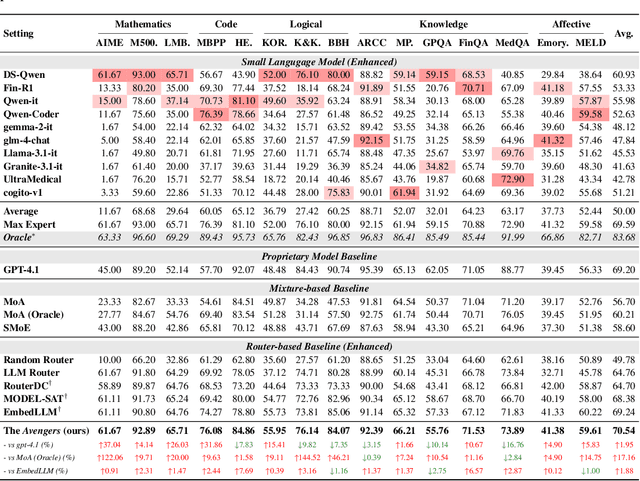
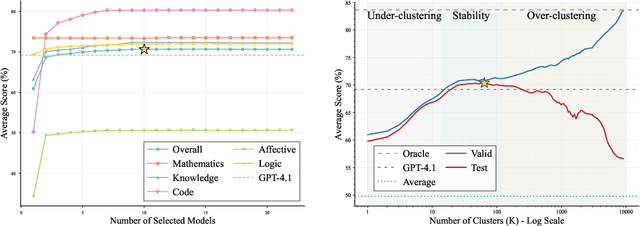
As proprietary giants increasingly dominate the race for ever-larger language models, a pressing question arises for the open-source community: can smaller models remain competitive across a broad range of tasks? In this paper, we present the Avengers--a simple recipe that effectively leverages the collective intelligence of open-source, smaller language models. Our framework is built upon four lightweight operations: (i) embedding: encode queries using a text embedding model; (ii) clustering: group queries based on their semantic similarity; (iii) scoring: scores each model's performance within each cluster; and (iv) voting: improve outputs via repeated sampling and voting. At inference time, each query is embedded and assigned to its nearest cluster. The top-performing model(s) within that cluster are selected to generate the response using the Self-Consistency or its multi-model variant. Remarkably, with 10 open-source models (~7B parameters each), the Avengers collectively outperforms GPT-4.1 on 10 out of 15 datasets (spanning mathematics, code, logic, knowledge, and affective tasks). In particular, it surpasses GPT-4.1 on mathematics tasks by 18.21% and on code tasks by 7.46%. Furthermore, the Avengers delivers superior out-of-distribution generalization, and remains robust across various embedding models, clustering algorithms, ensemble strategies, and values of its sole parameter--the number of clusters. We have open-sourced the code on GitHub: https://github.com/ZhangYiqun018/Avengers