A Unified View on Learning Unnormalized Distributions via Noise-Contrastive Estimation

This paper studies a family of estimators based on noise-contrastive estimation (NCE) for learning unnormalized distributions. The main contribution of this work is to provide a unified perspective on various methods for learning unnormalized distributions, which have been independently proposed and studied in separate research communities, through the lens of NCE. This unified view offers new insights into existing estimators. Specifically, for exponential families, we establish the finite-sample convergence rates of the proposed estimators under a set of regularity assumptions, most of which are new.

Doubly Robust Inference in Causal Latent Factor Models

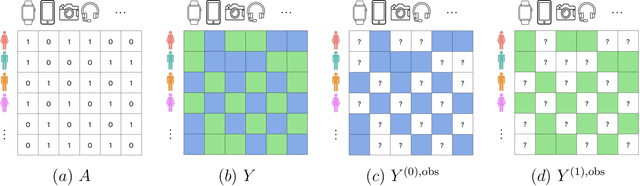
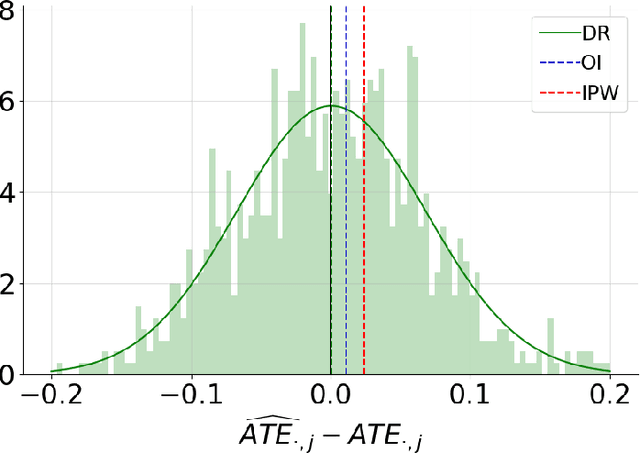
This article introduces a new framework for estimating average treatment effects under unobserved confounding in modern data-rich environments featuring large numbers of units and outcomes. The proposed estimator is doubly robust, combining outcome imputation, inverse probability weighting, and a novel cross-fitting procedure for matrix completion. We derive finite-sample and asymptotic guarantees, and show that the error of the new estimator converges to a mean-zero Gaussian distribution at a parametric rate. Simulation results demonstrate the practical relevance of the formal properties of the estimators analyzed in this article.

On Computationally Efficient Learning of Exponential Family Distributions

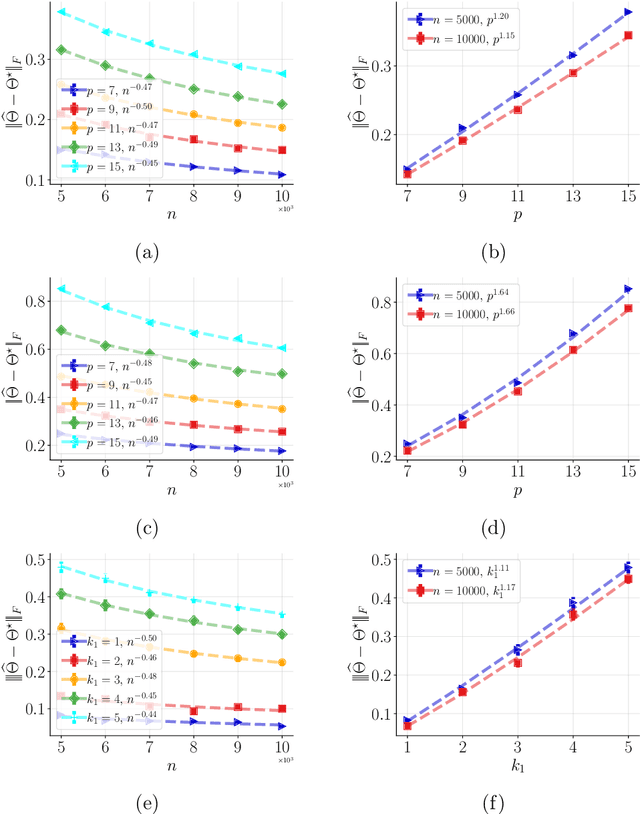
We consider the classical problem of learning, with arbitrary accuracy, the natural parameters of a $k$-parameter truncated \textit{minimal} exponential family from i.i.d. samples in a computationally and statistically efficient manner. We focus on the setting where the support as well as the natural parameters are appropriately bounded. While the traditional maximum likelihood estimator for this class of exponential family is consistent, asymptotically normal, and asymptotically efficient, evaluating it is computationally hard. In this work, we propose a novel loss function and a computationally efficient estimator that is consistent as well as asymptotically normal under mild conditions. We show that, at the population level, our method can be viewed as the maximum likelihood estimation of a re-parameterized distribution belonging to the same class of exponential family. Further, we show that our estimator can be interpreted as a solution to minimizing a particular Bregman score as well as an instance of minimizing the \textit{surrogate} likelihood. We also provide finite sample guarantees to achieve an error (in $\ell_2$-norm) of $\alpha$ in the parameter estimation with sample complexity $O({\sf poly}(k)/\alpha^2)$. Our method achives the order-optimal sample complexity of $O({\sf log}(k)/\alpha^2)$ when tailored for node-wise-sparse Markov random fields. Finally, we demonstrate the performance of our estimator via numerical experiments.

Front-door Adjustment Beyond Markov Equivalence with Limited Graph Knowledge

Causal effect estimation from data typically requires assumptions about the cause-effect relations either explicitly in the form of a causal graph structure within the Pearlian framework, or implicitly in terms of (conditional) independence statements between counterfactual variables within the potential outcomes framework. When the treatment variable and the outcome variable are confounded, front-door adjustment is an important special case where, given the graph, causal effect of the treatment on the target can be estimated using post-treatment variables. However, the exact formula for front-door adjustment depends on the structure of the graph, which is difficult to learn in practice. In this work, we provide testable conditional independence statements to compute the causal effect using front-door-like adjustment without knowing the graph under limited structural side information. We show that our method is applicable in scenarios where knowing the Markov equivalence class is not sufficient for causal effect estimation. We demonstrate the effectiveness of our method on a class of random graphs as well as real causal fairness benchmarks.

Group Fairness with Uncertainty in Sensitive Attributes

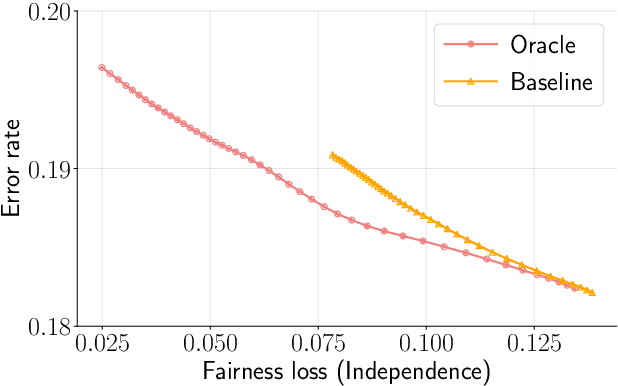
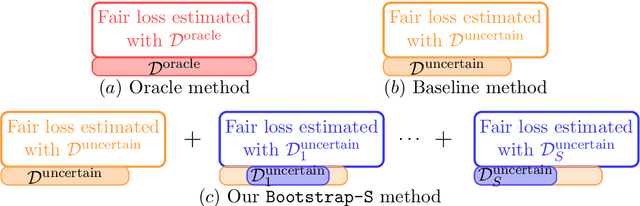
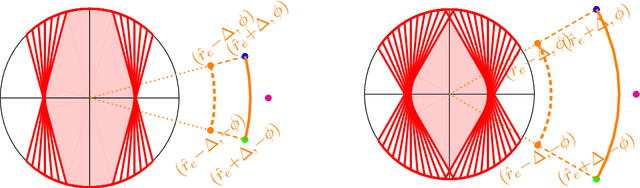
We consider learning a fair predictive model when sensitive attributes are uncertain, say, due to a limited amount of labeled data, collection bias, or privacy mechanism. We formulate the problem, for the independence notion of fairness, using the information bottleneck principle, and propose a robust optimization with respect to an uncertainty set of the sensitive attributes. As an illustrative case, we consider the joint Gaussian model and reduce the task to a quadratically constrained quadratic problem (QCQP). To ensure a strict fairness guarantee, we propose a robust QCQP and completely characterize its solution with an intuitive geometric understanding. When uncertainty arises due to limited labeled sensitive attributes, our analysis reveals the contribution of each new sample towards the optimal performance achieved with unlimited access to labeled sensitive attributes. This allows us to identify non-trivial regimes where uncertainty incurs no performance loss of the proposed algorithm while continuing to guarantee strict fairness. We also propose a bootstrap-based generic algorithm that is applicable beyond the Gaussian case. We demonstrate the value of our analysis and method on synthetic data as well as real-world classification and regression tasks.

On counterfactual inference with unobserved confounding

Given an observational study with $n$ independent but heterogeneous units and one $p$-dimensional sample per unit containing covariates, interventions, and outcomes, our goal is to learn the counterfactual distribution for each unit. We consider studies with unobserved confounding which introduces statistical biases between interventions and outcomes as well as exacerbates the heterogeneity across units. Modeling the underlying joint distribution as an exponential family and under suitable conditions, we reduce learning the $n$ unit-level counterfactual distributions to learning $n$ exponential family distributions with heterogeneous parameters and only one sample per distribution. We introduce a convex objective that pools all $n$ samples to jointly learn all $n$ parameters and provide a unit-wise mean squared error bound that scales linearly with the metric entropy of the parameter space. For example, when the parameters are $s$-sparse linear combination of $k$ known vectors, the error is $O(s\log k/p)$. En route, we derive sufficient conditions for compactly supported distributions to satisfy the logarithmic Sobolev inequality.

Optimal Compression of Locally Differentially Private Mechanisms

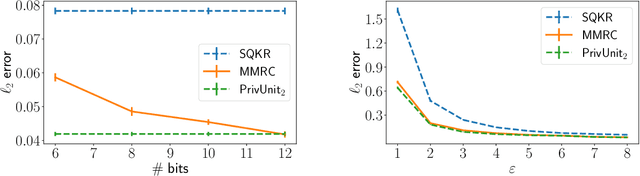
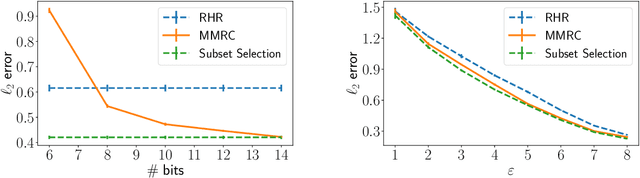
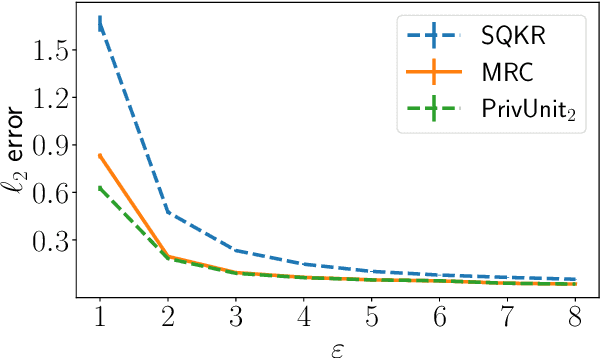
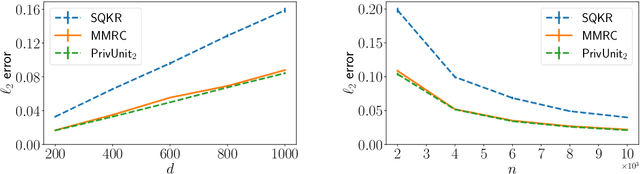
Compressing the output of \epsilon-locally differentially private (LDP) randomizers naively leads to suboptimal utility. In this work, we demonstrate the benefits of using schemes that jointly compress and privatize the data using shared randomness. In particular, we investigate a family of schemes based on Minimal Random Coding (Havasi et al., 2019) and prove that they offer optimal privacy-accuracy-communication tradeoffs. Our theoretical and empirical findings show that our approach can compress PrivUnit (Bhowmick et al., 2018) and Subset Selection (Ye et al., 2018), the best known LDP algorithms for mean and frequency estimation, to to the order of \epsilon-bits of communication while preserving their privacy and accuracy guarantees.

Selective Regression Under Fairness Criteria

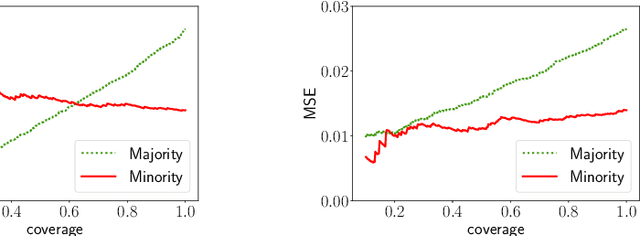
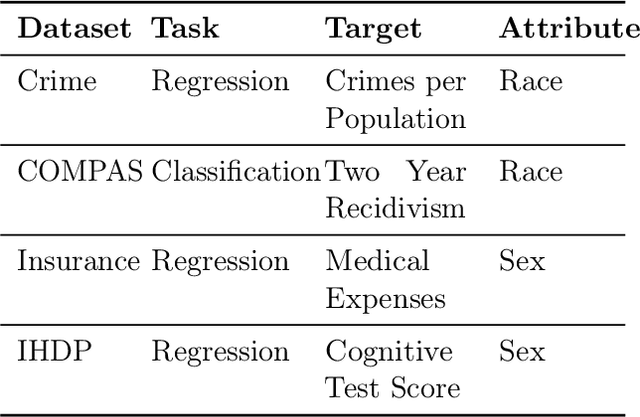
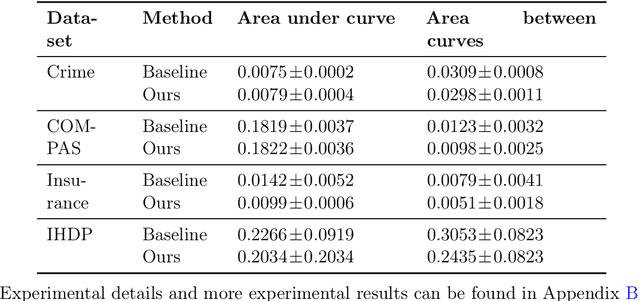
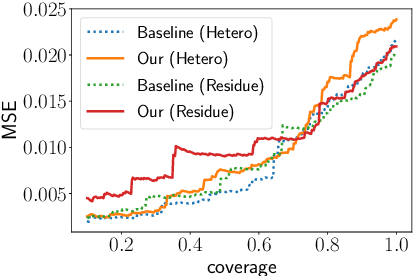
Selective regression allows abstention from prediction if the confidence to make an accurate prediction is not sufficient. In general, by allowing a reject option, one expects the performance of a regression model to increase at the cost of reducing coverage (i.e., by predicting fewer samples). However, as shown in this work, in some cases, the performance of minority group can decrease while we reduce the coverage, and thus selective regression can magnify disparities between different sensitive groups. We show that such an unwanted behavior can be avoided if we can construct features satisfying the sufficiency criterion, so that the mean prediction and the associated uncertainty are calibrated across all the groups. Further, to mitigate the disparity in the performance across groups, we introduce two approaches based on this calibration criterion: (a) by regularizing an upper bound of conditional mutual information under a Gaussian assumption and (b) by regularizing a contrastive loss for mean and uncertainty prediction. The effectiveness of these approaches are demonstrated on synthetic as well as real-world datasets.

A Computationally Efficient Method for Learning Exponential Family Distributions

We consider the question of learning the natural parameters of a $k$ parameter minimal exponential family from i.i.d. samples in a computationally and statistically efficient manner. We focus on the setting where the support as well as the natural parameters are appropriately bounded. While the traditional maximum likelihood estimator for this class of exponential family is consistent, asymptotically normal, and asymptotically efficient, evaluating it is computationally hard. In this work, we propose a computationally efficient estimator that is consistent as well as asymptotically normal under mild conditions. We provide finite sample guarantees to achieve an ($\ell_2$) error of $\alpha$ in the parameter estimation with sample complexity $O(\mathrm{poly}(k/\alpha))$ and computational complexity ${O}(\mathrm{poly}(k/\alpha))$. To establish these results, we show that, at the population level, our method can be viewed as the maximum likelihood estimation of a re-parameterized distribution belonging to the same class of exponential family.

Finding Valid Adjustments under Non-ignorability with Minimal DAG Knowledge

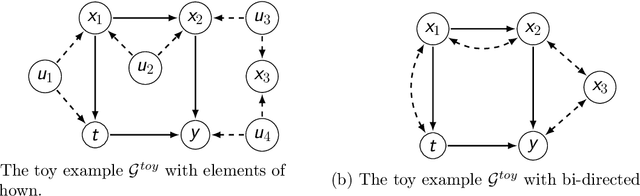
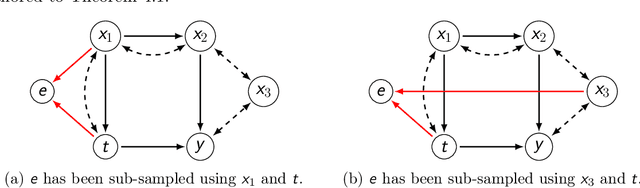
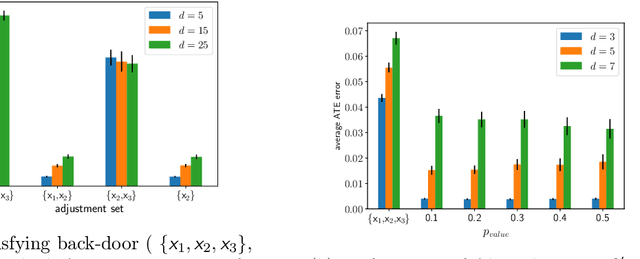
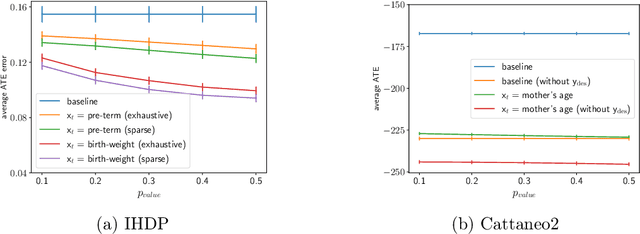
Treatment effect estimation from observational data is a fundamental problem in causal inference. There are two very different schools of thought that have tackled this problem. On the one hand, the Pearlian framework commonly assumes structural knowledge (provided by an expert) in the form of Directed Acyclic Graphs (DAGs) and provides graphical criteria such as the back-door criterion to identify the valid adjustment sets. On the other hand, the potential outcomes (PO) framework commonly assumes that all the observed features satisfy ignorability (i.e., no hidden confounding), which in general is untestable. In this work, we take steps to bridge these two frameworks. We show that even if we know only one parent of the treatment variable (provided by an expert), then quite remarkably it suffices to test a broad class of (but not all) back-door criteria. Importantly, we also cover the non-trivial case where the entire set of observed features is not ignorable (generalizing the PO framework) without requiring all the parents of the treatment variable to be observed. Our key technical idea involves a more general result -- Given a synthetic sub-sampling (or environment) variable that is a function of the parent variable, we show that an invariance test involving this sub-sampling variable is equivalent to testing a broad class of back-door criteria. We demonstrate our approach on synthetic data as well as real causal effect estimation benchmarks.