Jongha Jon Ryu
Group Fairness with Uncertainty in Sensitive Attributes
Feb 16, 2023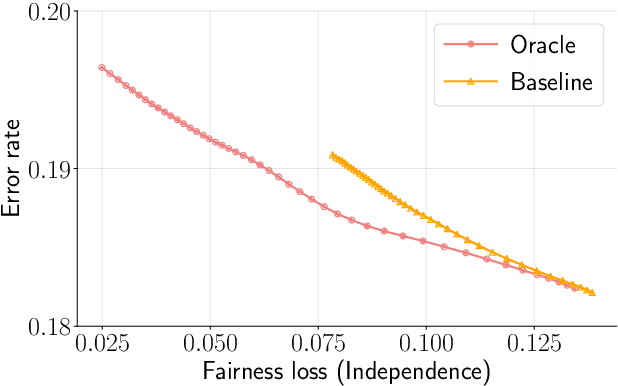

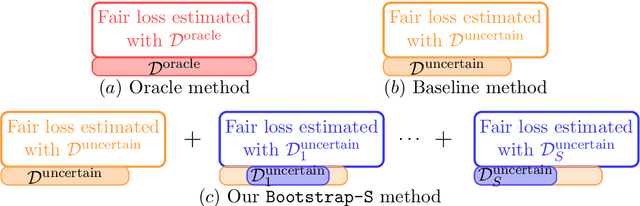
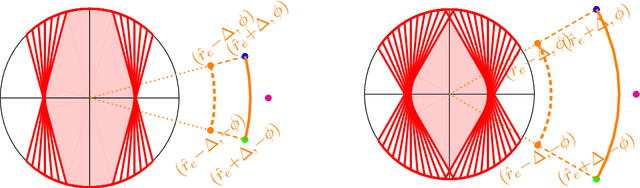
Abstract:We consider learning a fair predictive model when sensitive attributes are uncertain, say, due to a limited amount of labeled data, collection bias, or privacy mechanism. We formulate the problem, for the independence notion of fairness, using the information bottleneck principle, and propose a robust optimization with respect to an uncertainty set of the sensitive attributes. As an illustrative case, we consider the joint Gaussian model and reduce the task to a quadratically constrained quadratic problem (QCQP). To ensure a strict fairness guarantee, we propose a robust QCQP and completely characterize its solution with an intuitive geometric understanding. When uncertainty arises due to limited labeled sensitive attributes, our analysis reveals the contribution of each new sample towards the optimal performance achieved with unlimited access to labeled sensitive attributes. This allows us to identify non-trivial regimes where uncertainty incurs no performance loss of the proposed algorithm while continuing to guarantee strict fairness. We also propose a bootstrap-based generic algorithm that is applicable beyond the Gaussian case. We demonstrate the value of our analysis and method on synthetic data as well as real-world classification and regression tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge