Raaz Dwivedi
Counterfactual Forecasting For Panel Data
Nov 09, 2025Abstract:We address the challenge of forecasting counterfactual outcomes in a panel data with missing entries and temporally dependent latent factors -- a common scenario in causal inference, where estimating unobserved potential outcomes ahead of time is essential. We propose Forecasting Counterfactuals under Stochastic Dynamics (FOCUS), a method that extends traditional matrix completion methods by leveraging time series dynamics of the factors, thereby enhancing the prediction accuracy of future counterfactuals. Building upon a PCA estimator, our method accommodates both stochastic and deterministic components within the factors, and provides a flexible framework for various applications. In case of stationary autoregressive factors and under standard conditions, we derive error bounds and establish asymptotic normality of our estimator. Empirical evaluations demonstrate that our method outperforms existing benchmarks when the latent factors have an autoregressive component. We illustrate FOCUS results on HeartSteps, a mobile health study, illustrating its effectiveness in forecasting step counts for users receiving activity prompts, thereby leveraging temporal patterns in user behavior.
N$^2$: A Unified Python Package and Test Bench for Nearest Neighbor-Based Matrix Completion
Jun 04, 2025Abstract:Nearest neighbor (NN) methods have re-emerged as competitive tools for matrix completion, offering strong empirical performance and recent theoretical guarantees, including entry-wise error bounds, confidence intervals, and minimax optimality. Despite their simplicity, recent work has shown that NN approaches are robust to a range of missingness patterns and effective across diverse applications. This paper introduces N$^2$, a unified Python package and testbed that consolidates a broad class of NN-based methods through a modular, extensible interface. Built for both researchers and practitioners, N$^2$ supports rapid experimentation and benchmarking. Using this framework, we introduce a new NN variant that achieves state-of-the-art results in several settings. We also release a benchmark suite of real-world datasets, from healthcare and recommender systems to causal inference and LLM evaluation, designed to stress-test matrix completion methods beyond synthetic scenarios. Our experiments demonstrate that while classical methods excel on idealized data, NN-based techniques consistently outperform them in real-world settings.
Adaptively-weighted Nearest Neighbors for Matrix Completion
May 14, 2025Abstract:In this technical note, we introduce and analyze AWNN: an adaptively weighted nearest neighbor method for performing matrix completion. Nearest neighbor (NN) methods are widely used in missing data problems across multiple disciplines such as in recommender systems and for performing counterfactual inference in panel data settings. Prior works have shown that in addition to being very intuitive and easy to implement, NN methods enjoy nice theoretical guarantees. However, the performance of majority of the NN methods rely on the appropriate choice of the radii and the weights assigned to each member in the nearest neighbor set and despite several works on nearest neighbor methods in the past two decades, there does not exist a systematic approach of choosing the radii and the weights without relying on methods like cross-validation. AWNN addresses this challenge by judiciously balancing the bias variance trade off inherent in weighted nearest-neighbor regression. We provide theoretical guarantees for the proposed method under minimal assumptions and support the theory via synthetic experiments.
Low-Rank Thinning
Feb 17, 2025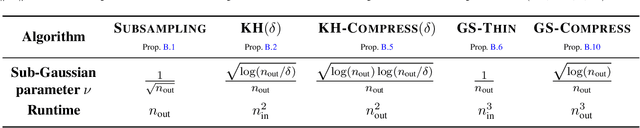

Abstract:The goal in thinning is to summarize a dataset using a small set of representative points. Remarkably, sub-Gaussian thinning algorithms like Kernel Halving and Compress can match the quality of uniform subsampling while substantially reducing the number of summary points. However, existing guarantees cover only a restricted range of distributions and kernel-based quality measures and suffer from pessimistic dimension dependence. To address these deficiencies, we introduce a new low-rank analysis of sub-Gaussian thinning that applies to any distribution and any kernel, guaranteeing high-quality compression whenever the kernel or data matrix is approximately low-rank. To demonstrate the broad applicability of the techniques, we design practical sub-Gaussian thinning approaches that improve upon the best known guarantees for approximating attention in transformers, accelerating stochastic gradient training through reordering, and distinguishing distributions in near-linear time.
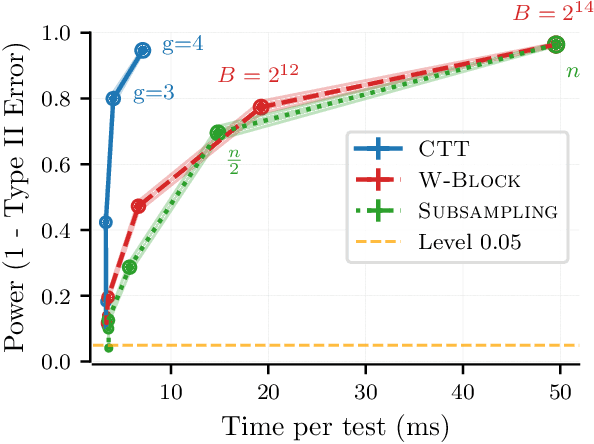
Cheap Permutation Testing
Feb 11, 2025Abstract:Permutation tests are a popular choice for distinguishing distributions and testing independence, due to their exact, finite-sample control of false positives and their minimax optimality when paired with U-statistics. However, standard permutation tests are also expensive, requiring a test statistic to be computed hundreds or thousands of times to detect a separation between distributions. In this work, we offer a simple approach to accelerate testing: group your datapoints into bins and permute only those bins. For U and V-statistics, we prove that these cheap permutation tests have two remarkable properties. First, by storing appropriate sufficient statistics, a cheap test can be run in time comparable to evaluating a single test statistic. Second, cheap permutation power closely approximates standard permutation power. As a result, cheap tests inherit the exact false positive control and minimax optimality of standard permutation tests while running in a fraction of the time. We complement these findings with improved power guarantees for standard permutation testing and experiments demonstrating the benefits of cheap permutations over standard maximum mean discrepancy (MMD), Hilbert-Schmidt independence criterion (HSIC), random Fourier feature, Wilcoxon-Mann-Whitney, cross-MMD, and cross-HSIC tests.
On adaptivity and minimax optimality of two-sided nearest neighbors
Nov 20, 2024



Abstract:Nearest neighbor (NN) algorithms have been extensively used for missing data problems in recommender systems and sequential decision-making systems. Prior theoretical analysis has established favorable guarantees for NN when the underlying data is sufficiently smooth and the missingness probabilities are lower bounded. Here we analyze NN with non-smooth non-linear functions with vast amounts of missingness. In particular, we consider matrix completion settings where the entries of the underlying matrix follow a latent non-linear factor model, with the non-linearity belonging to a \Holder function class that is less smooth than Lipschitz. Our results establish following favorable properties for a suitable two-sided NN: (1) The mean squared error (MSE) of NN adapts to the smoothness of the non-linearity, (2) under certain regularity conditions, the NN error rate matches the rate obtained by an oracle equipped with the knowledge of both the row and column latent factors, and finally (3) NN's MSE is non-trivial for a wide range of settings even when several matrix entries might be missing deterministically. We support our theoretical findings via extensive numerical simulations and a case study with data from a mobile health study, HeartSteps.
Supervised Kernel Thinning
Oct 17, 2024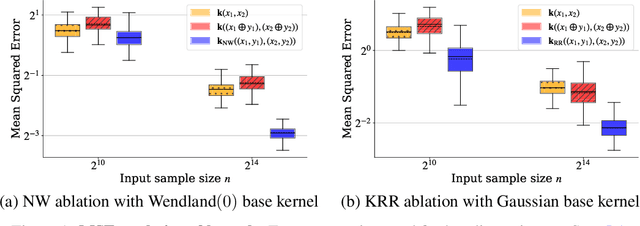
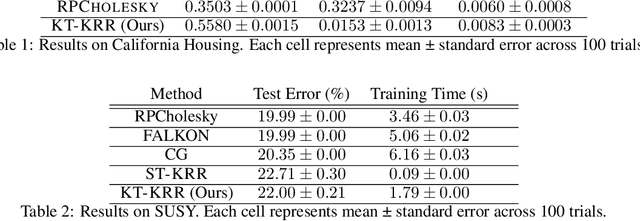
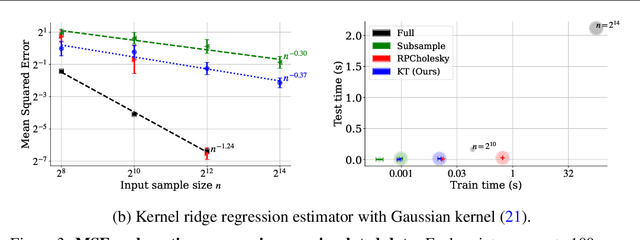
Abstract:The kernel thinning algorithm of Dwivedi & Mackey (2024) provides a better-than-i.i.d. compression of a generic set of points. By generating high-fidelity coresets of size significantly smaller than the input points, KT is known to speed up unsupervised tasks like Monte Carlo integration, uncertainty quantification, and non-parametric hypothesis testing, with minimal loss in statistical accuracy. In this work, we generalize the KT algorithm to speed up supervised learning problems involving kernel methods. Specifically, we combine two classical algorithms--Nadaraya-Watson (NW) regression or kernel smoothing, and kernel ridge regression (KRR)--with KT to provide a quadratic speed-up in both training and inference times. We show how distribution compression with KT in each setting reduces to constructing an appropriate kernel, and introduce the Kernel-Thinned NW and Kernel-Thinned KRR estimators. We prove that KT-based regression estimators enjoy significantly superior computational efficiency over the full-data estimators and improved statistical efficiency over i.i.d. subsampling of the training data. En route, we also provide a novel multiplicative error guarantee for compressing with KT. We validate our design choices with both simulations and real data experiments.
Learning Counterfactual Distributions via Kernel Nearest Neighbors
Oct 17, 2024
Abstract:Consider a setting with multiple units (e.g., individuals, cohorts, geographic locations) and outcomes (e.g., treatments, times, items), where the goal is to learn a multivariate distribution for each unit-outcome entry, such as the distribution of a user's weekly spend and engagement under a specific mobile app version. A common challenge is the prevalence of missing not at random data, where observations are available only for certain unit-outcome combinations and the observation availability can be correlated with the properties of distributions themselves, i.e., there is unobserved confounding. An additional challenge is that for any observed unit-outcome entry, we only have a finite number of samples from the underlying distribution. We tackle these two challenges by casting the problem into a novel distributional matrix completion framework and introduce a kernel based distributional generalization of nearest neighbors to estimate the underlying distributions. By leveraging maximum mean discrepancies and a suitable factor model on the kernel mean embeddings of the underlying distributions, we establish consistent recovery of the underlying distributions even when data is missing not at random and positivity constraints are violated. Furthermore, we demonstrate that our nearest neighbors approach is robust to heteroscedastic noise, provided we have access to two or more measurements for the observed unit-outcome entries, a robustness not present in prior works on nearest neighbors with single measurements.
Distributional Matrix Completion via Nearest Neighbors in the Wasserstein Space
Oct 17, 2024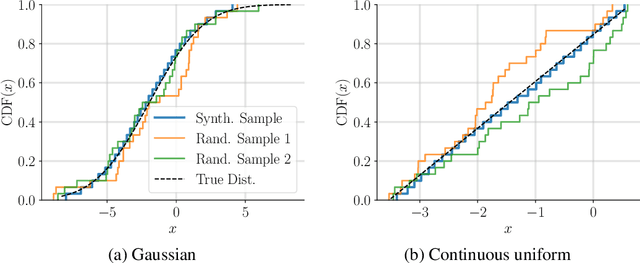
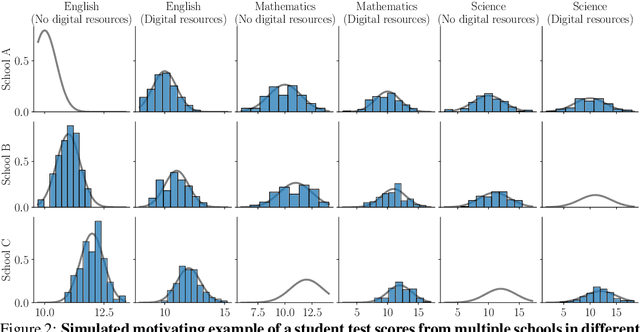
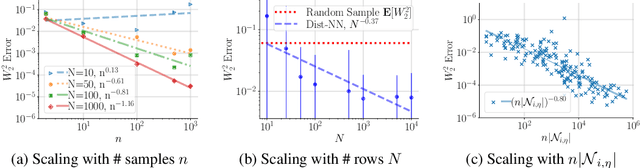
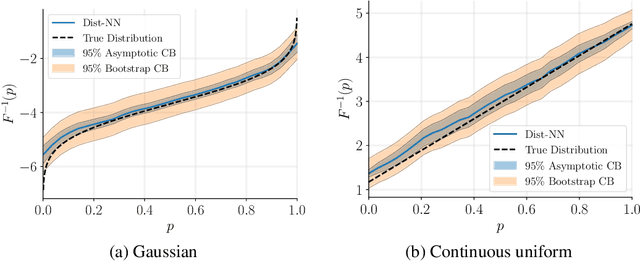
Abstract:We introduce the problem of distributional matrix completion: Given a sparsely observed matrix of empirical distributions, we seek to impute the true distributions associated with both observed and unobserved matrix entries. This is a generalization of traditional matrix completion where the observations per matrix entry are scalar valued. To do so, we utilize tools from optimal transport to generalize the nearest neighbors method to the distributional setting. Under a suitable latent factor model on probability distributions, we establish that our method recovers the distributions in the Wasserstein norm. We demonstrate through simulations that our method is able to (i) provide better distributional estimates for an entry compared to using observed samples for that entry alone, (ii) yield accurate estimates of distributional quantities such as standard deviation and value-at-risk, and (iii) inherently support heteroscedastic noise. We also prove novel asymptotic results for Wasserstein barycenters over one-dimensional distributions.
Debiased Distribution Compression
Apr 18, 2024



Abstract:Modern compression methods can summarize a target distribution $\mathbb{P}$ more succinctly than i.i.d. sampling but require access to a low-bias input sequence like a Markov chain converging quickly to $\mathbb{P}$. We introduce a new suite of compression methods suitable for compression with biased input sequences. Given $n$ points targeting the wrong distribution and quadratic time, Stein Kernel Thinning (SKT) returns $\sqrt{n}$ equal-weighted points with $\widetilde{O}(n^{-1/2})$ maximum mean discrepancy (MMD) to $\mathbb {P}$. For larger-scale compression tasks, Low-rank SKT achieves the same feat in sub-quadratic time using an adaptive low-rank debiasing procedure that may be of independent interest. For downstream tasks that support simplex or constant-preserving weights, Stein Recombination and Stein Cholesky achieve even greater parsimony, matching the guarantees of SKT with as few as $\operatorname{poly-log}(n)$ weighted points. Underlying these advances are new guarantees for the quality of simplex-weighted coresets, the spectral decay of kernel matrices, and the covering numbers of Stein kernel Hilbert spaces. In our experiments, our techniques provide succinct and accurate posterior summaries while overcoming biases due to burn-in, approximate Markov chain Monte Carlo, and tempering.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge