Distributional Matrix Completion via Nearest Neighbors in the Wasserstein Space

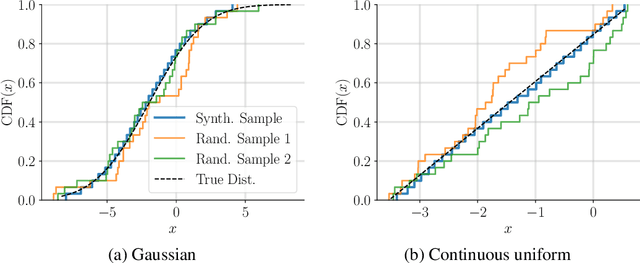
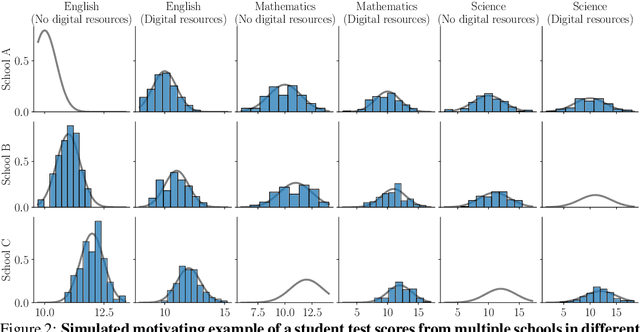
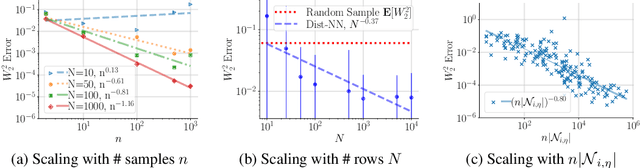
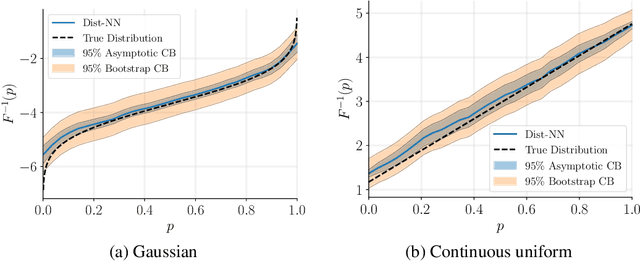
We introduce the problem of distributional matrix completion: Given a sparsely observed matrix of empirical distributions, we seek to impute the true distributions associated with both observed and unobserved matrix entries. This is a generalization of traditional matrix completion where the observations per matrix entry are scalar valued. To do so, we utilize tools from optimal transport to generalize the nearest neighbors method to the distributional setting. Under a suitable latent factor model on probability distributions, we establish that our method recovers the distributions in the Wasserstein norm. We demonstrate through simulations that our method is able to (i) provide better distributional estimates for an entry compared to using observed samples for that entry alone, (ii) yield accurate estimates of distributional quantities such as standard deviation and value-at-risk, and (iii) inherently support heteroscedastic noise. We also prove novel asymptotic results for Wasserstein barycenters over one-dimensional distributions.

Learning Counterfactual Distributions via Kernel Nearest Neighbors

Consider a setting with multiple units (e.g., individuals, cohorts, geographic locations) and outcomes (e.g., treatments, times, items), where the goal is to learn a multivariate distribution for each unit-outcome entry, such as the distribution of a user's weekly spend and engagement under a specific mobile app version. A common challenge is the prevalence of missing not at random data, where observations are available only for certain unit-outcome combinations and the observation availability can be correlated with the properties of distributions themselves, i.e., there is unobserved confounding. An additional challenge is that for any observed unit-outcome entry, we only have a finite number of samples from the underlying distribution. We tackle these two challenges by casting the problem into a novel distributional matrix completion framework and introduce a kernel based distributional generalization of nearest neighbors to estimate the underlying distributions. By leveraging maximum mean discrepancies and a suitable factor model on the kernel mean embeddings of the underlying distributions, we establish consistent recovery of the underlying distributions even when data is missing not at random and positivity constraints are violated. Furthermore, we demonstrate that our nearest neighbors approach is robust to heteroscedastic noise, provided we have access to two or more measurements for the observed unit-outcome entries, a robustness not present in prior works on nearest neighbors with single measurements.