Kyuseong Choi
GOPO: Policy Optimization using Ranked Rewards
Feb 01, 2026Abstract:Standard reinforcement learning from human feedback (RLHF) trains a reward model on pairwise preference data and then uses it for policy optimization. However, while reward models are optimized to capture relative preferences, existing policy optimization techniques rely on absolute reward magnitudes during training. In settings where the rewards are non-verifiable such as summarization, instruction following, and chat completion, this misalignment often leads to suboptimal performance. We introduce Group Ordinal Policy Optimization (GOPO), a policy optimization method that uses only the ranking of the rewards and discards their magnitudes. Our rank-based transformation of rewards provides several gains, compared to Group Relative Policy Optimization (GRPO), in settings with non-verifiable rewards: (1) consistently higher training/validation reward trajectories, (2) improved LLM-as-judge evaluations across most intermediate training steps, and (3) reaching a policy of comparable quality in substantially less training steps than GRPO. We demonstrate consistent improvements across a range of tasks and model sizes.
N$^2$: A Unified Python Package and Test Bench for Nearest Neighbor-Based Matrix Completion
Jun 04, 2025Abstract:Nearest neighbor (NN) methods have re-emerged as competitive tools for matrix completion, offering strong empirical performance and recent theoretical guarantees, including entry-wise error bounds, confidence intervals, and minimax optimality. Despite their simplicity, recent work has shown that NN approaches are robust to a range of missingness patterns and effective across diverse applications. This paper introduces N$^2$, a unified Python package and testbed that consolidates a broad class of NN-based methods through a modular, extensible interface. Built for both researchers and practitioners, N$^2$ supports rapid experimentation and benchmarking. Using this framework, we introduce a new NN variant that achieves state-of-the-art results in several settings. We also release a benchmark suite of real-world datasets, from healthcare and recommender systems to causal inference and LLM evaluation, designed to stress-test matrix completion methods beyond synthetic scenarios. Our experiments demonstrate that while classical methods excel on idealized data, NN-based techniques consistently outperform them in real-world settings.
Distributional Matrix Completion via Nearest Neighbors in the Wasserstein Space
Oct 17, 2024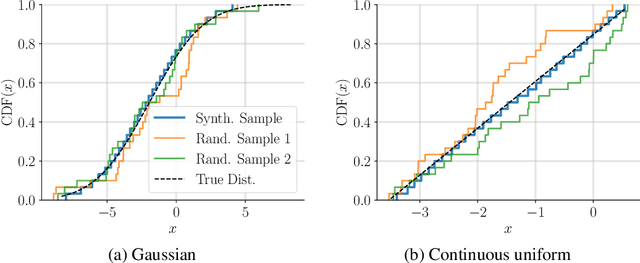
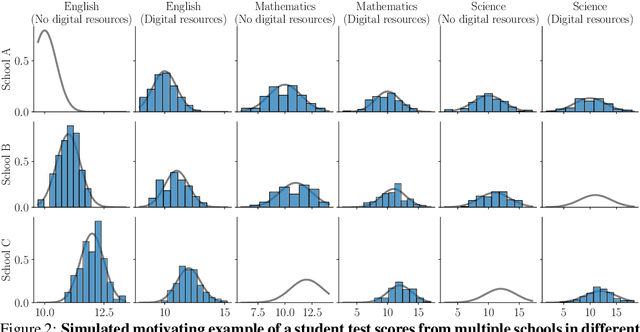
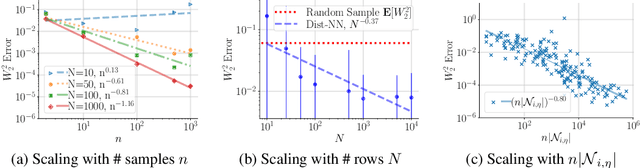
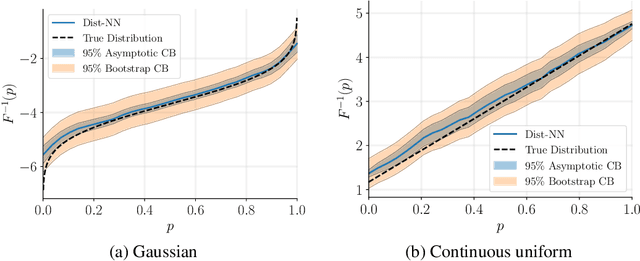
Abstract:We introduce the problem of distributional matrix completion: Given a sparsely observed matrix of empirical distributions, we seek to impute the true distributions associated with both observed and unobserved matrix entries. This is a generalization of traditional matrix completion where the observations per matrix entry are scalar valued. To do so, we utilize tools from optimal transport to generalize the nearest neighbors method to the distributional setting. Under a suitable latent factor model on probability distributions, we establish that our method recovers the distributions in the Wasserstein norm. We demonstrate through simulations that our method is able to (i) provide better distributional estimates for an entry compared to using observed samples for that entry alone, (ii) yield accurate estimates of distributional quantities such as standard deviation and value-at-risk, and (iii) inherently support heteroscedastic noise. We also prove novel asymptotic results for Wasserstein barycenters over one-dimensional distributions.
Learning Counterfactual Distributions via Kernel Nearest Neighbors
Oct 17, 2024
Abstract:Consider a setting with multiple units (e.g., individuals, cohorts, geographic locations) and outcomes (e.g., treatments, times, items), where the goal is to learn a multivariate distribution for each unit-outcome entry, such as the distribution of a user's weekly spend and engagement under a specific mobile app version. A common challenge is the prevalence of missing not at random data, where observations are available only for certain unit-outcome combinations and the observation availability can be correlated with the properties of distributions themselves, i.e., there is unobserved confounding. An additional challenge is that for any observed unit-outcome entry, we only have a finite number of samples from the underlying distribution. We tackle these two challenges by casting the problem into a novel distributional matrix completion framework and introduce a kernel based distributional generalization of nearest neighbors to estimate the underlying distributions. By leveraging maximum mean discrepancies and a suitable factor model on the kernel mean embeddings of the underlying distributions, we establish consistent recovery of the underlying distributions even when data is missing not at random and positivity constraints are violated. Furthermore, we demonstrate that our nearest neighbors approach is robust to heteroscedastic noise, provided we have access to two or more measurements for the observed unit-outcome entries, a robustness not present in prior works on nearest neighbors with single measurements.
Supervised Kernel Thinning
Oct 17, 2024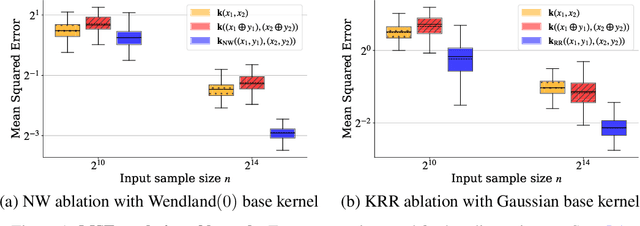
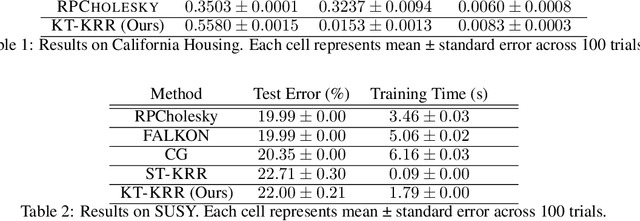
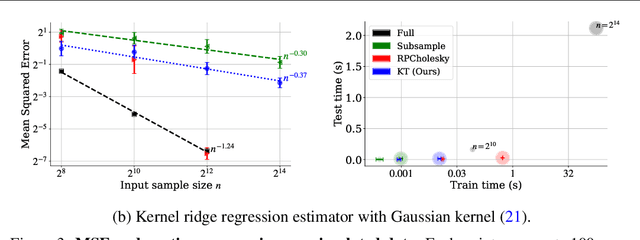
Abstract:The kernel thinning algorithm of Dwivedi & Mackey (2024) provides a better-than-i.i.d. compression of a generic set of points. By generating high-fidelity coresets of size significantly smaller than the input points, KT is known to speed up unsupervised tasks like Monte Carlo integration, uncertainty quantification, and non-parametric hypothesis testing, with minimal loss in statistical accuracy. In this work, we generalize the KT algorithm to speed up supervised learning problems involving kernel methods. Specifically, we combine two classical algorithms--Nadaraya-Watson (NW) regression or kernel smoothing, and kernel ridge regression (KRR)--with KT to provide a quadratic speed-up in both training and inference times. We show how distribution compression with KT in each setting reduces to constructing an appropriate kernel, and introduce the Kernel-Thinned NW and Kernel-Thinned KRR estimators. We prove that KT-based regression estimators enjoy significantly superior computational efficiency over the full-data estimators and improved statistical efficiency over i.i.d. subsampling of the training data. En route, we also provide a novel multiplicative error guarantee for compressing with KT. We validate our design choices with both simulations and real data experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge