ORCA-bench: How Ready Are Language Model Agents for Oncall?

Large language models can write, patch, and search code, but oncall root cause analysis (RCA) demands something different: reasoning over noisy metrics, logs, traces, and source code, starting from ambiguous user-facing reports, often hours after the incident began. We introduce ORCA-bench, a benchmark that puts general-purpose coding agents in a production-fidelity oncall setting. ORCA-bench pairs a live OpenTelemetry-instrumented microservice system--exposing six days of metrics, logs, and traces through real telemetry interfaces (Prometheus, Jaeger, and OpenSearch via Grafana) and full source-code access--with 1,079 RCA tasks that systematically vary report specificity, time-to-detection, and co-occurring fault scenarios. Ground-truth symptoms are curated and signed off by expert SREs, and our LLM-as-judge is independently re-scored by humans (Cohen's $κ_w=0.90$). Across five frontier agents, the best RCA Accuracy is 25.3% on Medium-difficulty tasks (the realistic-input setting) and 10.0% on Hard--a gap that remains even with Claude Fable 5. The weakest model hallucinates an implausible root cause in 40% of incident reports, and removing source-code access degrades every metric. Crucially, these are performances on a curated 50 GB / six-day testbed with tasks investigated in isolation on a system whose code and instrumentation are public. Since real production systems are order of magnitudes larger, more dynamic, and more idiosyncratic, the gap we report is a lower bound on the engineering investment required before frontier coding agents can be safely entrusted with production reliability. We release the public set at https://hub.harborframework.com/datasets/orca-bench/ORCA-bench.

Express Language Modeling

We introduce a new tool, Express, for converting a non-causal attention approximation into a causal approximation with matching approximation guarantees. When combined with the state-of-the-art Thinformer approximation, Express improves upon the best known causal attention guarantees, delivering $\log^{3/2}(n)/s$ approximation error with only $O(s)$ memory and $O(s^2 \log^2(n))$ compression overhead for a sequence of length $n$. We pair these developments with an efficient I/O-aware Triton implementation, demonstrate substantial speedups over FlashAttention 2, and use Express to overcome four resource bottlenecks in the language modeling pipeline: long-context prefill, KV cache compression, long-form memory-constrained decoding, and long-form compute-constrained decoding.

Learning from Synthetic Data Improves Multi-hop Reasoning

Reinforcement Learning (RL) has been shown to significantly boost reasoning capabilities of large language models (LLMs) in math, coding, and multi-hop reasoning tasks. However, RL fine-tuning requires abundant high-quality verifiable data, often sourced from human annotations, generated from frontier LLMs, or scored by LLM-based verifiers. All three have considerable limitations: human-annotated datasets are small and expensive to curate, LLM-generated data is hallucination-prone and costly, and LLM-based verifiers are inaccurate and slow. In this work, we investigate a cheaper alternative: RL fine-tuning on rule-generated synthetic data for multi-hop reasoning tasks. We discover that LLMs fine-tuned on synthetic data perform significantly better on popular real-world question-answering benchmarks, despite the synthetic data containing only fictional knowledge. On stratifying performance by question difficulty, we find that synthetic data teaches LLMs to compose knowledge -- a fundamental and generalizable reasoning skill. Our work highlights rule-generated synthetic reasoning data as a free and scalable resource to improve LLM reasoning capabilities.

Memento: Note-Taking for Your Future Self

Large language models (LLMs) excel at reasoning-only tasks, but struggle when reasoning must be tightly coupled with retrieval, as in multi-hop question answering. To overcome these limitations, we introduce a prompting strategy that first decomposes a complex question into smaller steps, then dynamically constructs a database of facts using LLMs, and finally pieces these facts together to solve the question. We show how this three-stage strategy, which we call Memento, can boost the performance of existing prompting strategies across diverse settings. On the 9-step PhantomWiki benchmark, Memento doubles the performance of chain-of-thought (CoT) when all information is provided in context. On the open-domain version of 2WikiMultiHopQA, CoT-RAG with Memento improves over vanilla CoT-RAG by more than 20 F1 percentage points and over the multi-hop RAG baseline, IRCoT, by more than 13 F1 percentage points. On the challenging MuSiQue dataset, Memento improves ReAct by more than 3 F1 percentage points, demonstrating its utility in agentic settings.

N$^2$: A Unified Python Package and Test Bench for Nearest Neighbor-Based Matrix Completion

Nearest neighbor (NN) methods have re-emerged as competitive tools for matrix completion, offering strong empirical performance and recent theoretical guarantees, including entry-wise error bounds, confidence intervals, and minimax optimality. Despite their simplicity, recent work has shown that NN approaches are robust to a range of missingness patterns and effective across diverse applications. This paper introduces N$^2$, a unified Python package and testbed that consolidates a broad class of NN-based methods through a modular, extensible interface. Built for both researchers and practitioners, N$^2$ supports rapid experimentation and benchmarking. Using this framework, we introduce a new NN variant that achieves state-of-the-art results in several settings. We also release a benchmark suite of real-world datasets, from healthcare and recommender systems to causal inference and LLM evaluation, designed to stress-test matrix completion methods beyond synthetic scenarios. Our experiments demonstrate that while classical methods excel on idealized data, NN-based techniques consistently outperform them in real-world settings.

PhantomWiki: On-Demand Datasets for Reasoning and Retrieval Evaluation

High-quality benchmarks are essential for evaluating reasoning and retrieval capabilities of large language models (LLMs). However, curating datasets for this purpose is not a permanent solution as they are prone to data leakage and inflated performance results. To address these challenges, we propose PhantomWiki: a pipeline to generate unique, factually consistent document corpora with diverse question-answer pairs. Unlike prior work, PhantomWiki is neither a fixed dataset, nor is it based on any existing data. Instead, a new PhantomWiki instance is generated on demand for each evaluation. We vary the question difficulty and corpus size to disentangle reasoning and retrieval capabilities respectively, and find that PhantomWiki datasets are surprisingly challenging for frontier LLMs. Thus, we contribute a scalable and data leakage-resistant framework for disentangled evaluation of reasoning, retrieval, and tool-use abilities. Our code is available at https://github.com/kilian-group/phantom-wiki.

Low-Rank Thinning

The goal in thinning is to summarize a dataset using a small set of representative points. Remarkably, sub-Gaussian thinning algorithms like Kernel Halving and Compress can match the quality of uniform subsampling while substantially reducing the number of summary points. However, existing guarantees cover only a restricted range of distributions and kernel-based quality measures and suffer from pessimistic dimension dependence. To address these deficiencies, we introduce a new low-rank analysis of sub-Gaussian thinning that applies to any distribution and any kernel, guaranteeing high-quality compression whenever the kernel or data matrix is approximately low-rank. To demonstrate the broad applicability of the techniques, we design practical sub-Gaussian thinning approaches that improve upon the best known guarantees for approximating attention in transformers, accelerating stochastic gradient training through reordering, and distinguishing distributions in near-linear time.

Supervised Kernel Thinning

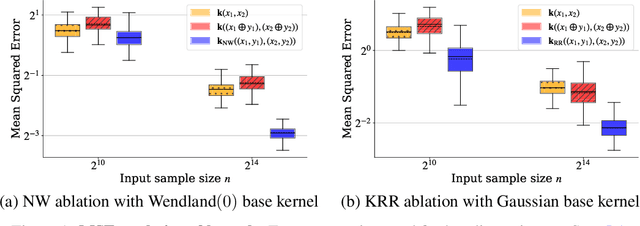
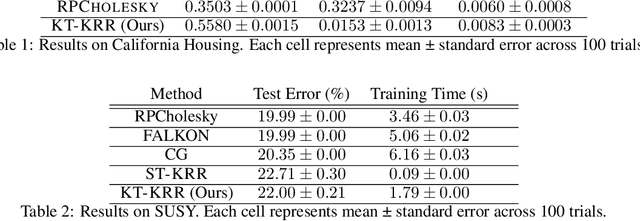
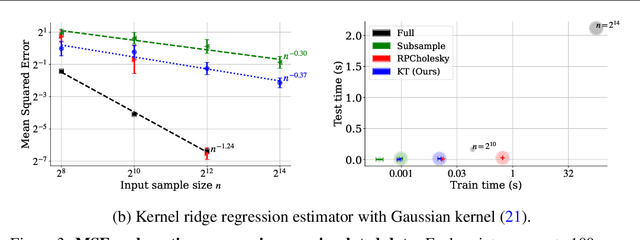
The kernel thinning algorithm of Dwivedi & Mackey (2024) provides a better-than-i.i.d. compression of a generic set of points. By generating high-fidelity coresets of size significantly smaller than the input points, KT is known to speed up unsupervised tasks like Monte Carlo integration, uncertainty quantification, and non-parametric hypothesis testing, with minimal loss in statistical accuracy. In this work, we generalize the KT algorithm to speed up supervised learning problems involving kernel methods. Specifically, we combine two classical algorithms--Nadaraya-Watson (NW) regression or kernel smoothing, and kernel ridge regression (KRR)--with KT to provide a quadratic speed-up in both training and inference times. We show how distribution compression with KT in each setting reduces to constructing an appropriate kernel, and introduce the Kernel-Thinned NW and Kernel-Thinned KRR estimators. We prove that KT-based regression estimators enjoy significantly superior computational efficiency over the full-data estimators and improved statistical efficiency over i.i.d. subsampling of the training data. En route, we also provide a novel multiplicative error guarantee for compressing with KT. We validate our design choices with both simulations and real data experiments.

Virtual CNN Branching: Efficient Feature Ensemble for Person Re-Identification

In this paper we introduce an ensemble method for convolutional neural network (CNN), called "virtual branching," which can be implemented with nearly no additional parameters and computation on top of standard CNNs. We propose our method in the context of person re-identification (re-ID). Our CNN model consists of shared bottom layers, followed by "virtual" branches, where neurons from a block of regular convolutional and fully-connected layers are partitioned into multiple sets. Each virtual branch is trained with different data to specialize in different aspects, e.g., a specific body region or pose orientation. In this way, robust ensemble representations are obtained against human body misalignment, deformations, or variations in viewing angles, at nearly no any additional cost. The proposed method achieves competitive performance on multiple person re-ID benchmark datasets, including Market-1501, CUHK03, and DukeMTMC-reID.