Johannes Balle
Optimal Compression of Locally Differentially Private Mechanisms
Oct 29, 2021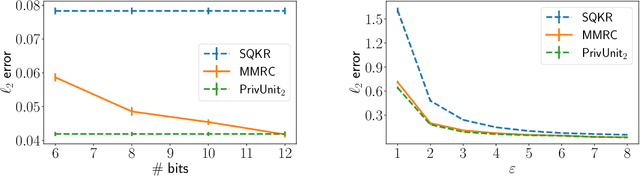
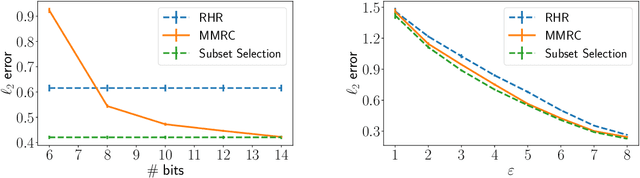
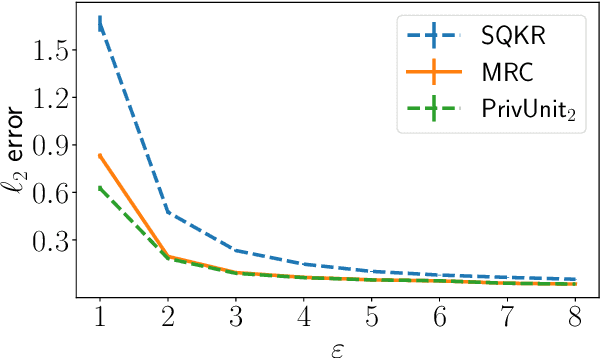
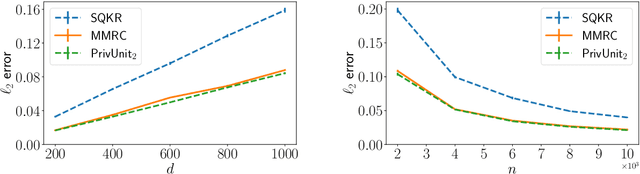
Abstract:Compressing the output of \epsilon-locally differentially private (LDP) randomizers naively leads to suboptimal utility. In this work, we demonstrate the benefits of using schemes that jointly compress and privatize the data using shared randomness. In particular, we investigate a family of schemes based on Minimal Random Coding (Havasi et al., 2019) and prove that they offer optimal privacy-accuracy-communication tradeoffs. Our theoretical and empirical findings show that our approach can compress PrivUnit (Bhowmick et al., 2018) and Subset Selection (Ye et al., 2018), the best known LDP algorithms for mean and frequency estimation, to to the order of \epsilon-bits of communication while preserving their privacy and accuracy guarantees.
Accelerating Training of Deep Neural Networks with a Standardization Loss
Mar 03, 2019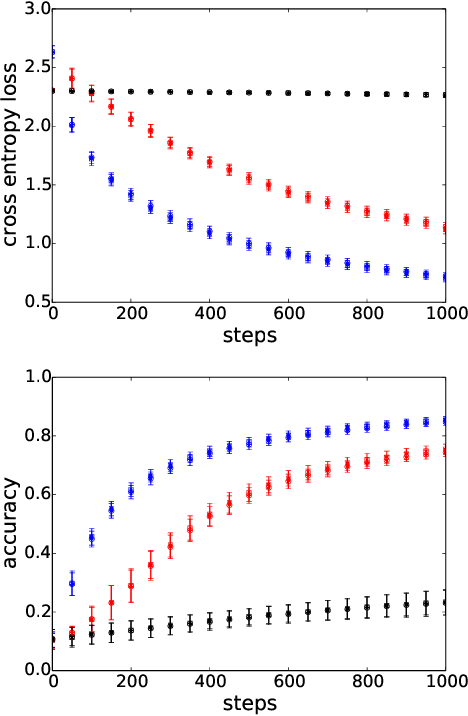
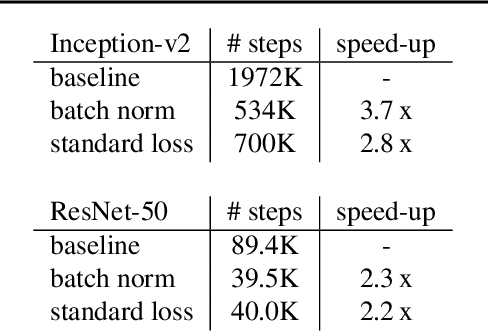
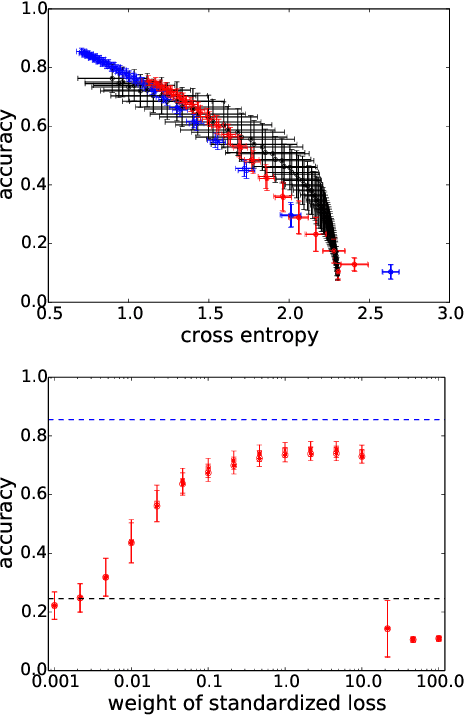
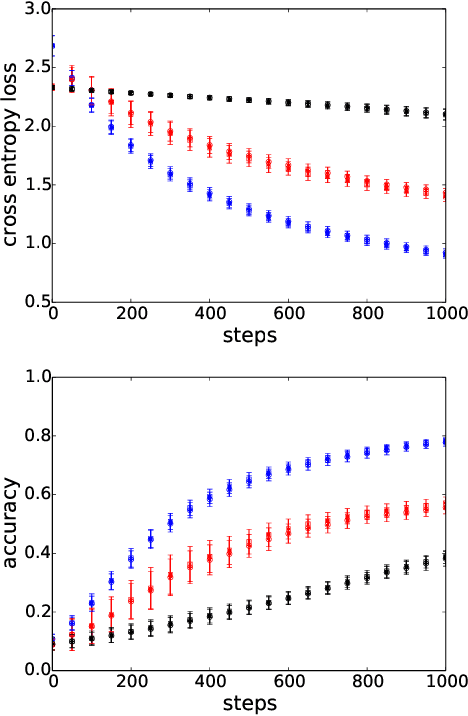
Abstract:A significant advance in accelerating neural network training has been the development of normalization methods, permitting the training of deep models both faster and with better accuracy. These advances come with practical challenges: for instance, batch normalization ties the prediction of individual examples with other examples within a batch, resulting in a network that is heavily dependent on batch size. Layer normalization and group normalization are data-dependent and thus must be continually used, even at test-time. To address the issues that arise from using explicit normalization techniques, we propose to replace existing normalization methods with a simple, secondary objective loss that we term a standardization loss. This formulation is flexible and robust across different batch sizes and surprisingly, this secondary objective accelerates learning on the primary training objective. Because it is a training loss, it is simply removed at test-time, and no further effort is needed to maintain normalized activations. We find that a standardization loss accelerates training on both small- and large-scale image classification experiments, works with a variety of architectures, and is largely robust to training across different batch sizes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge