Differentially Private Adaptation of Diffusion Models via Noisy Aggregated Embeddings

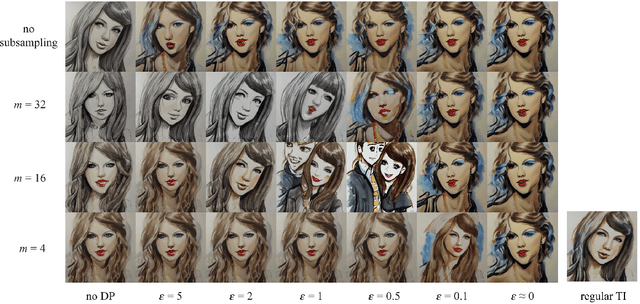
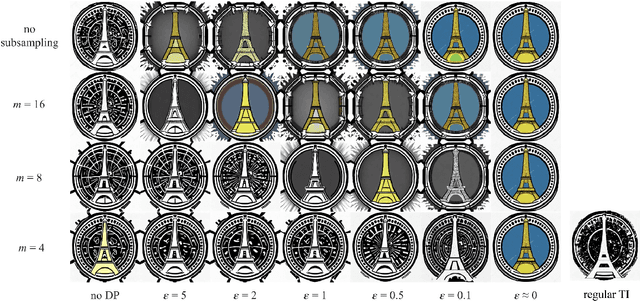
We introduce novel methods for adapting diffusion models under differential privacy (DP) constraints, enabling privacy-preserving style and content transfer without fine-tuning. Traditional approaches to private adaptation, such as DP-SGD, incur significant computational overhead and degrade model performance when applied to large, complex models. Our approach instead leverages embedding-based techniques: Universal Guidance and Textual Inversion (TI), adapted with differentially private mechanisms. We apply these methods to Stable Diffusion for style adaptation using two private datasets: a collection of artworks by a single artist and pictograms from the Paris 2024 Olympics. Experimental results show that the TI-based adaptation achieves superior fidelity in style transfer, even under strong privacy guarantees, while both methods maintain high privacy resilience by employing calibrated noise and subsampling strategies. Our findings demonstrate a feasible and efficient pathway for privacy-preserving diffusion model adaptation, balancing data protection with the fidelity of generated images, and offer insights into embedding-driven methods for DP in generative AI applications.

Randomization Techniques to Mitigate the Risk of Copyright Infringement

In this paper, we investigate potential randomization approaches that can complement current practices of input-based methods (such as licensing data and prompt filtering) and output-based methods (such as recitation checker, license checker, and model-based similarity score) for copyright protection. This is motivated by the inherent ambiguity of the rules that determine substantial similarity in copyright precedents. Given that there is no quantifiable measure of substantial similarity that is agreed upon, complementary approaches can potentially further decrease liability. Similar randomized approaches, such as differential privacy, have been successful in mitigating privacy risks. This document focuses on the technical and research perspective on mitigating copyright violation and hence is not confidential. After investigating potential solutions and running numerical experiments, we concluded that using the notion of Near Access-Freeness (NAF) to measure the degree of substantial similarity is challenging, and the standard approach of training a Differentially Private (DP) model costs significantly when used to ensure NAF. Alternative approaches, such as retrieval models, might provide a more controllable scheme for mitigating substantial similarity.

Universal Exact Compression of Differentially Private Mechanisms

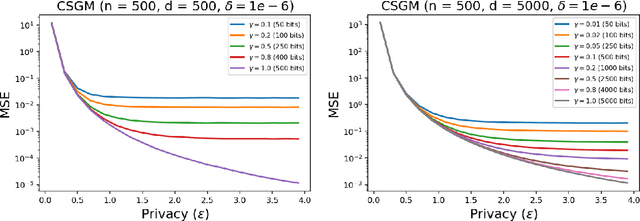
To reduce the communication cost of differential privacy mechanisms, we introduce a novel construction, called Poisson private representation (PPR), designed to compress and simulate any local randomizer while ensuring local differential privacy. Unlike previous simulation-based local differential privacy mechanisms, PPR exactly preserves the joint distribution of the data and the output of the original local randomizer. Hence, the PPR-compressed privacy mechanism retains all desirable statistical properties of the original privacy mechanism such as unbiasedness and Gaussianity. Moreover, PPR achieves a compression size within a logarithmic gap from the theoretical lower bound. Using the PPR, we give a new order-wise trade-off between communication, accuracy, central and local differential privacy for distributed mean estimation. Experiment results on distributed mean estimation show that PPR consistently gives a better trade-off between communication, accuracy and central differential privacy compared to the coordinate subsampled Gaussian mechanism, while also providing local differential privacy.

Improved Communication-Privacy Trade-offs in $L_2$ Mean Estimation under Streaming Differential Privacy

We study $L_2$ mean estimation under central differential privacy and communication constraints, and address two key challenges: firstly, existing mean estimation schemes that simultaneously handle both constraints are usually optimized for $L_\infty$ geometry and rely on random rotation or Kashin's representation to adapt to $L_2$ geometry, resulting in suboptimal leading constants in mean square errors (MSEs); secondly, schemes achieving order-optimal communication-privacy trade-offs do not extend seamlessly to streaming differential privacy (DP) settings (e.g., tree aggregation or matrix factorization), rendering them incompatible with DP-FTRL type optimizers. In this work, we tackle these issues by introducing a novel privacy accounting method for the sparsified Gaussian mechanism that incorporates the randomness inherent in sparsification into the DP noise. Unlike previous approaches, our accounting algorithm directly operates in $L_2$ geometry, yielding MSEs that fast converge to those of the uncompressed Gaussian mechanism. Additionally, we extend the sparsification scheme to the matrix factorization framework under streaming DP and provide a precise accountant tailored for DP-FTRL type optimizers. Empirically, our method demonstrates at least a 100x improvement of compression for DP-SGD across various FL tasks.

Differentially Private Decoupled Graph Convolutions for Multigranular Topology Protection

Graph learning methods, such as Graph Neural Networks (GNNs) based on graph convolutions, are highly successful in solving real-world learning problems involving graph-structured data. However, graph learning methods expose sensitive user information and interactions not only through their model parameters but also through their model predictions. Consequently, standard Differential Privacy (DP) techniques that merely offer model weight privacy are inadequate. This is especially the case for node predictions that leverage neighboring node attributes directly via graph convolutions that create additional risks of privacy leakage. To address this problem, we introduce Graph Differential Privacy (GDP), a new formal DP framework tailored to graph learning settings that ensures both provably private model parameters and predictions. Furthermore, since there may be different privacy requirements for the node attributes and graph structure, we introduce a novel notion of relaxed node-level data adjacency. This relaxation can be used for establishing guarantees for different degrees of graph topology privacy while maintaining node attribute privacy. Importantly, this relaxation reveals a useful trade-off between utility and topology privacy for graph learning methods. In addition, our analysis of GDP reveals that existing DP-GNNs fail to exploit this trade-off due to the complex interplay between graph topology and attribute data in standard graph convolution designs. To mitigate this problem, we introduce the Differentially Private Decoupled Graph Convolution (DPDGC) model, which benefits from decoupled graph convolution while providing GDP guarantees. Extensive experiments on seven node classification benchmarking datasets demonstrate the superior privacy-utility trade-off of DPDGC over existing DP-GNNs based on standard graph convolution design.

Training generative models from privatized data

Local differential privacy (LDP) is a powerful method for privacy-preserving data collection. In this paper, we develop a framework for training Generative Adversarial Networks (GAN) on differentially privatized data. We show that entropic regularization of the Wasserstein distance -- a popular regularization method in the literature that has been often leveraged for its computational benefits -- can be used to denoise the data distribution when data is privatized by common additive noise mechanisms, such as Laplace and Gaussian. This combination uniquely enables the mitigation of both the regularization bias and the effects of privatization noise, thereby enhancing the overall efficacy of the model. We analyse the proposed method, provide sample complexity results and experimental evidence to support its efficacy.

Exact Optimality of Communication-Privacy-Utility Tradeoffs in Distributed Mean Estimation

We study the mean estimation problem under communication and local differential privacy constraints. While previous work has proposed \emph{order}-optimal algorithms for the same problem (i.e., asymptotically optimal as we spend more bits), \emph{exact} optimality (in the non-asymptotic setting) still has not been achieved. In this work, we take a step towards characterizing the \emph{exact}-optimal approach in the presence of shared randomness (a random variable shared between the server and the user) and identify several necessary conditions for \emph{exact} optimality. We prove that one of the necessary conditions is to utilize a rotationally symmetric shared random codebook. Based on this, we propose a randomization mechanism where the codebook is a randomly rotated simplex -- satisfying the necessary properties of the \emph{exact}-optimal codebook. The proposed mechanism is based on a $k$-closest encoding which we prove to be \emph{exact}-optimal for the randomly rotated simplex codebook.

Privacy Amplification via Compression: Achieving the Optimal Privacy-Accuracy-Communication Trade-off in Distributed Mean Estimation

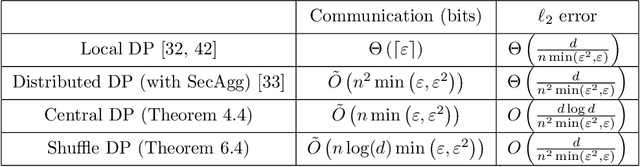
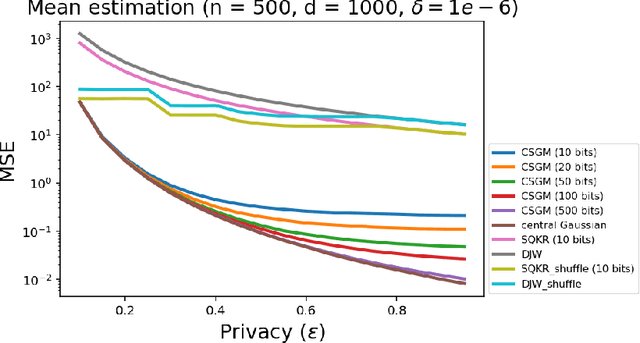
Privacy and communication constraints are two major bottlenecks in federated learning (FL) and analytics (FA). We study the optimal accuracy of mean and frequency estimation (canonical models for FL and FA respectively) under joint communication and $(\varepsilon, \delta)$-differential privacy (DP) constraints. We show that in order to achieve the optimal error under $(\varepsilon, \delta)$-DP, it is sufficient for each client to send $\Theta\left( n \min\left(\varepsilon, \varepsilon^2\right)\right)$ bits for FL and $\Theta\left(\log\left( n\min\left(\varepsilon, \varepsilon^2\right) \right)\right)$ bits for FA to the server, where $n$ is the number of participating clients. Without compression, each client needs $O(d)$ bits and $\log d$ bits for the mean and frequency estimation problems respectively (where $d$ corresponds to the number of trainable parameters in FL or the domain size in FA), which means that we can get significant savings in the regime $ n \min\left(\varepsilon, \varepsilon^2\right) = o(d)$, which is often the relevant regime in practice. Our algorithms leverage compression for privacy amplification: when each client communicates only partial information about its sample, we show that privacy can be amplified by randomly selecting the part contributed by each client.

The Fundamental Price of Secure Aggregation in Differentially Private Federated Learning

We consider the problem of training a $d$ dimensional model with distributed differential privacy (DP) where secure aggregation (SecAgg) is used to ensure that the server only sees the noisy sum of $n$ model updates in every training round. Taking into account the constraints imposed by SecAgg, we characterize the fundamental communication cost required to obtain the best accuracy achievable under $\varepsilon$ central DP (i.e. under a fully trusted server and no communication constraints). Our results show that $\tilde{O}\left( \min(n^2\varepsilon^2, d) \right)$ bits per client are both sufficient and necessary, and this fundamental limit can be achieved by a linear scheme based on sparse random projections. This provides a significant improvement relative to state-of-the-art SecAgg distributed DP schemes which use $\tilde{O}(d\log(d/\varepsilon^2))$ bits per client. Empirically, we evaluate our proposed scheme on real-world federated learning tasks. We find that our theoretical analysis is well matched in practice. In particular, we show that we can reduce the communication cost significantly to under $1.2$ bits per parameter in realistic privacy settings without decreasing test-time performance. Our work hence theoretically and empirically specifies the fundamental price of using SecAgg.

Optimal Compression of Locally Differentially Private Mechanisms

Compressing the output of \epsilon-locally differentially private (LDP) randomizers naively leads to suboptimal utility. In this work, we demonstrate the benefits of using schemes that jointly compress and privatize the data using shared randomness. In particular, we investigate a family of schemes based on Minimal Random Coding (Havasi et al., 2019) and prove that they offer optimal privacy-accuracy-communication tradeoffs. Our theoretical and empirical findings show that our approach can compress PrivUnit (Bhowmick et al., 2018) and Subset Selection (Ye et al., 2018), the best known LDP algorithms for mean and frequency estimation, to to the order of \epsilon-bits of communication while preserving their privacy and accuracy guarantees.