SeMAnD: Self-Supervised Anomaly Detection in Multimodal Geospatial Datasets

We propose a Self-supervised Anomaly Detection technique, called SeMAnD, to detect geometric anomalies in Multimodal geospatial datasets. Geospatial data comprises of acquired and derived heterogeneous data modalities that we transform to semantically meaningful, image-like tensors to address the challenges of representation, alignment, and fusion of multimodal data. SeMAnD is comprised of (i) a simple data augmentation strategy, called RandPolyAugment, capable of generating diverse augmentations of vector geometries, and (ii) a self-supervised training objective with three components that incentivize learning representations of multimodal data that are discriminative to local changes in one modality which are not corroborated by the other modalities. Detecting local defects is crucial for geospatial anomaly detection where even small anomalies (e.g., shifted, incorrectly connected, malformed, or missing polygonal vector geometries like roads, buildings, landcover, etc.) are detrimental to the experience and safety of users of geospatial applications like mapping, routing, search, and recommendation systems. Our empirical study on test sets of different types of real-world geometric geospatial anomalies across 3 diverse geographical regions demonstrates that SeMAnD is able to detect real-world defects and outperforms domain-agnostic anomaly detection strategies by 4.8-19.7% as measured using anomaly classification AUC. We also show that model performance increases (i) up to 20.4% as the number of input modalities increase and (ii) up to 22.9% as the diversity and strength of training data augmentations increase.

ParGANDA: Making Synthetic Pedestrians A Reality For Object Detection

Object detection is the key technique to a number of Computer Vision applications, but it often requires large amounts of annotated data to achieve decent results. Moreover, for pedestrian detection specifically, the collected data might contain some personally identifiable information (PII), which is highly restricted in many countries. This label intensive and privacy concerning task has recently led to an increasing interest in training the detection models using synthetically generated pedestrian datasets collected with a photo-realistic video game engine. The engine is able to generate unlimited amounts of data with precise and consistent annotations, which gives potential for significant gains in the real-world applications. However, the use of synthetic data for training introduces a synthetic-to-real domain shift aggravating the final performance. To close the gap between the real and synthetic data, we propose to use a Generative Adversarial Network (GAN), which performsparameterized unpaired image-to-image translation to generate more realistic images. The key benefit of using the GAN is its intrinsic preference of low-level changes to geometric ones, which means annotations of a given synthetic image remain accurate even after domain translation is performed thus eliminating the need for labeling real data. We extensively experimented with the proposed method using MOTSynth dataset to train and MOT17 and MOT20 detection datasets to test, with experimental results demonstrating the effectiveness of this method. Our approach not only produces visually plausible samples but also does not require any labels of the real domain thus making it applicable to the variety of downstream tasks.

Training generative models from privatized data

Local differential privacy (LDP) is a powerful method for privacy-preserving data collection. In this paper, we develop a framework for training Generative Adversarial Networks (GAN) on differentially privatized data. We show that entropic regularization of the Wasserstein distance -- a popular regularization method in the literature that has been often leveraged for its computational benefits -- can be used to denoise the data distribution when data is privatized by common additive noise mechanisms, such as Laplace and Gaussian. This combination uniquely enables the mitigation of both the regularization bias and the effects of privatization noise, thereby enhancing the overall efficacy of the model. We analyse the proposed method, provide sample complexity results and experimental evidence to support its efficacy.

Understanding Entropic Regularization in GANs

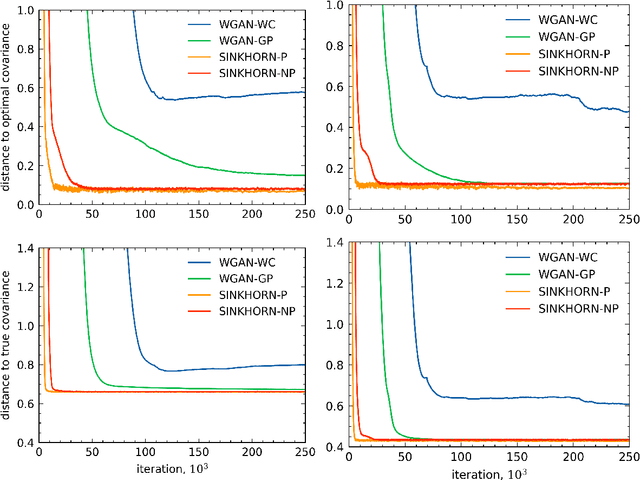
Generative Adversarial Networks are a popular method for learning distributions from data by modeling the target distribution as a function of a known distribution. The function, often referred to as the generator, is optimized to minimize a chosen distance measure between the generated and target distributions. One commonly used measure for this purpose is the Wasserstein distance. However, Wasserstein distance is hard to compute and optimize, and in practice entropic regularization techniques are used to improve numerical convergence. The influence of regularization on the learned solution, however, remains not well-understood. In this paper, we study how several popular entropic regularizations of Wasserstein distance impact the solution in a simple benchmark setting where the generator is linear and the target distribution is high-dimensional Gaussian. We show that entropy regularization promotes the solution sparsification, while replacing the Wasserstein distance with the Sinkhorn divergence recovers the unregularized solution. Both regularization techniques remove the curse of dimensionality suffered by Wasserstein distance. We show that the optimal generator can be learned to accuracy $\epsilon$ with $O(1/\epsilon^2)$ samples from the target distribution. We thus conclude that these regularization techniques can improve the quality of the generator learned from empirical data for a large class of distributions.

Multi-class classification: mirror descent approach

We consider the problem of multi-class classification and a stochastic opti- mization approach to it. We derive risk bounds for stochastic mirror descent algorithm and provide examples of set geometries that make the use of the algorithm efficient in terms of error in k.

Tight Risk Bounds for Multi-Class Margin Classifiers

We consider a problem of risk estimation for large-margin multi-class classifiers. We propose a novel risk bound for the multi-class classification problem. The bound involves the marginal distribution of the classifier and the Rademacher complexity of the hypothesis class. We prove that our bound is tight in the number of classes. Finally, we compare our bound with the related ones and provide a simplified version of the bound for the multi-class classification with kernel based hypotheses.