Xiugang Wu
Understanding Entropic Regularization in GANs
Nov 02, 2021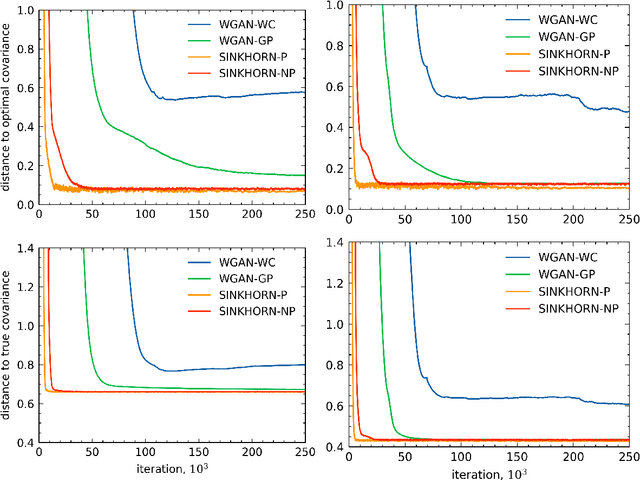
Abstract:Generative Adversarial Networks are a popular method for learning distributions from data by modeling the target distribution as a function of a known distribution. The function, often referred to as the generator, is optimized to minimize a chosen distance measure between the generated and target distributions. One commonly used measure for this purpose is the Wasserstein distance. However, Wasserstein distance is hard to compute and optimize, and in practice entropic regularization techniques are used to improve numerical convergence. The influence of regularization on the learned solution, however, remains not well-understood. In this paper, we study how several popular entropic regularizations of Wasserstein distance impact the solution in a simple benchmark setting where the generator is linear and the target distribution is high-dimensional Gaussian. We show that entropy regularization promotes the solution sparsification, while replacing the Wasserstein distance with the Sinkhorn divergence recovers the unregularized solution. Both regularization techniques remove the curse of dimensionality suffered by Wasserstein distance. We show that the optimal generator can be learned to accuracy $\epsilon$ with $O(1/\epsilon^2)$ samples from the target distribution. We thus conclude that these regularization techniques can improve the quality of the generator learned from empirical data for a large class of distributions.
Information Constrained Optimal Transport: From Talagrand, to Marton, to Cover
Aug 24, 2020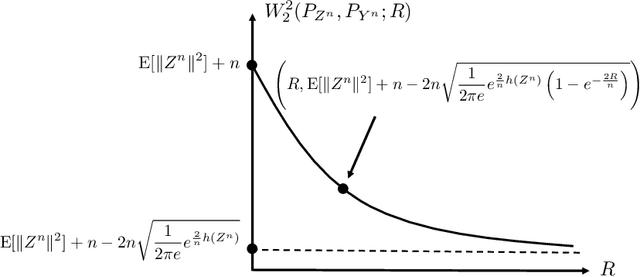
Abstract:The optimal transport problem studies how to transport one measure to another in the most cost-effective way and has wide range of applications from economics to machine learning. In this paper, we introduce and study an information constrained variation of this problem. Our study yields a strengthening and generalization of Talagrand's celebrated transportation cost inequality. Following Marton's approach, we show that the new transportation cost inequality can be used to recover old and new concentration of measure results. Finally, we provide an application of this new inequality to network information theory. We show that it can be used to recover almost immediately a recent solution to a long-standing open problem posed by Cover regarding the capacity of the relay channel.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge