Yikun Bai
Transport Based Mean Flows for Generative Modeling
Sep 26, 2025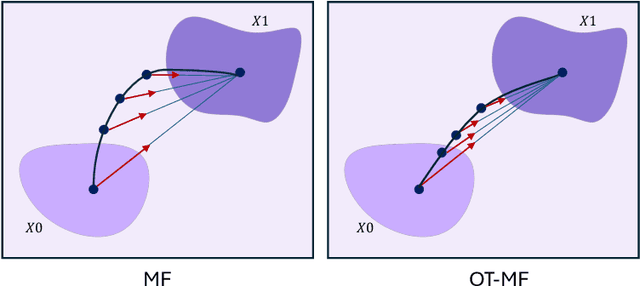


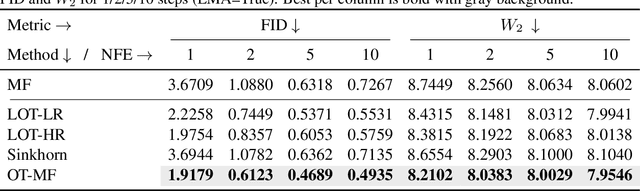
Abstract:Flow-matching generative models have emerged as a powerful paradigm for continuous data generation, achieving state-of-the-art results across domains such as images, 3D shapes, and point clouds. Despite their success, these models suffer from slow inference due to the requirement of numerous sequential sampling steps. Recent work has sought to accelerate inference by reducing the number of sampling steps. In particular, Mean Flows offer a one-step generation approach that delivers substantial speedups while retaining strong generative performance. Yet, in many continuous domains, Mean Flows fail to faithfully approximate the behavior of the original multi-step flow-matching process. In this work, we address this limitation by incorporating optimal transport-based sampling strategies into the Mean Flow framework, enabling one-step generators that better preserve the fidelity and diversity of the original multi-step flow process. Experiments on controlled low-dimensional settings and on high-dimensional tasks such as image generation, image-to-image translation, and point cloud generation demonstrate that our approach achieves superior inference accuracy in one-step generative modeling.
Understanding Learning with Sliced-Wasserstein Requires Rethinking Informative Slices
Nov 16, 2024Abstract:The practical applications of Wasserstein distances (WDs) are constrained by their sample and computational complexities. Sliced-Wasserstein distances (SWDs) provide a workaround by projecting distributions onto one-dimensional subspaces, leveraging the more efficient, closed-form WDs for one-dimensional distributions. However, in high dimensions, most random projections become uninformative due to the concentration of measure phenomenon. Although several SWD variants have been proposed to focus on \textit{informative} slices, they often introduce additional complexity, numerical instability, and compromise desirable theoretical (metric) properties of SWD. Amidst the growing literature that focuses on directly modifying the slicing distribution, which often face challenges, we revisit the classical Sliced-Wasserstein and propose instead to rescale the 1D Wasserstein to make all slices equally informative. Importantly, we show that with an appropriate data assumption and notion of \textit{slice informativeness}, rescaling for all individual slices simplifies to \textbf{a single global scaling factor} on the SWD. This, in turn, translates to the standard learning rate search for gradient-based learning in common machine learning workflows. We perform extensive experiments across various machine learning tasks showing that the classical SWD, when properly configured, can often match or surpass the performance of more complex variants. We then answer the following question: "Is Sliced-Wasserstein all you need for common learning tasks?"
Linear Spherical Sliced Optimal Transport: A Fast Metric for Comparing Spherical Data
Nov 09, 2024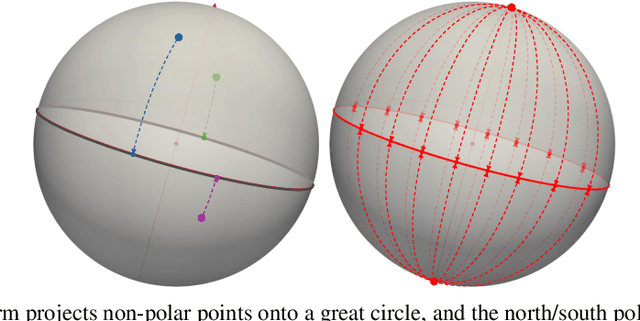
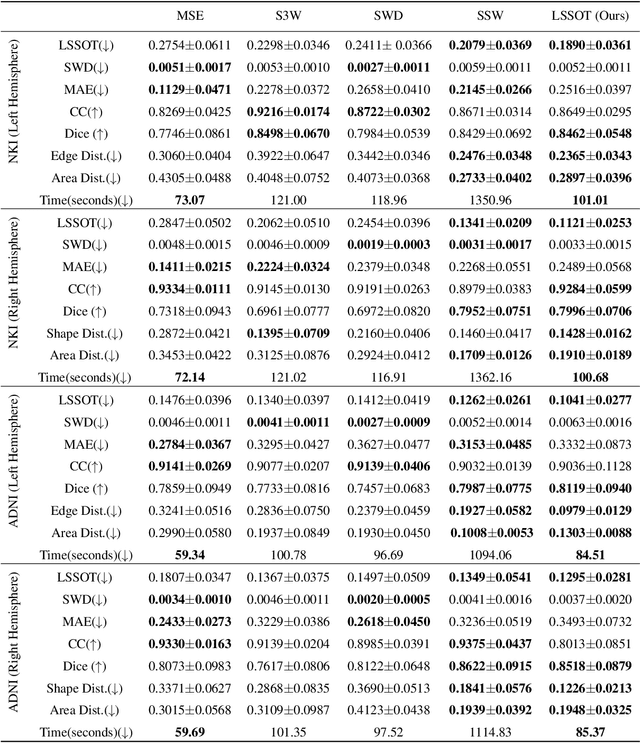
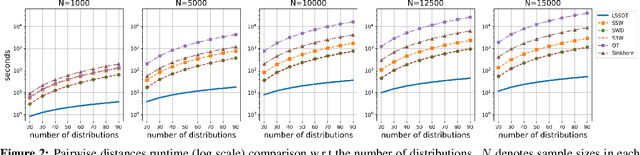
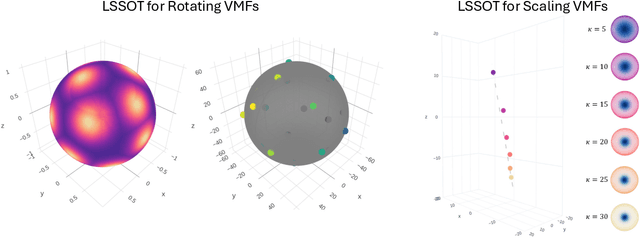
Abstract:Efficient comparison of spherical probability distributions becomes important in fields such as computer vision, geosciences, and medicine. Sliced optimal transport distances, such as spherical and stereographic spherical sliced Wasserstein distances, have recently been developed to address this need. These methods reduce the computational burden of optimal transport by slicing hyperspheres into one-dimensional projections, i.e., lines or circles. Concurrently, linear optimal transport has been proposed to embed distributions into \( L^2 \) spaces, where the \( L^2 \) distance approximates the optimal transport distance, thereby simplifying comparisons across multiple distributions. In this work, we introduce the Linear Spherical Sliced Optimal Transport (LSSOT) framework, which utilizes slicing to embed spherical distributions into \( L^2 \) spaces while preserving their intrinsic geometry, offering a computationally efficient metric for spherical probability measures. We establish the metricity of LSSOT and demonstrate its superior computational efficiency in applications such as cortical surface registration, 3D point cloud interpolation via gradient flow, and shape embedding. Our results demonstrate the significant computational benefits and high accuracy of LSSOT in these applications.
Linear Partial Gromov-Wasserstein Embedding
Oct 22, 2024



Abstract:The Gromov Wasserstein (GW) problem, a variant of the classical optimal transport (OT) problem, has attracted growing interest in the machine learning and data science communities due to its ability to quantify similarity between measures in different metric spaces. However, like the classical OT problem, GW imposes an equal mass constraint between measures, which restricts its application in many machine learning tasks. To address this limitation, the partial Gromov-Wasserstein (PGW) problem has been introduced, which relaxes the equal mass constraint, enabling the comparison of general positive Radon measures. Despite this, both GW and PGW face significant computational challenges due to their non-convex nature. To overcome these challenges, we propose the linear partial Gromov-Wasserstein (LPGW) embedding, a linearized embedding technique for the PGW problem. For $K$ different metric measure spaces, the pairwise computation of the PGW distance requires solving the PGW problem $\mathcal{O}(K^2)$ times. In contrast, the proposed linearization technique reduces this to $\mathcal{O}(K)$ times. Similar to the linearization technique for the classical OT problem, we prove that LPGW defines a valid metric for metric measure spaces. Finally, we demonstrate the effectiveness of LPGW in practical applications such as shape retrieval and learning with transport-based embeddings, showing that LPGW preserves the advantages of PGW in partial matching while significantly enhancing computational efficiency.
Expected Sliced Transport Plans
Oct 17, 2024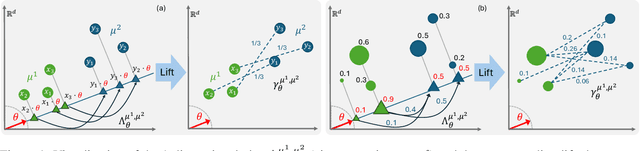
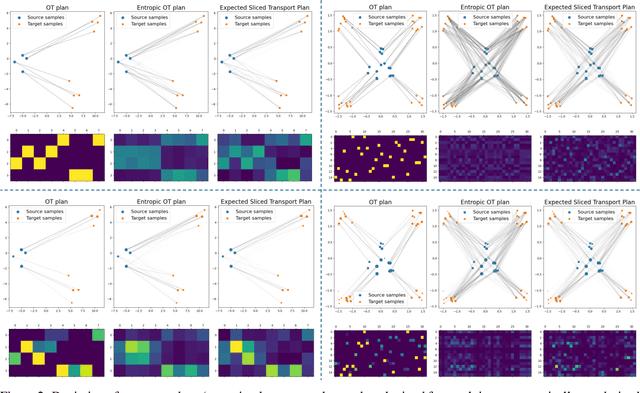
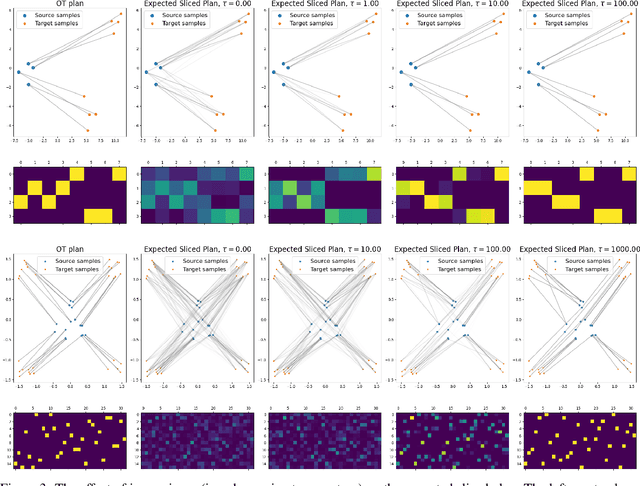

Abstract:The optimal transport (OT) problem has gained significant traction in modern machine learning for its ability to: (1) provide versatile metrics, such as Wasserstein distances and their variants, and (2) determine optimal couplings between probability measures. To reduce the computational complexity of OT solvers, methods like entropic regularization and sliced optimal transport have been proposed. The sliced OT framework improves efficiency by comparing one-dimensional projections (slices) of high-dimensional distributions. However, despite their computational efficiency, sliced-Wasserstein approaches lack a transportation plan between the input measures, limiting their use in scenarios requiring explicit coupling. In this paper, we address two key questions: Can a transportation plan be constructed between two probability measures using the sliced transport framework? If so, can this plan be used to define a metric between the measures? We propose a "lifting" operation to extend one-dimensional optimal transport plans back to the original space of the measures. By computing the expectation of these lifted plans, we derive a new transportation plan, termed expected sliced transport (EST) plans. We prove that using the EST plan to weight the sum of the individual Euclidean costs for moving from one point to another results in a valid metric between the input discrete probability measures. We demonstrate the connection between our approach and the recently proposed min-SWGG, along with illustrative numerical examples that support our theoretical findings.
Sinkhorn algorithms and linear programming solvers for optimal partial transport problems
Jul 09, 2024Abstract:In this note, we generalize the classical optimal partial transport (OPT) problem by modifying the mass destruction/creation term to function-based terms, introducing what we term ``generalized optimal partial transport'' problems. We then discuss the dual formulation of these problems and the associated Sinkhorn solver. Finally, we explore how these new OPT problems relate to classical optimal transport (OT) problems and introduce a linear programming solver tailored for these generalized scenarios.
Efficient Solvers for Partial Gromov-Wasserstein
Feb 06, 2024



Abstract:The partial Gromov-Wasserstein (PGW) problem facilitates the comparison of measures with unequal masses residing in potentially distinct metric spaces, thereby enabling unbalanced and partial matching across these spaces. In this paper, we demonstrate that the PGW problem can be transformed into a variant of the Gromov-Wasserstein problem, akin to the conversion of the partial optimal transport problem into an optimal transport problem. This transformation leads to two new solvers, mathematically and computationally equivalent, based on the Frank-Wolfe algorithm, that provide efficient solutions to the PGW problem. We further establish that the PGW problem constitutes a metric for metric measure spaces. Finally, we validate the effectiveness of our proposed solvers in terms of computation time and performance on shape-matching and positive-unlabeled learning problems, comparing them against existing baselines.
Stereographic Spherical Sliced Wasserstein Distances
Feb 04, 2024



Abstract:Comparing spherical probability distributions is of great interest in various fields, including geology, medical domains, computer vision, and deep representation learning. The utility of optimal transport-based distances, such as the Wasserstein distance, for comparing probability measures has spurred active research in developing computationally efficient variations of these distances for spherical probability measures. This paper introduces a high-speed and highly parallelizable distance for comparing spherical measures using the stereographic projection and the generalized Radon transform, which we refer to as the Stereographic Spherical Sliced Wasserstein (S3W) distance. We carefully address the distance distortion caused by the stereographic projection and provide an extensive theoretical analysis of our proposed metric and its rotationally invariant variation. Finally, we evaluate the performance of the proposed metrics and compare them with recent baselines in terms of both speed and accuracy through a wide range of numerical studies, including gradient flows and self-supervised learning.
LCOT: Linear circular optimal transport
Oct 09, 2023



Abstract:The optimal transport problem for measures supported on non-Euclidean spaces has recently gained ample interest in diverse applications involving representation learning. In this paper, we focus on circular probability measures, i.e., probability measures supported on the unit circle, and introduce a new computationally efficient metric for these measures, denoted as Linear Circular Optimal Transport (LCOT). The proposed metric comes with an explicit linear embedding that allows one to apply Machine Learning (ML) algorithms to the embedded measures and seamlessly modify the underlying metric for the ML algorithm to LCOT. We show that the proposed metric is rooted in the Circular Optimal Transport (COT) and can be considered the linearization of the COT metric with respect to a fixed reference measure. We provide a theoretical analysis of the proposed metric and derive the computational complexities for pairwise comparison of circular probability measures. Lastly, through a set of numerical experiments, we demonstrate the benefits of LCOT in learning representations of circular measures.
Partial Transport for Point-Cloud Registration
Sep 27, 2023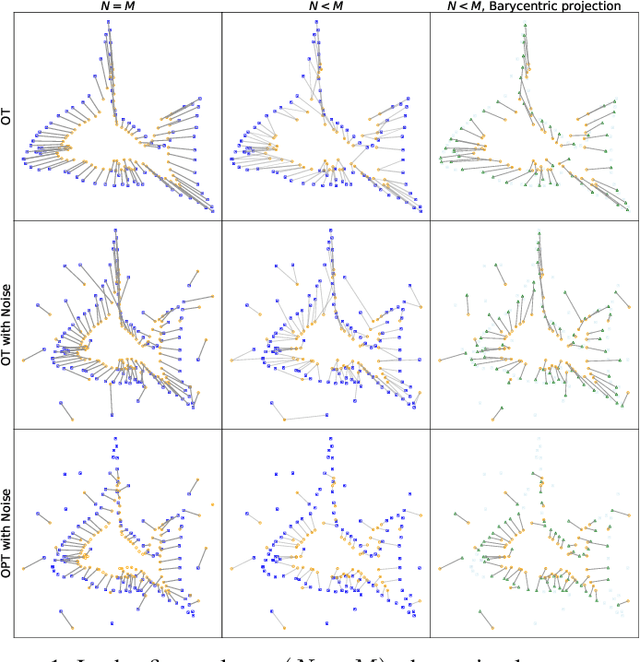
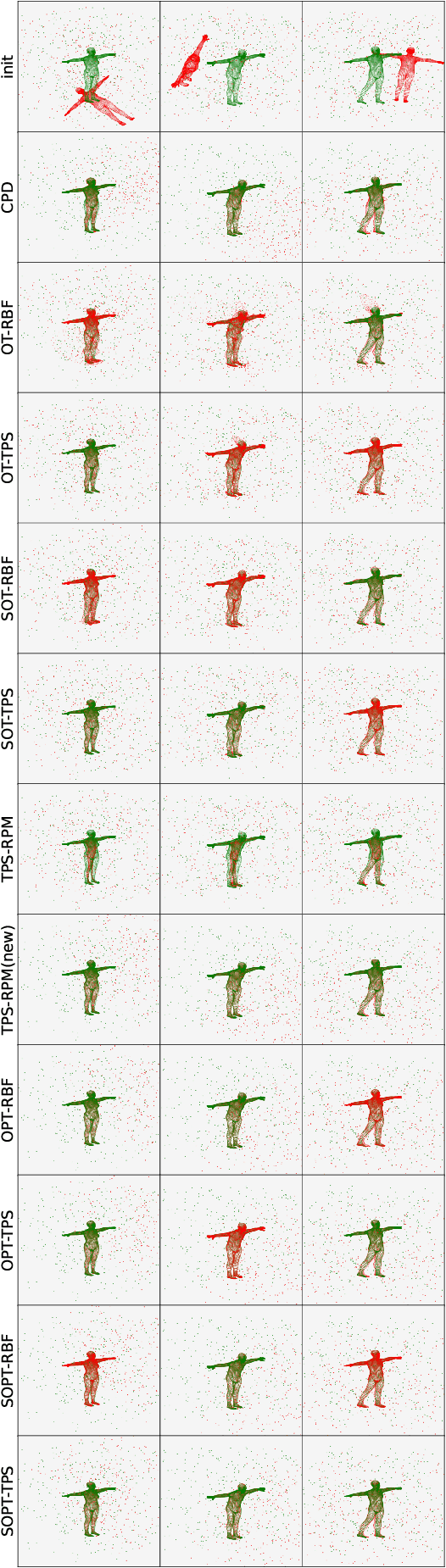
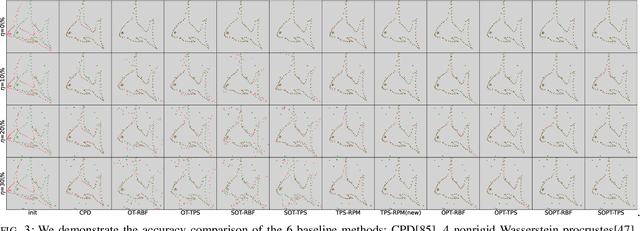
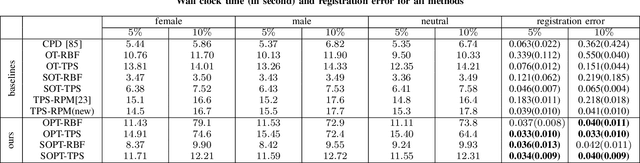
Abstract:Point cloud registration plays a crucial role in various fields, including robotics, computer graphics, and medical imaging. This process involves determining spatial relationships between different sets of points, typically within a 3D space. In real-world scenarios, complexities arise from non-rigid movements and partial visibility, such as occlusions or sensor noise, making non-rigid registration a challenging problem. Classic non-rigid registration methods are often computationally demanding, suffer from unstable performance, and, importantly, have limited theoretical guarantees. The optimal transport problem and its unbalanced variations (e.g., the optimal partial transport problem) have emerged as powerful tools for point-cloud registration, establishing a strong benchmark in this field. These methods view point clouds as empirical measures and provide a mathematically rigorous way to quantify the `correspondence' between (the transformed) source and target points. In this paper, we approach the point-cloud registration problem through the lens of optimal transport theory and first propose a comprehensive set of non-rigid registration methods based on the optimal partial transportation problem. Subsequently, leveraging the emerging work on efficient solutions to the one-dimensional optimal partial transport problem, we extend our proposed algorithms via slicing to gain significant computational efficiency, resulting in fast and robust non-rigid registration algorithms. We demonstrate the effectiveness of our proposed methods and compare them against baselines on various 3D and 2D non-rigid registration problems where the source and target point clouds are corrupted by random noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge