Partial Transport for Point-Cloud Registration
Paper and Code
Sep 27, 2023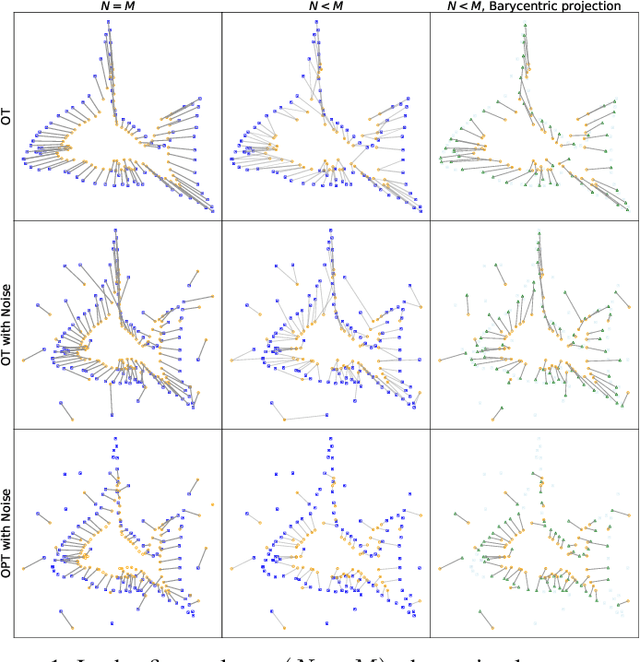
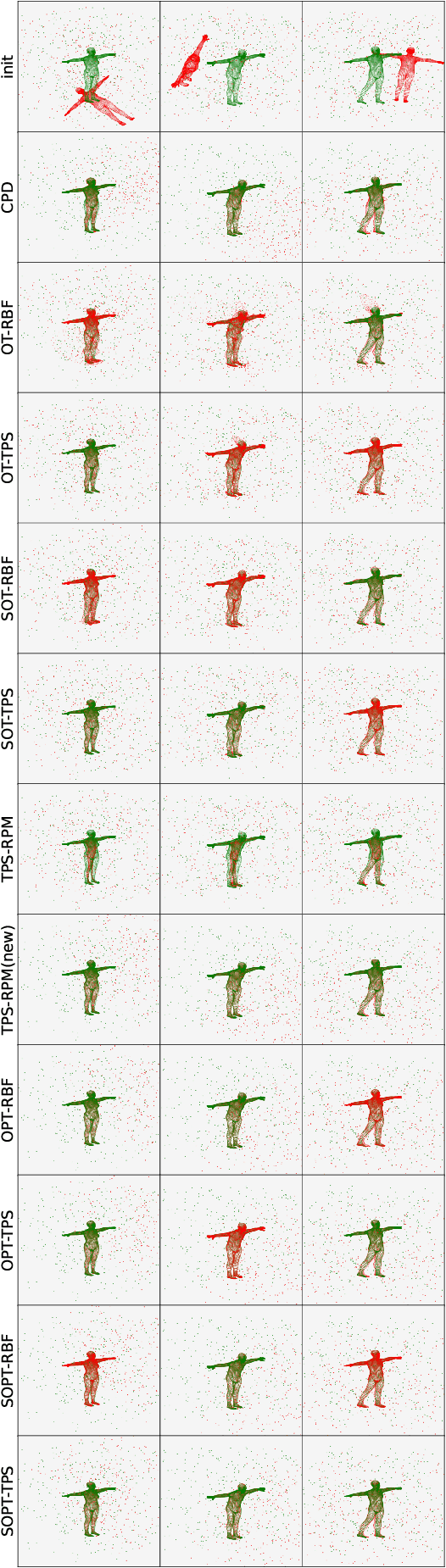
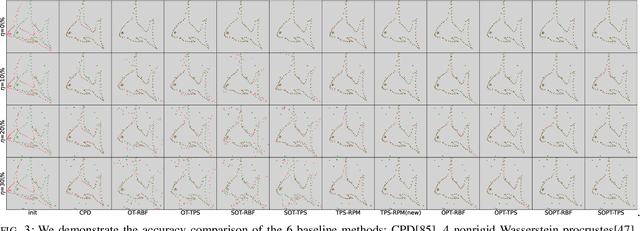
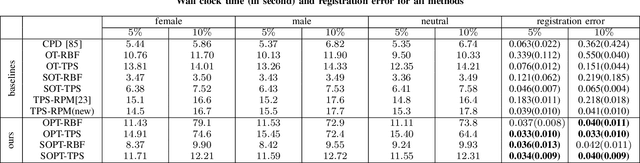
Point cloud registration plays a crucial role in various fields, including robotics, computer graphics, and medical imaging. This process involves determining spatial relationships between different sets of points, typically within a 3D space. In real-world scenarios, complexities arise from non-rigid movements and partial visibility, such as occlusions or sensor noise, making non-rigid registration a challenging problem. Classic non-rigid registration methods are often computationally demanding, suffer from unstable performance, and, importantly, have limited theoretical guarantees. The optimal transport problem and its unbalanced variations (e.g., the optimal partial transport problem) have emerged as powerful tools for point-cloud registration, establishing a strong benchmark in this field. These methods view point clouds as empirical measures and provide a mathematically rigorous way to quantify the `correspondence' between (the transformed) source and target points. In this paper, we approach the point-cloud registration problem through the lens of optimal transport theory and first propose a comprehensive set of non-rigid registration methods based on the optimal partial transportation problem. Subsequently, leveraging the emerging work on efficient solutions to the one-dimensional optimal partial transport problem, we extend our proposed algorithms via slicing to gain significant computational efficiency, resulting in fast and robust non-rigid registration algorithms. We demonstrate the effectiveness of our proposed methods and compare them against baselines on various 3D and 2D non-rigid registration problems where the source and target point clouds are corrupted by random noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge