Steven B. Damelin
On Uniform Weighted Deep Polynomial approximation
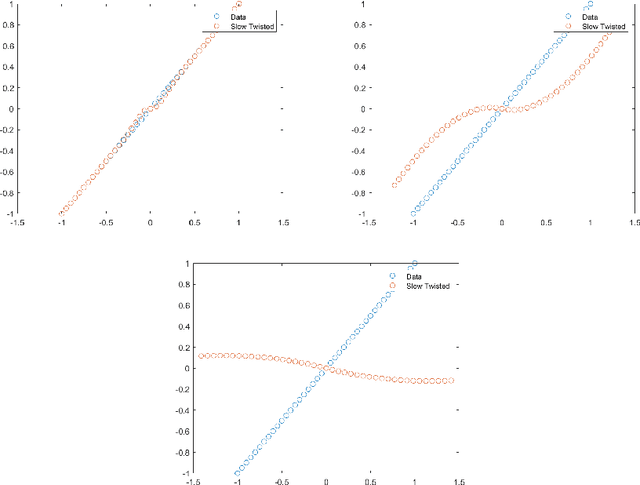
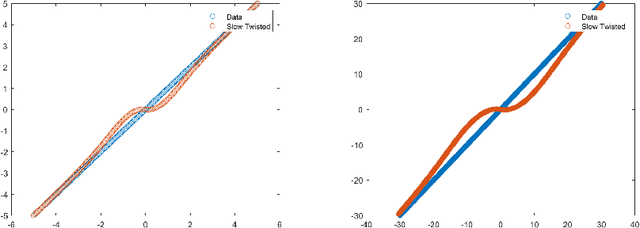
Jun 26, 2025Abstract:It is a classical result in rational approximation theory that certain non-smooth or singular functions, such as $|x|$ and $x^{1/p}$, can be efficiently approximated using rational functions with root-exponential convergence in terms of degrees of freedom \cite{Sta, GN}. In contrast, polynomial approximations admit only algebraic convergence by Jackson's theorem \cite{Lub2}. Recent work shows that composite polynomial architectures can recover exponential approximation rates even without smoothness \cite{KY}. In this work, we introduce and analyze a class of weighted deep polynomial approximants tailored for functions with asymmetric behavior-growing unbounded on one side and decaying on the other. By multiplying a learnable deep polynomial with a one-sided weight, we capture both local non-smoothness and global growth. We show numerically that this framework outperforms Taylor, Chebyshev, and standard deep polynomial approximants, even when all use the same number of parameters. To optimize these approximants in practice, we propose a stable graph-based parameterization strategy building on \cite{Jar}.
Partial Transport for Point-Cloud Registration
Sep 27, 2023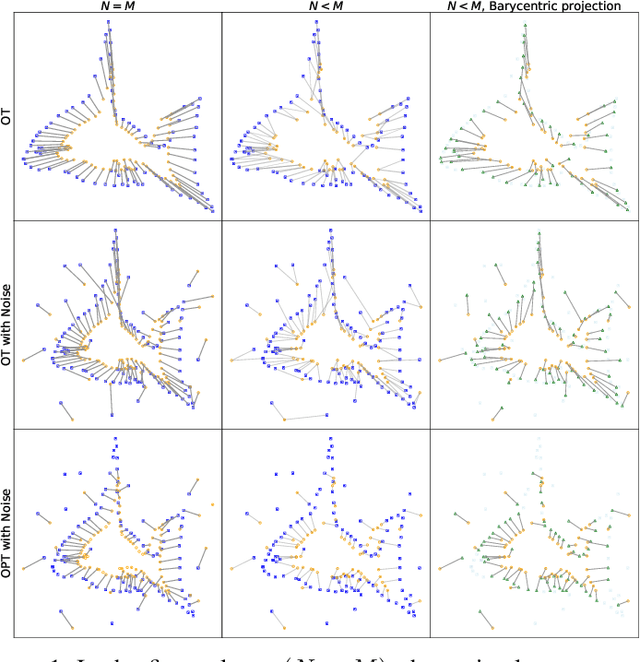
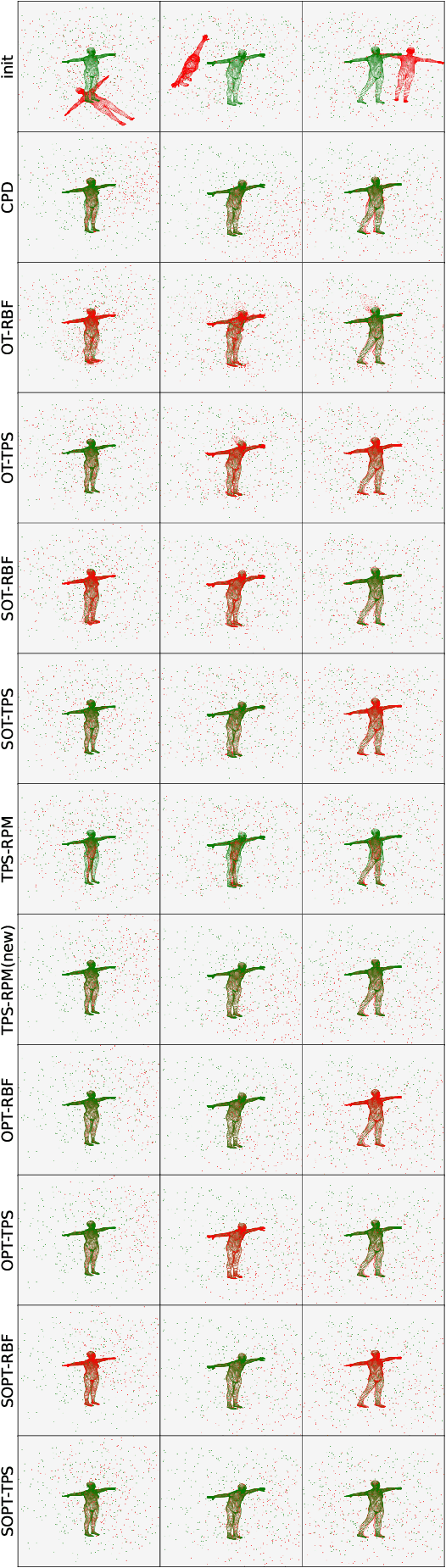
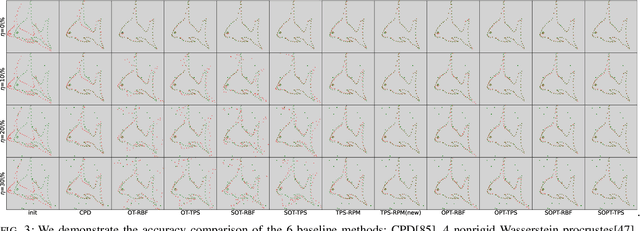
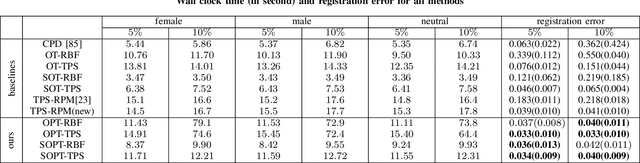
Abstract:Point cloud registration plays a crucial role in various fields, including robotics, computer graphics, and medical imaging. This process involves determining spatial relationships between different sets of points, typically within a 3D space. In real-world scenarios, complexities arise from non-rigid movements and partial visibility, such as occlusions or sensor noise, making non-rigid registration a challenging problem. Classic non-rigid registration methods are often computationally demanding, suffer from unstable performance, and, importantly, have limited theoretical guarantees. The optimal transport problem and its unbalanced variations (e.g., the optimal partial transport problem) have emerged as powerful tools for point-cloud registration, establishing a strong benchmark in this field. These methods view point clouds as empirical measures and provide a mathematically rigorous way to quantify the `correspondence' between (the transformed) source and target points. In this paper, we approach the point-cloud registration problem through the lens of optimal transport theory and first propose a comprehensive set of non-rigid registration methods based on the optimal partial transportation problem. Subsequently, leveraging the emerging work on efficient solutions to the one-dimensional optimal partial transport problem, we extend our proposed algorithms via slicing to gain significant computational efficiency, resulting in fast and robust non-rigid registration algorithms. We demonstrate the effectiveness of our proposed methods and compare them against baselines on various 3D and 2D non-rigid registration problems where the source and target point clouds are corrupted by random noise.
A Multiple Parameter Linear Scale-Space for one dimensional Signal Classification
May 22, 2023Abstract:In this article we construct a maximal set of kernels for a multi-parameter linear scale-space that allow us to construct trees for classification and recognition of one-dimensional continuous signals similar the Gaussian linear scale-space approach. Fourier transform formulas are provided and used for quick and efficient computations. A number of useful properties of the maximal set of kernels are derived. We also strengthen and generalize some previous results on the classification of Gaussian kernels. Finally, a new topologically invariant method of constructing trees is introduced.
On a realization of motion and similarity group equivalence classes of labeled points in $\mathbb R^k$ with applications to computer vision
Mar 24, 2021Abstract:We study a realization of motion and similarity group equivalence classes of $n\geq 1$ labeled points in $\mathbb R^k,\, k\geq 1$ as a metric space with a computable metric. Our study is motivated by applications in computer vision.
Well Separated Pair Decomposition and power weighted shortest path metric algorithm fusion
Mar 20, 2021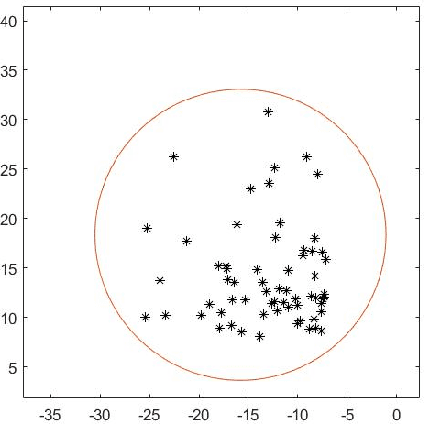
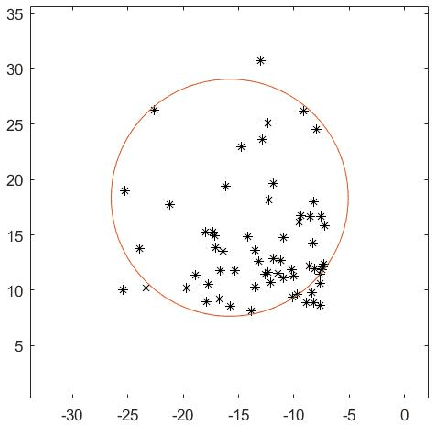
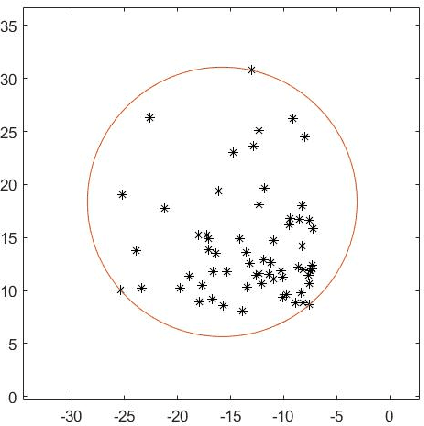
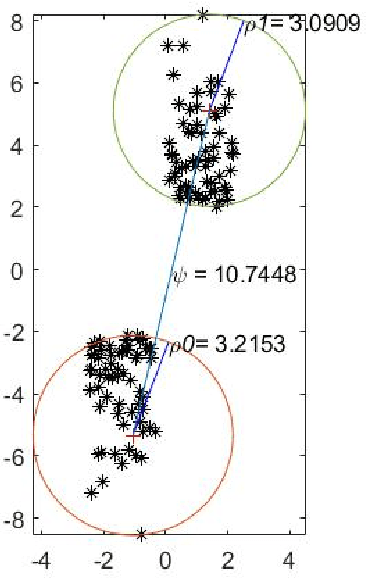
Abstract:For $s$ $>$ 0, we consider an algorithm that computes all $s$-well separated pairs in certain point sets in $\mathbb{R}^{n}$, $n$ $>1$. For an integer $K$ $>1$, we also consider an algorithm that is a permutation of Dijkstra's algorithm, that computes $K$-nearest neighbors using a certain power weighted shortest path metric in $\mathbb{R}^{n}$, $n$ $>$ $1$. We describe each algorithm and their respective dependencies on the input data. We introduce a way to combine both algorithms into a fused algorithm. Several open problems are given for future research.
On the Whitney extension problem for near isometries and beyond
Mar 17, 2021

Abstract:This paper is an exposition of work of the author et al. detailing fascinating connections between several mathematical problems which lie on the intersection of several mathematics subjects, namely algebraic-differential geometry, analysis on manifolds, complex-harmonic analysis, data science, partial differential equations, optimization and probability. A significant portion of the work is based on joint research with Charles Fefferman in the papers [39, 40, 41, 42]. The topics of this work include (a) The space of maps of bounded mean oscillation (BMO) in $\mathbb R^D,\, D\geq 2$. (b) The labeled and unlabeled near alignment and Procrustes problem for point sets with certain geometries and for not too thin compact sets both in $\mathbb R^D,\, D\geq 2$. (c) The Whitney near isometry extension problem for point sets with certain geometries and for not too thin compact sets both in $\mathbb R^D,\, D\geq 2$. (d) Partitions and clustering of compact sets and point sets with certain geometries in $\mathbb R^D,\, D\geq 2$ and analysis on certain manifolds in $\mathbb R^D,\, D\geq 2$. Many open problems for future research are given.
Classification Constrained Dimensionality Reduction
Feb 21, 2008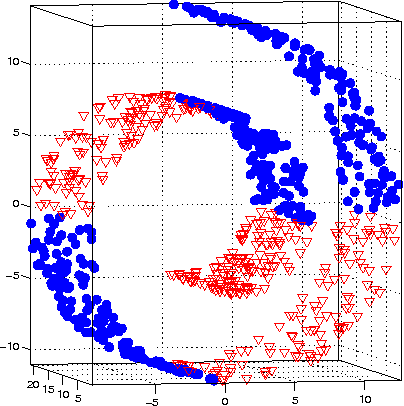
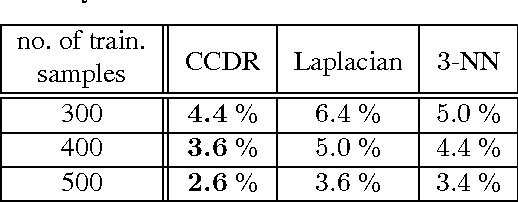
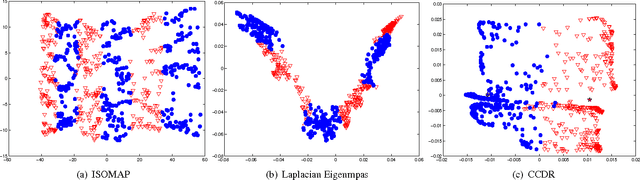
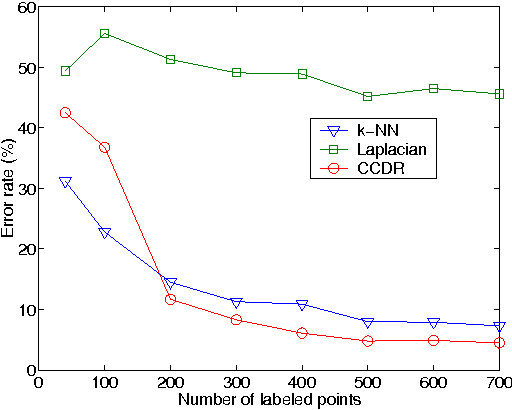
Abstract:Dimensionality reduction is a topic of recent interest. In this paper, we present the classification constrained dimensionality reduction (CCDR) algorithm to account for label information. The algorithm can account for multiple classes as well as the semi-supervised setting. We present an out-of-sample expressions for both labeled and unlabeled data. For unlabeled data, we introduce a method of embedding a new point as preprocessing to a classifier. For labeled data, we introduce a method that improves the embedding during the training phase using the out-of-sample extension. We investigate classification performance using the CCDR algorithm on hyper-spectral satellite imagery data. We demonstrate the performance gain for both local and global classifiers and demonstrate a 10% improvement of the $k$-nearest neighbors algorithm performance. We present a connection between intrinsic dimension estimation and the optimal embedding dimension obtained using the CCDR algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge