Well Separated Pair Decomposition and power weighted shortest path metric algorithm fusion
Paper and Code
Mar 20, 2021
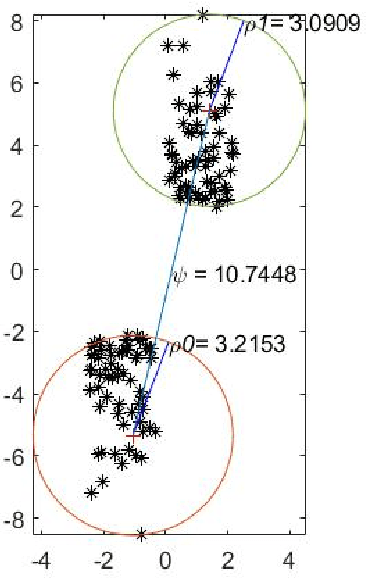
For $s$ $>$ 0, we consider an algorithm that computes all $s$-well separated pairs in certain point sets in $\mathbb{R}^{n}$, $n$ $>1$. For an integer $K$ $>1$, we also consider an algorithm that is a permutation of Dijkstra's algorithm, that computes $K$-nearest neighbors using a certain power weighted shortest path metric in $\mathbb{R}^{n}$, $n$ $>$ $1$. We describe each algorithm and their respective dependencies on the input data. We introduce a way to combine both algorithms into a fused algorithm. Several open problems are given for future research.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge