ApHMM: Accelerating Profile Hidden Markov Models for Fast and Energy-Efficient Genome Analysis

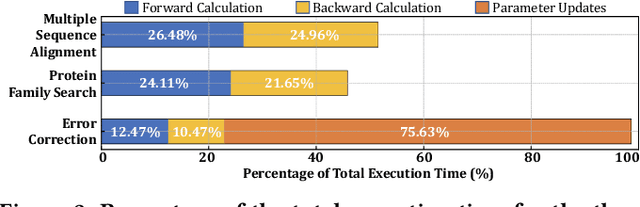
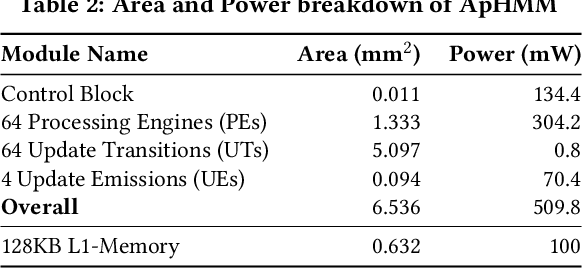
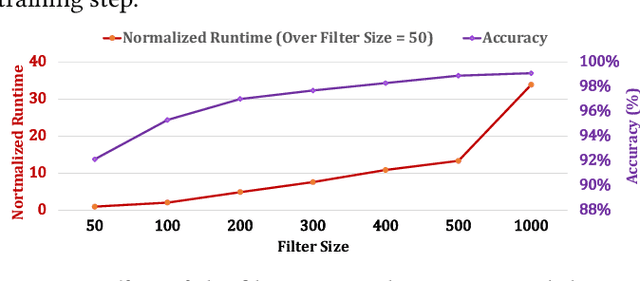
Profile hidden Markov models (pHMMs) are widely used in many bioinformatics applications to accurately identify similarities between biological sequences (e.g., DNA or protein sequences). PHMMs use a commonly-adopted and highly-accurate method, called the Baum-Welch algorithm, to calculate these similarities. However, the Baum-Welch algorithm is computationally expensive, and existing works provide either software- or hardware-only solutions for a fixed pHMM design. When we analyze the state-of-the-art works, we find that there is a pressing need for a flexible, high-performant, and energy-efficient hardware-software co-design to efficiently and effectively solve all the major inefficiencies in the Baum-Welch algorithm for pHMMs. We propose ApHMM, the first flexible acceleration framework that can significantly reduce computational and energy overheads of the Baum-Welch algorithm for pHMMs. ApHMM leverages hardware-software co-design to solve the major inefficiencies in the Baum-Welch algorithm by 1) designing a flexible hardware to support different pHMMs designs, 2) exploiting the predictable data dependency pattern in an on-chip memory with memoization techniques, 3) quickly eliminating negligible computations with a hardware-based filter, and 4) minimizing the redundant computations. We implement our 1) hardware-software optimizations on a specialized hardware and 2) software optimizations for GPUs to provide the first flexible Baum-Welch accelerator for pHMMs. ApHMM provides significant speedups of 15.55x-260.03x, 1.83x-5.34x, and 27.97x compared to CPU, GPU, and FPGA implementations of the Baum-Welch algorithm, respectively. ApHMM outperforms the state-of-the-art CPU implementations of three important bioinformatics applications, 1) error correction, 2) protein family search, and 3) multiple sequence alignment, by 1.29x-59.94x, 1.03x-1.75x, and 1.03x-1.95x, respectively.

Well Separated Pair Decomposition and power weighted shortest path metric algorithm fusion

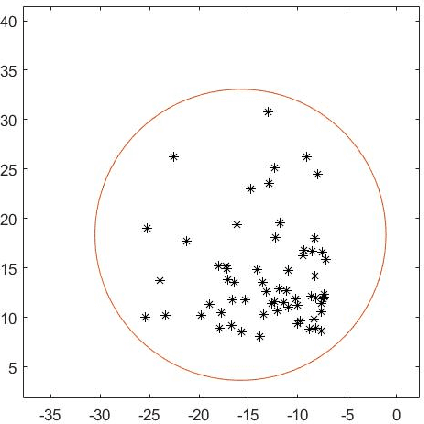
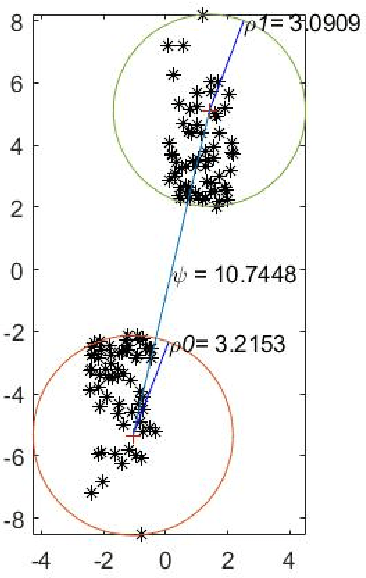
For $s$ $>$ 0, we consider an algorithm that computes all $s$-well separated pairs in certain point sets in $\mathbb{R}^{n}$, $n$ $>1$. For an integer $K$ $>1$, we also consider an algorithm that is a permutation of Dijkstra's algorithm, that computes $K$-nearest neighbors using a certain power weighted shortest path metric in $\mathbb{R}^{n}$, $n$ $>$ $1$. We describe each algorithm and their respective dependencies on the input data. We introduce a way to combine both algorithms into a fused algorithm. Several open problems are given for future research.