Soheil Kolouri
Zero Sum SVD: Balancing Loss Sensitivity for Low Rank LLM Compression
Feb 02, 2026Abstract:Advances in large language models have driven strong performance across many tasks, but their memory and compute costs still hinder deployment. SVD-based compression reduces storage and can speed up inference via low-rank factors, yet performance depends on how rank is allocated under a global compression ratio. Prior methods often use homogeneous ranks for similarly sized matrices, despite large differences in loss sensitivity, or rely on expensive iterative pre-truncation optimization to determine per matrix ranks. We propose \textbf{Zero Sum SVD} (\textbf{ZS-SVD}), a post-training method that performs \emph{global} singular component selection using activation whitening and first-order calibration loss estimates in whitened coordinates. \textbf{ZS-SVD} prunes components across the whole model with a \textbf{zero sum} rule that keeps the cumulative predicted loss change near zero, automatically yielding heterogeneous ranks without solving a rank allocation optimization. Motivated by evidence that gradients near pretrained solutions exhibit low rank structure, we also introduce an optional lightweight correction that applies a \textbf{single} projected gradient update after truncation, followed by re-truncation. Extensive experiments across multiple LLM architectures show consistent gains across diverse benchmarks and compression ratios. Code is available at https://github.com/mint-vu/Zero-Sum-SVD
LUNA: Linear Universal Neural Attention with Generalization Guarantees
Dec 08, 2025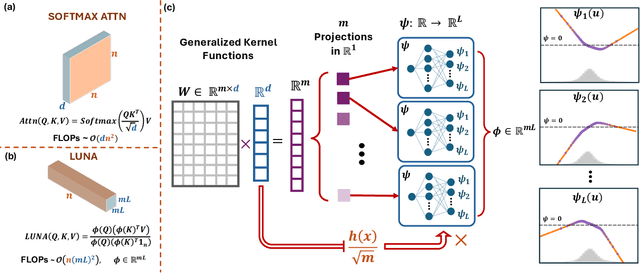
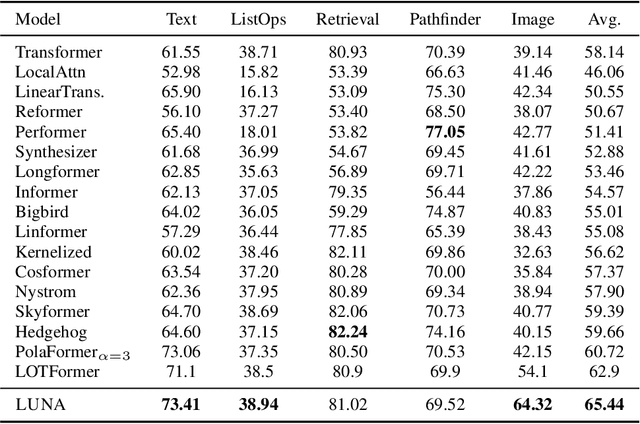
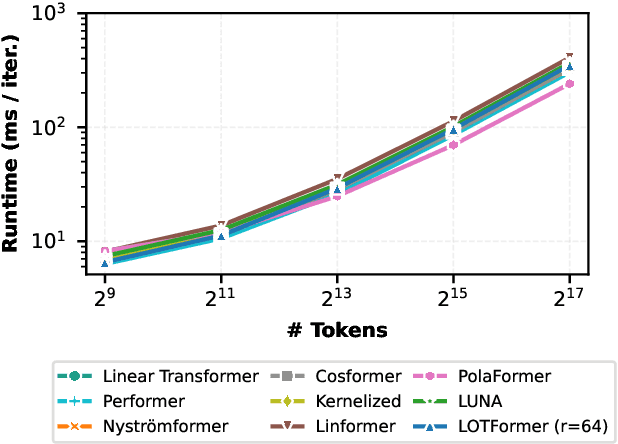
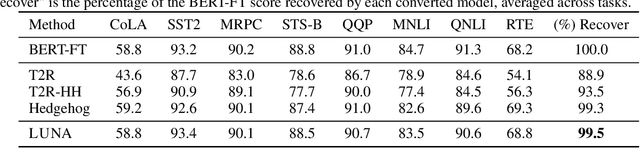
Abstract:Scaling attention faces a critical bottleneck: the $\mathcal{O}(n^2)$ quadratic computational cost of softmax attention, which limits its application in long-sequence domains. While linear attention mechanisms reduce this cost to $\mathcal{O}(n)$, they typically rely on fixed random feature maps, such as random Fourier features or hand-crafted functions. This reliance on static, data-agnostic kernels creates a fundamental trade-off, forcing practitioners to sacrifice significant model accuracy for computational efficiency. We introduce \textsc{LUNA}, a kernelized linear attention mechanism that eliminates this trade-off, retaining linear cost while matching and surpassing the accuracy of quadratic attention. \textsc{LUNA} is built on the key insight that the kernel feature map itself should be learned rather than fixed a priori. By parameterizing the kernel, \textsc{LUNA} learns a feature basis tailored to the specific data and task, overcoming the expressive limitations of fixed-feature methods. \textsc{Luna} implements this with a learnable feature map that induces a positive-definite kernel and admits a streaming form, yielding linear time and memory scaling in the sequence length. Empirical evaluations validate our approach across diverse settings. On the Long Range Arena (LRA), \textsc{Luna} achieves state-of-the-art average accuracy among efficient Transformers under compute parity, using the same parameter count, training steps, and approximate FLOPs. \textsc{Luna} also excels at post-hoc conversion: replacing softmax in fine-tuned BERT and ViT-B/16 checkpoints and briefly fine-tuning recovers most of the original performance, substantially outperforming fixed linearizations.
Transport Based Mean Flows for Generative Modeling
Sep 26, 2025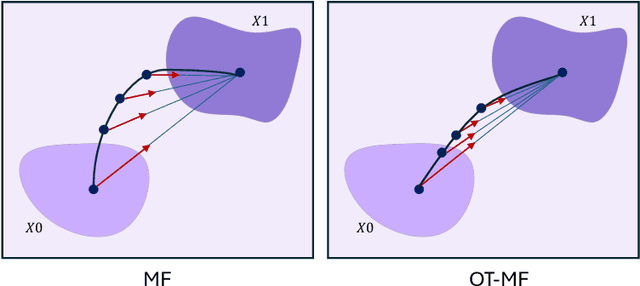


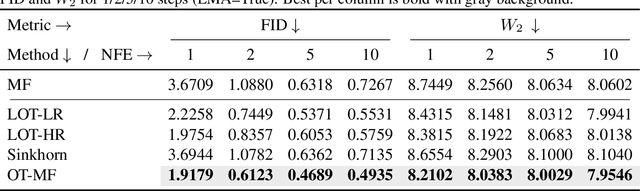
Abstract:Flow-matching generative models have emerged as a powerful paradigm for continuous data generation, achieving state-of-the-art results across domains such as images, 3D shapes, and point clouds. Despite their success, these models suffer from slow inference due to the requirement of numerous sequential sampling steps. Recent work has sought to accelerate inference by reducing the number of sampling steps. In particular, Mean Flows offer a one-step generation approach that delivers substantial speedups while retaining strong generative performance. Yet, in many continuous domains, Mean Flows fail to faithfully approximate the behavior of the original multi-step flow-matching process. In this work, we address this limitation by incorporating optimal transport-based sampling strategies into the Mean Flow framework, enabling one-step generators that better preserve the fidelity and diversity of the original multi-step flow process. Experiments on controlled low-dimensional settings and on high-dimensional tasks such as image generation, image-to-image translation, and point cloud generation demonstrate that our approach achieves superior inference accuracy in one-step generative modeling.
Neural-Augmented Kelvinlet: Real-Time Soft Tissue Deformation with Multiple Graspers
Jun 06, 2025Abstract:Fast and accurate simulation of soft tissue deformation is a critical factor for surgical robotics and medical training. In this paper, we introduce a novel physics-informed neural simulator that approximates soft tissue deformations in a realistic and real-time manner. Our framework integrates Kelvinlet-based priors into neural simulators, making it the first approach to leverage Kelvinlets for residual learning and regularization in data-driven soft tissue modeling. By incorporating large-scale Finite Element Method (FEM) simulations of both linear and nonlinear soft tissue responses, our method improves neural network predictions across diverse architectures, enhancing accuracy and physical consistency while maintaining low latency for real-time performance. We demonstrate the effectiveness of our approach by performing accurate surgical maneuvers that simulate the use of standard laparoscopic tissue grasping tools with high fidelity. These results establish Kelvinlet-augmented learning as a powerful and efficient strategy for real-time, physics-aware soft tissue simulation in surgical applications.
Collaborative Learning in Agentic Systems: A Collective AI is Greater Than the Sum of Its Parts
Jun 05, 2025Abstract:Agentic AI has gained significant interest as a research paradigm focused on autonomy, self-directed learning, and long-term reliability of decision making. Real-world agentic systems operate in decentralized settings on a large set of tasks or data distributions with constraints such as limited bandwidth, asynchronous execution, and the absence of a centralized model or even common objectives. We posit that exploiting previously learned skills, task similarities, and communication capabilities in a collective of agentic AI are challenging but essential elements to enabling scalability, open-endedness, and beneficial collaborative learning dynamics. In this paper, we introduce Modular Sharing and Composition in Collective Learning (MOSAIC), an agentic algorithm that allows multiple agents to independently solve different tasks while also identifying, sharing, and reusing useful machine-learned knowledge, without coordination, synchronization, or centralized control. MOSAIC combines three mechanisms: (1) modular policy composition via neural network masks, (2) cosine similarity estimation using Wasserstein embeddings for knowledge selection, and (3) asynchronous communication and policy integration. Results on a set of RL benchmarks show that MOSAIC has a greater sample efficiency than isolated learners, i.e., it learns significantly faster, and in some cases, finds solutions to tasks that cannot be solved by isolated learners. The collaborative learning and sharing dynamics are also observed to result in the emergence of ideal curricula of tasks, from easy to hard. These findings support the case for collaborative learning in agentic systems to achieve better and continuously evolving performance both at the individual and collective levels.
Knowledge Distillation and Dataset Distillation of Large Language Models: Emerging Trends, Challenges, and Future Directions
Apr 20, 2025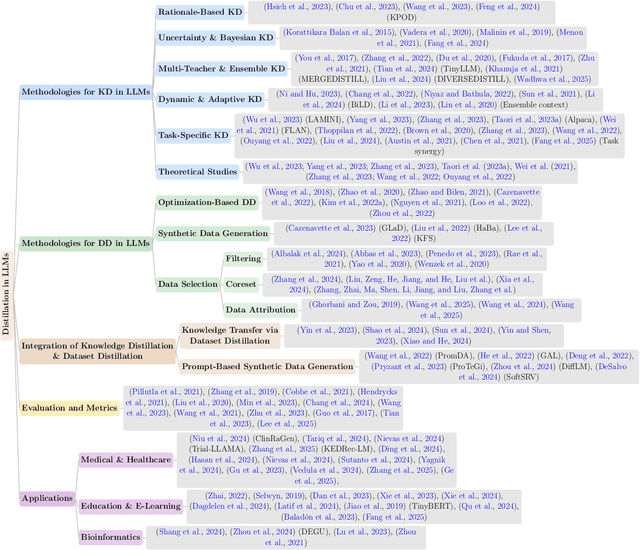
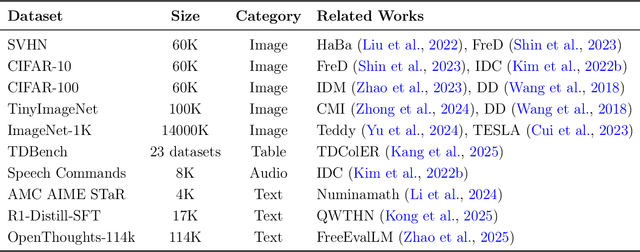
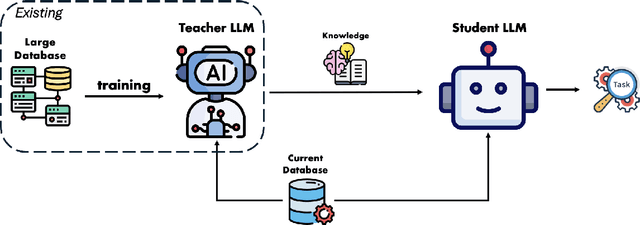

Abstract:The exponential growth of Large Language Models (LLMs) continues to highlight the need for efficient strategies to meet ever-expanding computational and data demands. This survey provides a comprehensive analysis of two complementary paradigms: Knowledge Distillation (KD) and Dataset Distillation (DD), both aimed at compressing LLMs while preserving their advanced reasoning capabilities and linguistic diversity. We first examine key methodologies in KD, such as task-specific alignment, rationale-based training, and multi-teacher frameworks, alongside DD techniques that synthesize compact, high-impact datasets through optimization-based gradient matching, latent space regularization, and generative synthesis. Building on these foundations, we explore how integrating KD and DD can produce more effective and scalable compression strategies. Together, these approaches address persistent challenges in model scalability, architectural heterogeneity, and the preservation of emergent LLM abilities. We further highlight applications across domains such as healthcare and education, where distillation enables efficient deployment without sacrificing performance. Despite substantial progress, open challenges remain in preserving emergent reasoning and linguistic diversity, enabling efficient adaptation to continually evolving teacher models and datasets, and establishing comprehensive evaluation protocols. By synthesizing methodological innovations, theoretical foundations, and practical insights, our survey charts a path toward sustainable, resource-efficient LLMs through the tighter integration of KD and DD principles.
ESPFormer: Doubly-Stochastic Attention with Expected Sliced Transport Plans
Feb 11, 2025Abstract:While self-attention has been instrumental in the success of Transformers, it can lead to over-concentration on a few tokens during training, resulting in suboptimal information flow. Enforcing doubly-stochastic constraints in attention matrices has been shown to improve structure and balance in attention distributions. However, existing methods rely on iterative Sinkhorn normalization, which is computationally costly. In this paper, we introduce a novel, fully parallelizable doubly-stochastic attention mechanism based on sliced optimal transport, leveraging Expected Sliced Transport Plans (ESP). Unlike prior approaches, our method enforces double stochasticity without iterative Sinkhorn normalization, significantly enhancing efficiency. To ensure differentiability, we incorporate a temperature-based soft sorting technique, enabling seamless integration into deep learning models. Experiments across multiple benchmark datasets, including image classification, point cloud classification, sentiment analysis, and neural machine translation, demonstrate that our enhanced attention regularization consistently improves performance across diverse applications.
Diffusion-Augmented Coreset Expansion for Scalable Dataset Distillation
Dec 05, 2024



Abstract:With the rapid scaling of neural networks, data storage and communication demands have intensified. Dataset distillation has emerged as a promising solution, condensing information from extensive datasets into a compact set of synthetic samples by solving a bilevel optimization problem. However, current methods face challenges in computational efficiency, particularly with high-resolution data and complex architectures. Recently, knowledge-distillation-based dataset condensation approaches have made this process more computationally feasible. Yet, with the recent developments of generative foundation models, there is now an opportunity to achieve even greater compression, enhance the quality of distilled data, and introduce valuable diversity into the data representation. In this work, we propose a two-stage solution. First, we compress the dataset by selecting only the most informative patches to form a coreset. Next, we leverage a generative foundation model to dynamically expand this compressed set in real-time, enhancing the resolution of these patches and introducing controlled variability to the coreset. Our extensive experiments demonstrate the robustness and efficiency of our approach across a range of dataset distillation benchmarks. We demonstrate a significant improvement of over 10% compared to the state-of-the-art on several large-scale dataset distillation benchmarks. The code will be released soon.
Understanding Learning with Sliced-Wasserstein Requires Rethinking Informative Slices
Nov 16, 2024Abstract:The practical applications of Wasserstein distances (WDs) are constrained by their sample and computational complexities. Sliced-Wasserstein distances (SWDs) provide a workaround by projecting distributions onto one-dimensional subspaces, leveraging the more efficient, closed-form WDs for one-dimensional distributions. However, in high dimensions, most random projections become uninformative due to the concentration of measure phenomenon. Although several SWD variants have been proposed to focus on \textit{informative} slices, they often introduce additional complexity, numerical instability, and compromise desirable theoretical (metric) properties of SWD. Amidst the growing literature that focuses on directly modifying the slicing distribution, which often face challenges, we revisit the classical Sliced-Wasserstein and propose instead to rescale the 1D Wasserstein to make all slices equally informative. Importantly, we show that with an appropriate data assumption and notion of \textit{slice informativeness}, rescaling for all individual slices simplifies to \textbf{a single global scaling factor} on the SWD. This, in turn, translates to the standard learning rate search for gradient-based learning in common machine learning workflows. We perform extensive experiments across various machine learning tasks showing that the classical SWD, when properly configured, can often match or surpass the performance of more complex variants. We then answer the following question: "Is Sliced-Wasserstein all you need for common learning tasks?"
Linear Spherical Sliced Optimal Transport: A Fast Metric for Comparing Spherical Data
Nov 09, 2024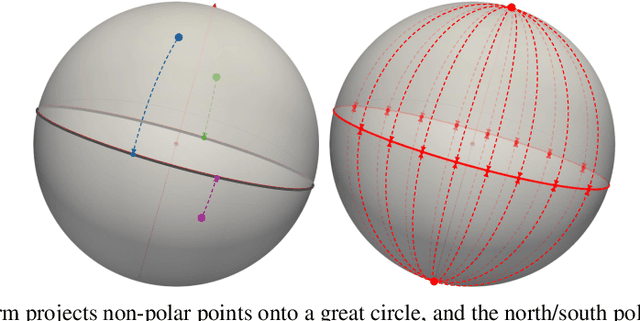
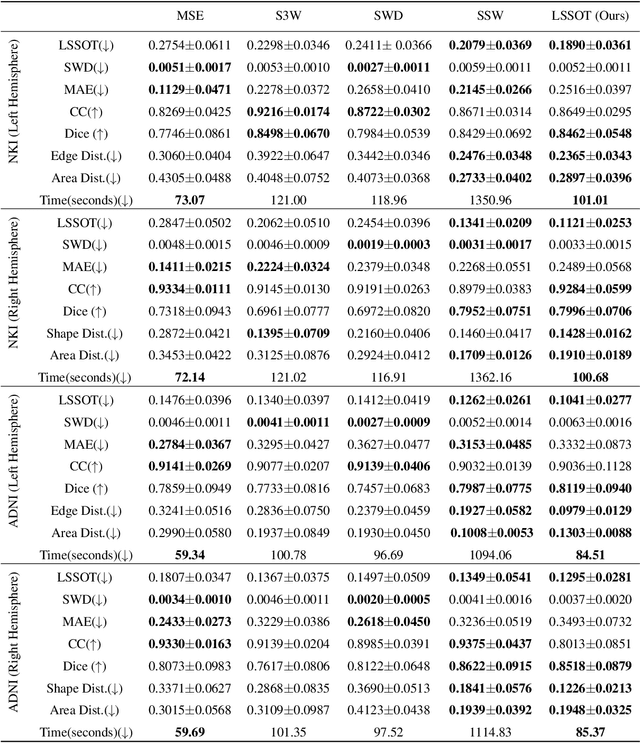
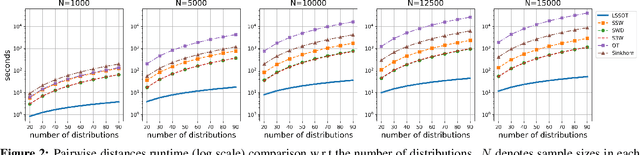
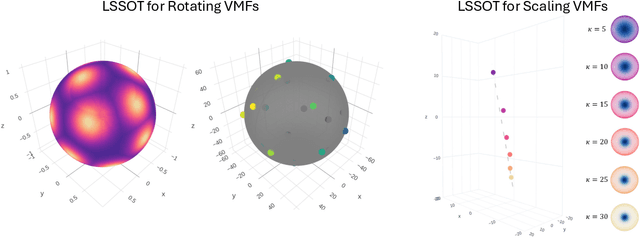
Abstract:Efficient comparison of spherical probability distributions becomes important in fields such as computer vision, geosciences, and medicine. Sliced optimal transport distances, such as spherical and stereographic spherical sliced Wasserstein distances, have recently been developed to address this need. These methods reduce the computational burden of optimal transport by slicing hyperspheres into one-dimensional projections, i.e., lines or circles. Concurrently, linear optimal transport has been proposed to embed distributions into \( L^2 \) spaces, where the \( L^2 \) distance approximates the optimal transport distance, thereby simplifying comparisons across multiple distributions. In this work, we introduce the Linear Spherical Sliced Optimal Transport (LSSOT) framework, which utilizes slicing to embed spherical distributions into \( L^2 \) spaces while preserving their intrinsic geometry, offering a computationally efficient metric for spherical probability measures. We establish the metricity of LSSOT and demonstrate its superior computational efficiency in applications such as cortical surface registration, 3D point cloud interpolation via gradient flow, and shape embedding. Our results demonstrate the significant computational benefits and high accuracy of LSSOT in these applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge