Collaborative Learning in Agentic Systems: A Collective AI is Greater Than the Sum of Its Parts

Agentic AI has gained significant interest as a research paradigm focused on autonomy, self-directed learning, and long-term reliability of decision making. Real-world agentic systems operate in decentralized settings on a large set of tasks or data distributions with constraints such as limited bandwidth, asynchronous execution, and the absence of a centralized model or even common objectives. We posit that exploiting previously learned skills, task similarities, and communication capabilities in a collective of agentic AI are challenging but essential elements to enabling scalability, open-endedness, and beneficial collaborative learning dynamics. In this paper, we introduce Modular Sharing and Composition in Collective Learning (MOSAIC), an agentic algorithm that allows multiple agents to independently solve different tasks while also identifying, sharing, and reusing useful machine-learned knowledge, without coordination, synchronization, or centralized control. MOSAIC combines three mechanisms: (1) modular policy composition via neural network masks, (2) cosine similarity estimation using Wasserstein embeddings for knowledge selection, and (3) asynchronous communication and policy integration. Results on a set of RL benchmarks show that MOSAIC has a greater sample efficiency than isolated learners, i.e., it learns significantly faster, and in some cases, finds solutions to tasks that cannot be solved by isolated learners. The collaborative learning and sharing dynamics are also observed to result in the emergence of ideal curricula of tasks, from easy to hard. These findings support the case for collaborative learning in agentic systems to achieve better and continuously evolving performance both at the individual and collective levels.

FutureSightDrive: Thinking Visually with Spatio-Temporal CoT for Autonomous Driving

Visual language models (VLMs) have attracted increasing interest in autonomous driving due to their powerful reasoning capabilities. However, existing VLMs typically utilize discrete text Chain-of-Thought (CoT) tailored to the current scenario, which essentially represents highly abstract and symbolic compression of visual information, potentially leading to spatio-temporal relationship ambiguity and fine-grained information loss. Is autonomous driving better modeled on real-world simulation and imagination than on pure symbolic logic? In this paper, we propose a spatio-temporal CoT reasoning method that enables models to think visually. First, VLM serves as a world model to generate unified image frame for predicting future world states: where perception results (e.g., lane divider and 3D detection) represent the future spatial relationships, and ordinary future frame represent the temporal evolution relationships. This spatio-temporal CoT then serves as intermediate reasoning steps, enabling the VLM to function as an inverse dynamics model for trajectory planning based on current observations and future predictions. To implement visual generation in VLMs, we propose a unified pretraining paradigm integrating visual generation and understanding, along with a progressive visual CoT enhancing autoregressive image generation. Extensive experimental results demonstrate the effectiveness of the proposed method, advancing autonomous driving towards visual reasoning.

Accelerated Quasi-Static FEM for Real-Time Modeling of Continuum Robots with Multiple Contacts and Large Deformation

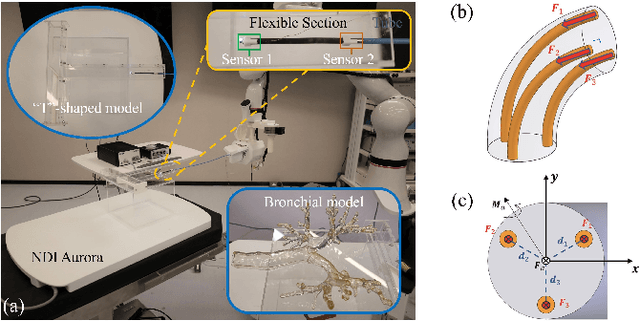
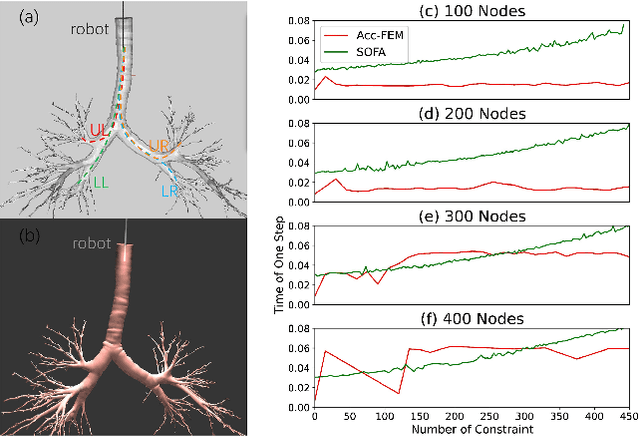
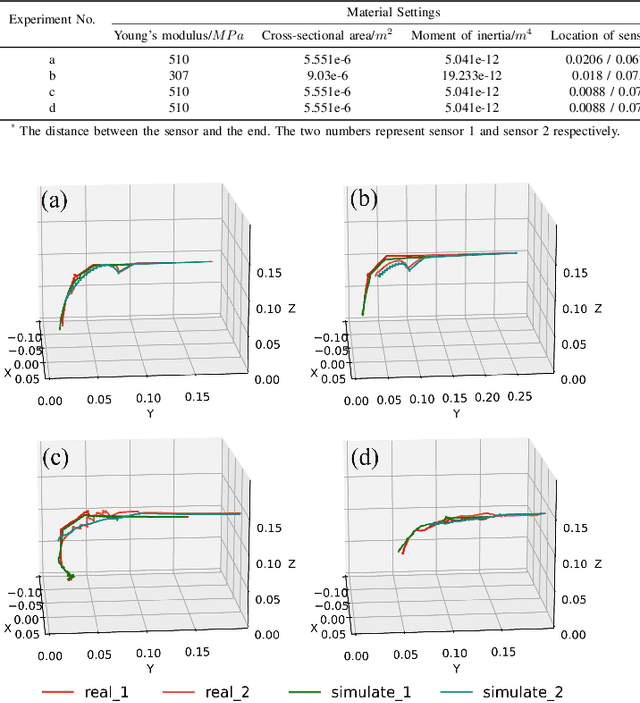
Continuum robots offer high flexibility and multiple degrees of freedom, making them ideal for navigating narrow lumens. However, accurately modeling their behavior under large deformations and frequent environmental contacts remains challenging. Current methods for solving the deformation of these robots, such as the Model Order Reduction and Gauss-Seidel (GS) methods, suffer from significant drawbacks. They experience reduced computational speed as the number of contact points increases and struggle to balance speed with model accuracy. To overcome these limitations, we introduce a novel finite element method (FEM) named Acc-FEM. Acc-FEM employs a large deformation quasi-static finite element model and integrates an accelerated solver scheme to handle multi-contact simulations efficiently. Additionally, it utilizes parallel computing with Graphics Processing Units (GPU) for real-time updates of the finite element models and collision detection. Extensive numerical experiments demonstrate that Acc-FEM significantly improves computational efficiency in modeling continuum robots with multiple contacts while achieving satisfactory accuracy, addressing the deficiencies of existing methods.

DGFM: Full Body Dance Generation Driven by Music Foundation Models

In music-driven dance motion generation, most existing methods use hand-crafted features and neglect that music foundation models have profoundly impacted cross-modal content generation. To bridge this gap, we propose a diffusion-based method that generates dance movements conditioned on text and music. Our approach extracts music features by combining high-level features obtained by music foundation model with hand-crafted features, thereby enhancing the quality of generated dance sequences. This method effectively leverages the advantages of high-level semantic information and low-level temporal details to improve the model's capability in music feature understanding. To show the merits of the proposed method, we compare it with four music foundation models and two sets of hand-crafted music features. The results demonstrate that our method obtains the most realistic dance sequences and achieves the best match with the input music.

GCDance: Genre-Controlled 3D Full Body Dance Generation Driven By Music

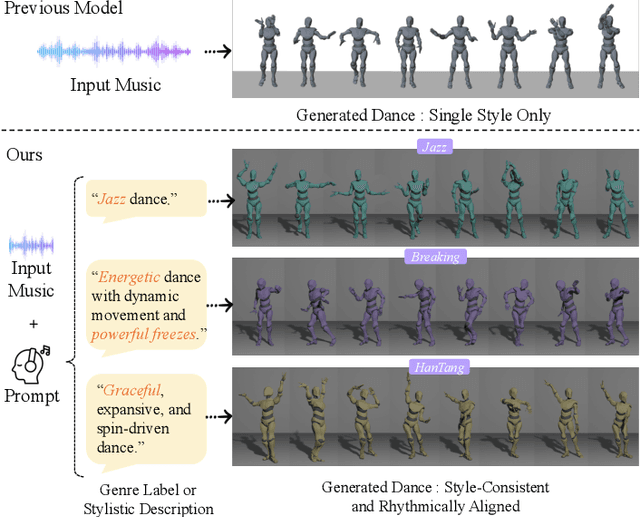
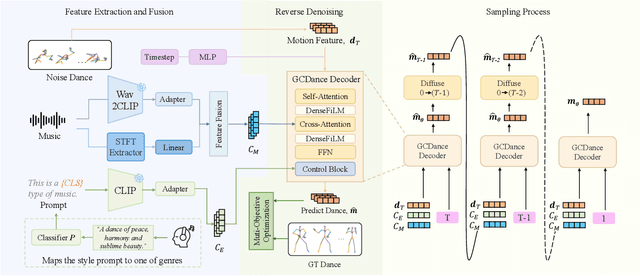
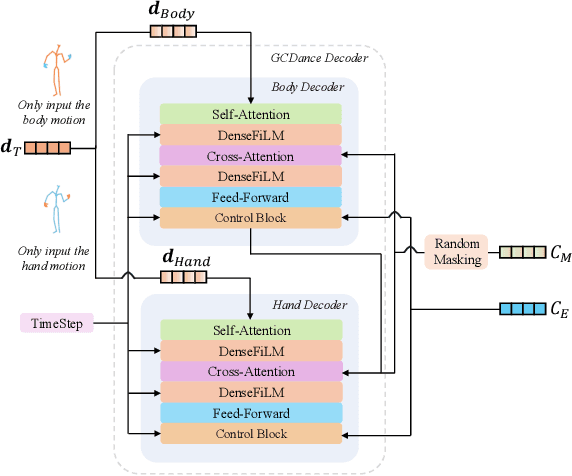
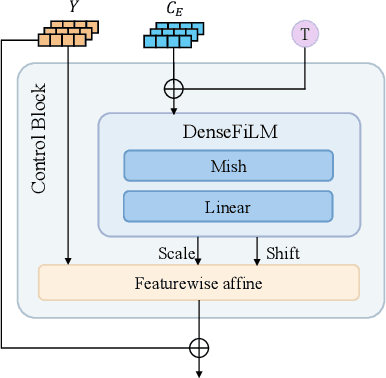
Generating high-quality full-body dance sequences from music is a challenging task as it requires strict adherence to genre-specific choreography. Moreover, the generated sequences must be both physically realistic and precisely synchronized with the beats and rhythm of the music. To overcome these challenges, we propose GCDance, a classifier-free diffusion framework for generating genre-specific dance motions conditioned on both music and textual prompts. Specifically, our approach extracts music features by combining high-level pre-trained music foundation model features with hand-crafted features for multi-granularity feature fusion. To achieve genre controllability, we leverage CLIP to efficiently embed genre-based textual prompt representations at each time step within our dance generation pipeline. Our GCDance framework can generate diverse dance styles from the same piece of music while ensuring coherence with the rhythm and melody of the music. Extensive experimental results obtained on the FineDance dataset demonstrate that GCDance significantly outperforms the existing state-of-the-art approaches, which also achieve competitive results on the AIST++ dataset. Our ablation and inference time analysis demonstrate that GCDance provides an effective solution for high-quality music-driven dance generation.

ESPFormer: Doubly-Stochastic Attention with Expected Sliced Transport Plans

While self-attention has been instrumental in the success of Transformers, it can lead to over-concentration on a few tokens during training, resulting in suboptimal information flow. Enforcing doubly-stochastic constraints in attention matrices has been shown to improve structure and balance in attention distributions. However, existing methods rely on iterative Sinkhorn normalization, which is computationally costly. In this paper, we introduce a novel, fully parallelizable doubly-stochastic attention mechanism based on sliced optimal transport, leveraging Expected Sliced Transport Plans (ESP). Unlike prior approaches, our method enforces double stochasticity without iterative Sinkhorn normalization, significantly enhancing efficiency. To ensure differentiability, we incorporate a temperature-based soft sorting technique, enabling seamless integration into deep learning models. Experiments across multiple benchmark datasets, including image classification, point cloud classification, sentiment analysis, and neural machine translation, demonstrate that our enhanced attention regularization consistently improves performance across diverse applications.

Linear Spherical Sliced Optimal Transport: A Fast Metric for Comparing Spherical Data

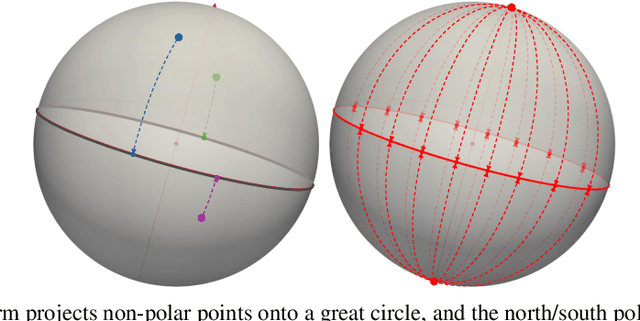
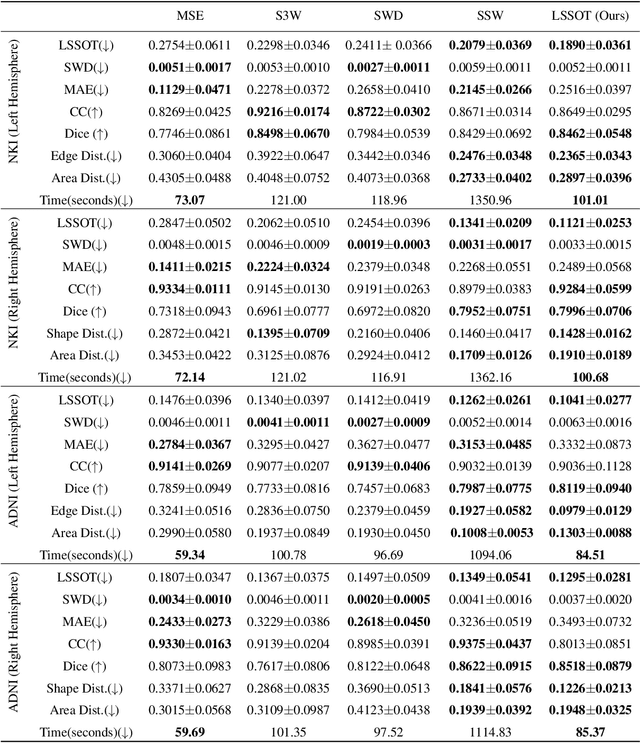
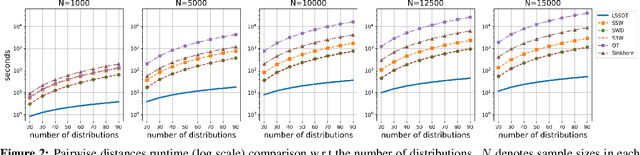
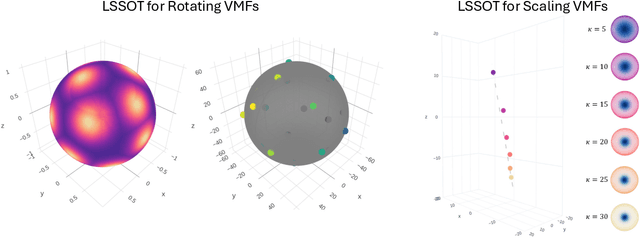
Efficient comparison of spherical probability distributions becomes important in fields such as computer vision, geosciences, and medicine. Sliced optimal transport distances, such as spherical and stereographic spherical sliced Wasserstein distances, have recently been developed to address this need. These methods reduce the computational burden of optimal transport by slicing hyperspheres into one-dimensional projections, i.e., lines or circles. Concurrently, linear optimal transport has been proposed to embed distributions into \( L^2 \) spaces, where the \( L^2 \) distance approximates the optimal transport distance, thereby simplifying comparisons across multiple distributions. In this work, we introduce the Linear Spherical Sliced Optimal Transport (LSSOT) framework, which utilizes slicing to embed spherical distributions into \( L^2 \) spaces while preserving their intrinsic geometry, offering a computationally efficient metric for spherical probability measures. We establish the metricity of LSSOT and demonstrate its superior computational efficiency in applications such as cortical surface registration, 3D point cloud interpolation via gradient flow, and shape embedding. Our results demonstrate the significant computational benefits and high accuracy of LSSOT in these applications.

Driving by the Rules: A Benchmark for Integrating Traffic Sign Regulations into Vectorized HD Map

Ensuring adherence to traffic sign regulations is essential for both human and autonomous vehicle navigation. While current benchmark datasets concentrate on lane perception or basic traffic sign recognition, they often overlook the intricate task of integrating these regulations into lane operations. Addressing this gap, we introduce MapDR, a novel dataset designed for the extraction of Driving Rules from traffic signs and their association with vectorized, locally perceived HD Maps. MapDR features over 10,000 annotated video clips that capture the intricate correlation between traffic sign regulations and lanes. We define two pivotal sub-tasks: 1) Rule Extraction from Traffic Sign, which accurately deciphers regulatory instructions, and 2) Rule-Lane Correspondence Reasoning, which aligns these rules with their respective lanes. Built upon this benchmark, we provide a multimodal solution that offers a strong baseline for advancing autonomous driving technologies. It fills a critical gap in the integration of traffic sign rules, contributing to the development of reliable autonomous navigation systems.

Expected Sliced Transport Plans

The optimal transport (OT) problem has gained significant traction in modern machine learning for its ability to: (1) provide versatile metrics, such as Wasserstein distances and their variants, and (2) determine optimal couplings between probability measures. To reduce the computational complexity of OT solvers, methods like entropic regularization and sliced optimal transport have been proposed. The sliced OT framework improves efficiency by comparing one-dimensional projections (slices) of high-dimensional distributions. However, despite their computational efficiency, sliced-Wasserstein approaches lack a transportation plan between the input measures, limiting their use in scenarios requiring explicit coupling. In this paper, we address two key questions: Can a transportation plan be constructed between two probability measures using the sliced transport framework? If so, can this plan be used to define a metric between the measures? We propose a "lifting" operation to extend one-dimensional optimal transport plans back to the original space of the measures. By computing the expectation of these lifted plans, we derive a new transportation plan, termed expected sliced transport (EST) plans. We prove that using the EST plan to weight the sum of the individual Euclidean costs for moving from one point to another results in a valid metric between the input discrete probability measures. We demonstrate the connection between our approach and the recently proposed min-SWGG, along with illustrative numerical examples that support our theoretical findings.

Driving with Prior Maps: Unified Vector Prior Encoding for Autonomous Vehicle Mapping

High-Definition Maps (HD maps) are essential for the precise navigation and decision-making of autonomous vehicles, yet their creation and upkeep present significant cost and timeliness challenges. The online construction of HD maps using on-board sensors has emerged as a promising solution; however, these methods can be impeded by incomplete data due to occlusions and inclement weather. This paper proposes the PriorDrive framework to addresses these limitations by harnessing the power of prior maps, significantly enhancing the robustness and accuracy of online HD map construction. Our approach integrates a variety of prior maps, such as OpenStreetMap's Standard Definition Maps (SD maps), outdated HD maps from vendors, and locally constructed maps from historical vehicle data. To effectively encode this prior information into online mapping models, we introduce a Hybrid Prior Representation (HPQuery) that standardizes the representation of diverse map elements. At the core of PriorDrive is the Unified Vector Encoder (UVE), which employs a dual encoding mechanism to process vector data. The intra-vector encoder captures fine-grained local features, while the inter-vector encoder integrates global context. Furthermore, we propose a segment-level and point-level pre-training strategy that enables the UVE to learn the prior distribution of vector data, thereby improving the encoder's generalizability and performance. Through extensive testing on the nuScenes dataset, we demonstrate that PriorDrive is highly compatible with various online mapping models and substantially improves map prediction capabilities. The integration of prior maps through the PriorDrive framework offers a robust solution to the challenges of single-perception data, paving the way for more reliable autonomous vehicle navigation.