Diffusion-Augmented Coreset Expansion for Scalable Dataset Distillation

With the rapid scaling of neural networks, data storage and communication demands have intensified. Dataset distillation has emerged as a promising solution, condensing information from extensive datasets into a compact set of synthetic samples by solving a bilevel optimization problem. However, current methods face challenges in computational efficiency, particularly with high-resolution data and complex architectures. Recently, knowledge-distillation-based dataset condensation approaches have made this process more computationally feasible. Yet, with the recent developments of generative foundation models, there is now an opportunity to achieve even greater compression, enhance the quality of distilled data, and introduce valuable diversity into the data representation. In this work, we propose a two-stage solution. First, we compress the dataset by selecting only the most informative patches to form a coreset. Next, we leverage a generative foundation model to dynamically expand this compressed set in real-time, enhancing the resolution of these patches and introducing controlled variability to the coreset. Our extensive experiments demonstrate the robustness and efficiency of our approach across a range of dataset distillation benchmarks. We demonstrate a significant improvement of over 10% compared to the state-of-the-art on several large-scale dataset distillation benchmarks. The code will be released soon.

Next-Token Prediction Task Assumes Optimal Data Ordering for LLM Training in Proof Generation

In the field of large language model (LLM)-based proof generation, despite being trained on extensive corpora such as OpenWebMath and Arxiv, these models still exhibit only modest performance on proving tasks of moderate difficulty. We believe that this is partly due to the suboptimal order of each proof data used in training. Published proofs often follow a purely logical order, where each step logically proceeds from the previous steps based on the deductive rules. However, this order aims to facilitate the verification of the proof's soundness, rather than to help people and models learn the discovery process of the proof. In proof generation, we argue that the optimal order for one training data sample occurs when the relevant intermediate supervision for a particular proof step in the proof is always positioned to the left of that proof step. We call such order the intuitively sequential order. We validate our claims using two tasks: intuitionistic propositional logic theorem-proving and digit multiplication. Our experiments verify the order effect and provide support for our explanations. We demonstrate that training is most effective when the proof is in the intuitively sequential order. Moreover, the order effect and the performance gap between models trained on different data orders are substantial -- with an 11 percent improvement in proof success rate observed in the propositional logic theorem-proving task, between models trained on the optimal order compared to the worst order.

Generative Kaleidoscopic Networks

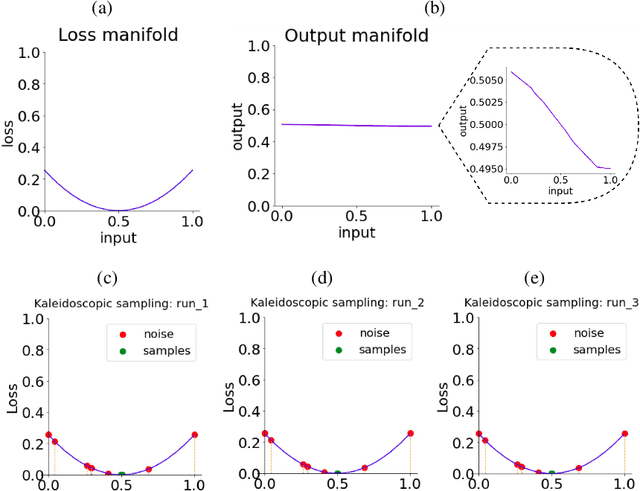
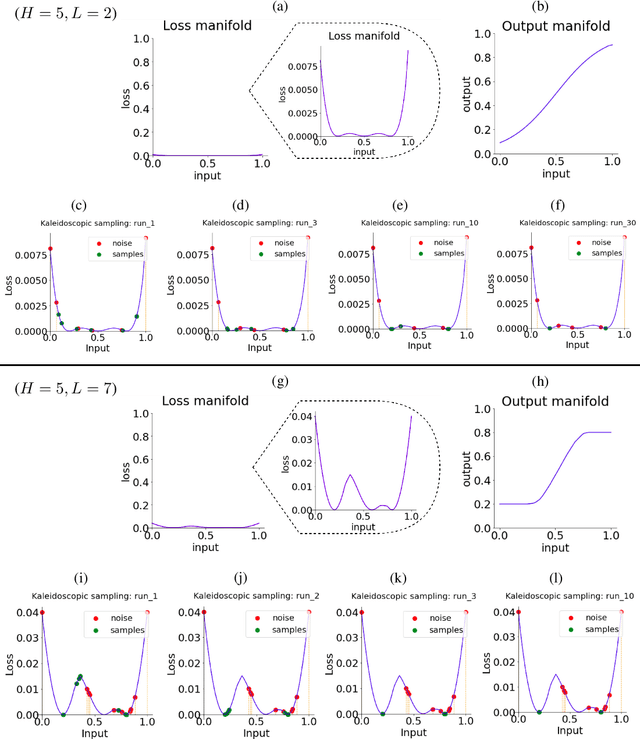
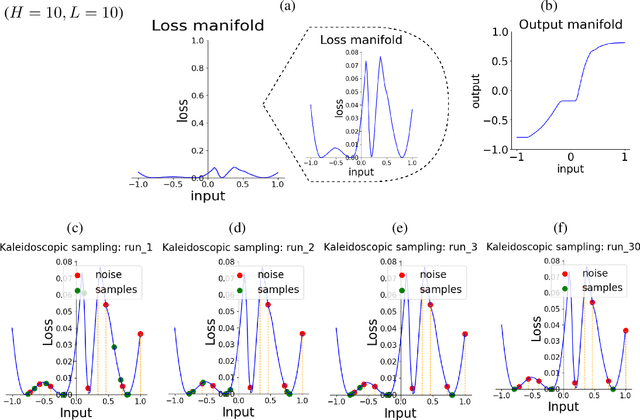
We discovered that the neural networks, especially the deep ReLU networks, demonstrate an `over-generalization' phenomenon. That is, the output values for the inputs that were not seen during training are mapped close to the output range that were observed during the learning process. In other words, the neural networks learn a many-to-one mapping and this effect is more prominent as we increase the number of layers or the depth of the neural network. We utilize this property of neural networks to design a dataset kaleidoscope, termed as `Generative Kaleidoscopic Networks'. Briefly, if we learn a model to map from input $x\in\mathbb{R}^D$ to itself $f_\mathcal{N}(x)\rightarrow x$, the proposed `Kaleidoscopic sampling' procedure starts with a random input noise $z\in\mathbb{R}^D$ and recursively applies $f_\mathcal{N}(\cdots f_\mathcal{N}(z)\cdots )$. After a burn-in period duration, we start observing samples from the input distribution and the quality of samples recovered improves as we increase the depth of the model. Scope: We observed this phenomenon to various degrees for the other deep learning architectures like CNNs, Transformers & U-Nets and we are currently investigating them further.

Federated Learning with Neural Graphical Models

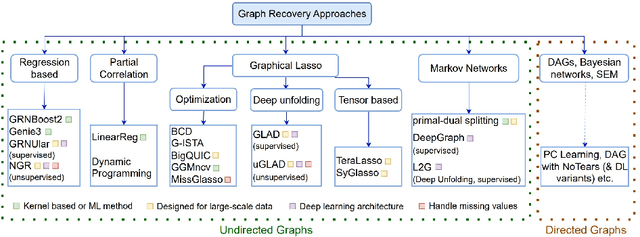
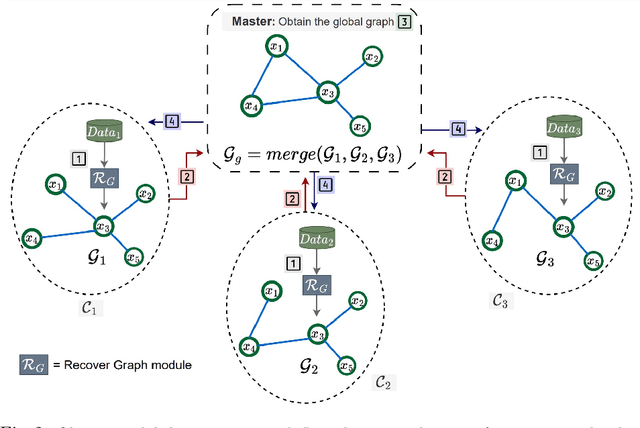
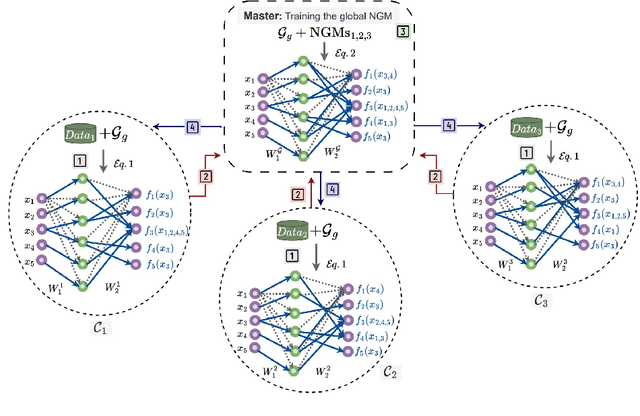
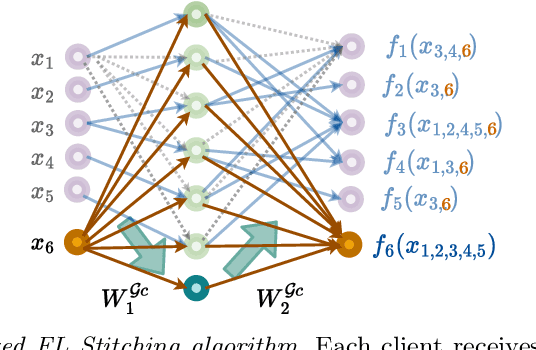
Federated Learning (FL) addresses the need to create models based on proprietary data in such a way that multiple clients retain exclusive control over their data, while all benefit from improved model accuracy due to pooled resources. Recently proposed Neural Graphical Models (NGMs) are Probabilistic Graphical models that utilize the expressive power of neural networks to learn complex non-linear dependencies between the input features. They learn to capture the underlying data distribution and have efficient algorithms for inference and sampling. We develop a FL framework which maintains a global NGM model that learns the averaged information from the local NGM models while keeping the training data within the client's environment. Our design, FedNGMs, avoids the pitfalls and shortcomings of neuron matching frameworks like Federated Matched Averaging that suffers from model parameter explosion. Our global model size remains constant throughout the process. In the cases where clients have local variables that are not part of the combined global distribution, we propose a `Stitching' algorithm, which personalizes the global NGM models by merging the additional variables using the client's data. FedNGM is robust to data heterogeneity, large number of participants, and limited communication bandwidth.

Knowledge Propagation over Conditional Independence Graphs

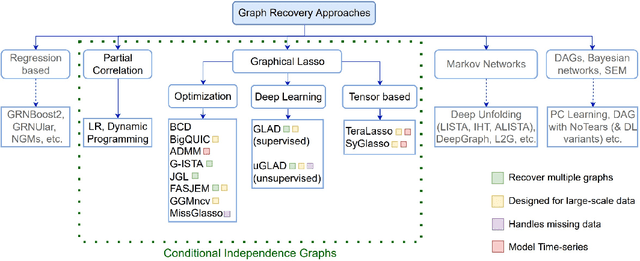
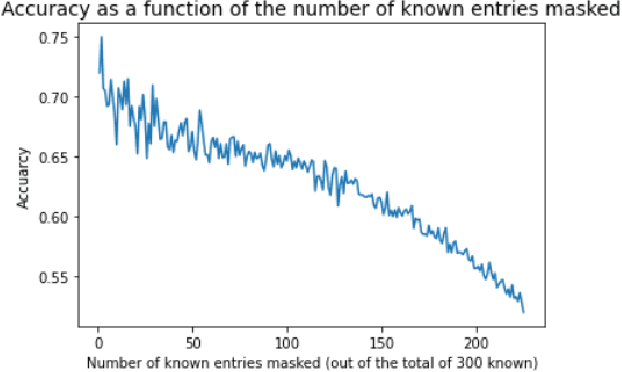
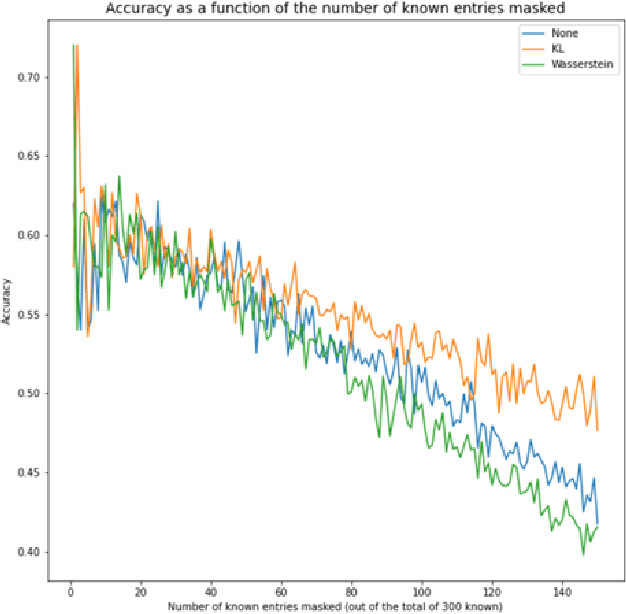
Conditional Independence (CI) graph is a special type of a Probabilistic Graphical Model (PGM) where the feature connections are modeled using an undirected graph and the edge weights show the partial correlation strength between the features. Since the CI graphs capture direct dependence between features, they have been garnering increasing interest within the research community for gaining insights into the systems from various domains, in particular discovering the domain topology. In this work, we propose algorithms for performing knowledge propagation over the CI graphs. Our experiments demonstrate that our techniques improve upon the state-of-the-art on the publicly available Cora and PubMed datasets.

DiversiGATE: A Comprehensive Framework for Reliable Large Language Models

In this paper, we introduce DiversiGATE, a unified framework that consolidates diverse methodologies for LLM verification. The proposed framework comprises two main components: Diversification and Aggregation which provide a holistic perspective on existing verification approaches, such as Self-Consistency, Math Prompter and WebGPT. Furthermore, we propose a novel `SelfLearner' model that conforms to the DiversiGATE framework which can learn from its own outputs and refine its performance over time, leading to improved accuracy. To evaluate the effectiveness of SelfLearner, we conducted a rigorous series of experiments, including tests on synthetic data as well as on popular arithmetic reasoning benchmarks such as GSM8K. Our results demonstrate that our approach outperforms traditional LLMs, achieving a considerable 54.8% -> 61.8% improvement on the GSM8K benchmark.

Are uGLAD? Time will tell!

We frequently encounter multiple series that are temporally correlated in our surroundings, such as EEG data to examine alterations in brain activity or sensors to monitor body movements. Segmentation of multivariate time series data is a technique for identifying meaningful patterns or changes in the time series that can signal a shift in the system's behavior. However, most segmentation algorithms have been designed primarily for univariate time series, and their performance on multivariate data remains largely unsatisfactory, making this a challenging problem. In this work, we introduce a novel approach for multivariate time series segmentation using conditional independence (CI) graphs. CI graphs are probabilistic graphical models that represents the partial correlations between the nodes. We propose a domain agnostic multivariate segmentation framework `$\texttt{tGLAD}$' which draws a parallel between the CI graph nodes and the variables of the time series. Consider applying a graph recovery model $\texttt{uGLAD}$ to a short interval of the time series, it will result in a CI graph that shows partial correlations among the variables. We extend this idea to the entire time series by utilizing a sliding window to create a batch of time intervals and then run a single $\texttt{uGLAD}$ model in multitask learning mode to recover all the CI graphs simultaneously. As a result, we obtain a corresponding temporal CI graphs representation. We then designed a first-order and second-order based trajectory tracking algorithms to study the evolution of these graphs across distinct intervals. Finally, an `Allocation' algorithm is used to determine a suitable segmentation of the temporal graph sequence. $\texttt{tGLAD}$ provides a competitive time complexity of $O(N)$ for settings where number of variables $D<<N$. We demonstrate successful empirical results on a Physical Activity Monitoring data.

MathPrompter: Mathematical Reasoning using Large Language Models

Large Language Models (LLMs) have limited performance when solving arithmetic reasoning tasks and often provide incorrect answers. Unlike natural language understanding, math problems typically have a single correct answer, making the task of generating accurate solutions more challenging for LLMs. To the best of our knowledge, we are not aware of any LLMs that indicate their level of confidence in their responses which fuels a trust deficit in these models impeding their adoption. To address this deficiency, we propose `MathPrompter', a technique that improves performance of LLMs on arithmetic problems along with increased reliance in the predictions. MathPrompter uses the Zero-shot chain-of-thought prompting technique to generate multiple Algebraic expressions or Python functions to solve the same math problem in different ways and thereby raise the confidence level in the output results. This is in contrast to other prompt based CoT methods, where there is no check on the validity of the intermediate steps followed. Our technique improves over state-of-the-art on the MultiArith dataset ($78.7\%\rightarrow92.5\%$) evaluated using 175B parameter GPT-based LLM.

Neural Graph Revealers

Sparse graph recovery methods work well where the data follows their assumptions but often they are not designed for doing downstream probabilistic queries. This limits their adoption to only identifying connections among the input variables. On the other hand, the Probabilistic Graphical Models (PGMs) assume an underlying base graph between variables and learns a distribution over them. PGM design choices are carefully made such that the inference \& sampling algorithms are efficient. This brings in certain restrictions and often simplifying assumptions. In this work, we propose Neural Graph Revealers (NGRs), that are an attempt to efficiently merge the sparse graph recovery methods with PGMs into a single flow. The problem setting consists of an input data X with D features and M samples and the task is to recover a sparse graph showing connection between the features and learn a probability distribution over the D at the same time. NGRs view the neural networks as a `glass box' or more specifically as a multitask learning framework. We introduce `Graph-constrained path norm' that NGRs leverage to learn a graphical model that captures complex non-linear functional dependencies between the features in the form of an undirected sparse graph. Furthermore, NGRs can handle multimodal inputs like images, text, categorical data, embeddings etc. which is not straightforward to incorporate in the existing methods. We show experimental results of doing sparse graph recovery and probabilistic inference on data from Gaussian graphical models and a multimodal infant mortality dataset by Centers for Disease Control and Prevention.

Methods for Recovering Conditional Independence Graphs: A Survey

Conditional Independence (CI) graphs are a type of probabilistic graphical models that are primarily used to gain insights about feature relationships. Each edge represents the partial correlation between the connected features which gives information about their direct dependence. In this survey, we list out different methods and study the advances in techniques developed to recover CI graphs. We cover traditional optimization methods as well as recently developed deep learning architectures along with their recommended implementations. To facilitate wider adoption, we include preliminaries that consolidate associated operations, for example techniques to obtain covariance matrix for mixed datatypes.