Federated Learning with Neural Graphical Models

Federated Learning (FL) addresses the need to create models based on proprietary data in such a way that multiple clients retain exclusive control over their data, while all benefit from improved model accuracy due to pooled resources. Recently proposed Neural Graphical Models (NGMs) are Probabilistic Graphical models that utilize the expressive power of neural networks to learn complex non-linear dependencies between the input features. They learn to capture the underlying data distribution and have efficient algorithms for inference and sampling. We develop a FL framework which maintains a global NGM model that learns the averaged information from the local NGM models while keeping the training data within the client's environment. Our design, FedNGMs, avoids the pitfalls and shortcomings of neuron matching frameworks like Federated Matched Averaging that suffers from model parameter explosion. Our global model size remains constant throughout the process. In the cases where clients have local variables that are not part of the combined global distribution, we propose a `Stitching' algorithm, which personalizes the global NGM models by merging the additional variables using the client's data. FedNGM is robust to data heterogeneity, large number of participants, and limited communication bandwidth.

Knowledge Propagation over Conditional Independence Graphs

Conditional Independence (CI) graph is a special type of a Probabilistic Graphical Model (PGM) where the feature connections are modeled using an undirected graph and the edge weights show the partial correlation strength between the features. Since the CI graphs capture direct dependence between features, they have been garnering increasing interest within the research community for gaining insights into the systems from various domains, in particular discovering the domain topology. In this work, we propose algorithms for performing knowledge propagation over the CI graphs. Our experiments demonstrate that our techniques improve upon the state-of-the-art on the publicly available Cora and PubMed datasets.

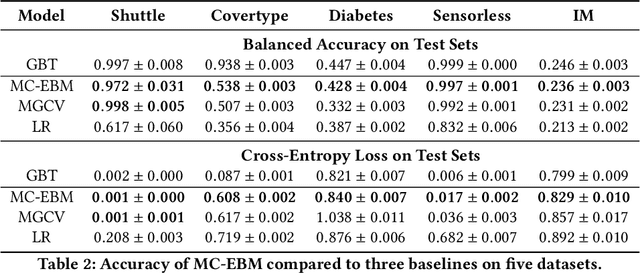
Missing Values and Imputation in Healthcare Data: Can Interpretable Machine Learning Help?

Missing values are a fundamental problem in data science. Many datasets have missing values that must be properly handled because the way missing values are treated can have large impact on the resulting machine learning model. In medical applications, the consequences may affect healthcare decisions. There are many methods in the literature for dealing with missing values, including state-of-the-art methods which often depend on black-box models for imputation. In this work, we show how recent advances in interpretable machine learning provide a new perspective for understanding and tackling the missing value problem. We propose methods based on high-accuracy glass-box Explainable Boosting Machines (EBMs) that can help users (1) gain new insights on missingness mechanisms and better understand the causes of missingness, and (2) detect -- or even alleviate -- potential risks introduced by imputation algorithms. Experiments on real-world medical datasets illustrate the effectiveness of the proposed methods.

Neural Graph Revealers

Sparse graph recovery methods work well where the data follows their assumptions but often they are not designed for doing downstream probabilistic queries. This limits their adoption to only identifying connections among the input variables. On the other hand, the Probabilistic Graphical Models (PGMs) assume an underlying base graph between variables and learns a distribution over them. PGM design choices are carefully made such that the inference \& sampling algorithms are efficient. This brings in certain restrictions and often simplifying assumptions. In this work, we propose Neural Graph Revealers (NGRs), that are an attempt to efficiently merge the sparse graph recovery methods with PGMs into a single flow. The problem setting consists of an input data X with D features and M samples and the task is to recover a sparse graph showing connection between the features and learn a probability distribution over the D at the same time. NGRs view the neural networks as a `glass box' or more specifically as a multitask learning framework. We introduce `Graph-constrained path norm' that NGRs leverage to learn a graphical model that captures complex non-linear functional dependencies between the features in the form of an undirected sparse graph. Furthermore, NGRs can handle multimodal inputs like images, text, categorical data, embeddings etc. which is not straightforward to incorporate in the existing methods. We show experimental results of doing sparse graph recovery and probabilistic inference on data from Gaussian graphical models and a multimodal infant mortality dataset by Centers for Disease Control and Prevention.

Methods for Recovering Conditional Independence Graphs: A Survey

Conditional Independence (CI) graphs are a type of probabilistic graphical models that are primarily used to gain insights about feature relationships. Each edge represents the partial correlation between the connected features which gives information about their direct dependence. In this survey, we list out different methods and study the advances in techniques developed to recover CI graphs. We cover traditional optimization methods as well as recently developed deep learning architectures along with their recommended implementations. To facilitate wider adoption, we include preliminaries that consolidate associated operations, for example techniques to obtain covariance matrix for mixed datatypes.

Neural Graphical Models

Graphs are ubiquitous and are often used to understand the dynamics of a system. Probabilistic Graphical Models comprising Bayesian and Markov networks, and Conditional Independence graphs are some of the popular graph representation techniques. They can model relationships between features (nodes) together with the underlying distribution. Although theoretically these models can represent very complex dependency functions, in practice often simplifying assumptions are made due to computational limitations associated with graph operations. This work introduces Neural Graphical Models (NGMs) which attempt to represent complex feature dependencies with reasonable computational costs. Specifically, given a graph of feature relationships and corresponding samples, we capture the dependency structure between the features along with their complex function representations by using neural networks as a multi-task learning framework. We provide efficient learning, inference and sampling algorithms for NGMs. Moreover, NGMs can fit generic graph structures including directed, undirected and mixed-edge graphs as well as support mixed input data types. We present empirical studies that show NGMs' capability to represent Gaussian graphical models, inference analysis of a lung cancer data and extract insights from a real world infant mortality data provided by CDC.

uGLAD: Sparse graph recovery by optimizing deep unrolled networks

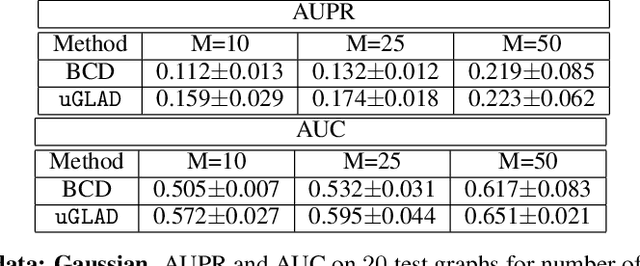
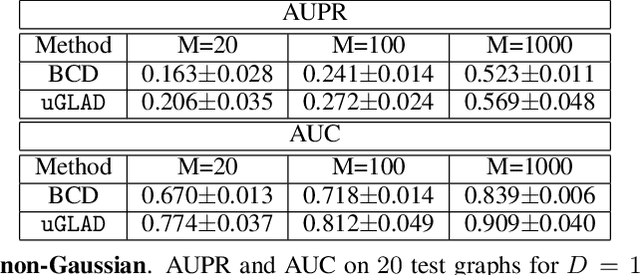
Probabilistic Graphical Models (PGMs) are generative models of complex systems. They rely on conditional independence assumptions between variables to learn sparse representations which can be visualized in a form of a graph. Such models are used for domain exploration and structure discovery in poorly understood domains. This work introduces a novel technique to perform sparse graph recovery by optimizing deep unrolled networks. Assuming that the input data $X\in\mathbb{R}^{M\times D}$ comes from an underlying multivariate Gaussian distribution, we apply a deep model on $X$ that outputs the precision matrix $\Theta$, which can also be interpreted as the adjacency matrix. Our model, uGLAD, builds upon and extends the state-of-the-art model GLAD to the unsupervised setting. The key benefits of our model are (1) uGLAD automatically optimizes sparsity-related regularization parameters leading to better performance than existing algorithms. (2) We introduce multi-task learning based `consensus' strategy for robust handling of missing data in an unsupervised setting. We evaluate model results on synthetic Gaussian data, non-Gaussian data generated from Gene Regulatory Networks, and present a case study in anaerobic digestion.

Discovering Distribution Shifts using Latent Space Representations

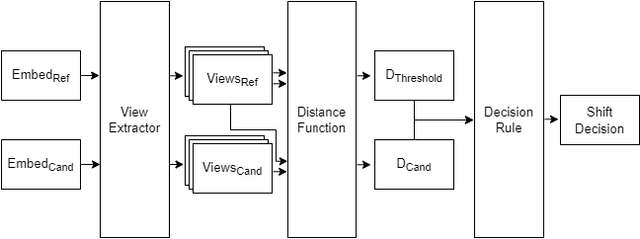
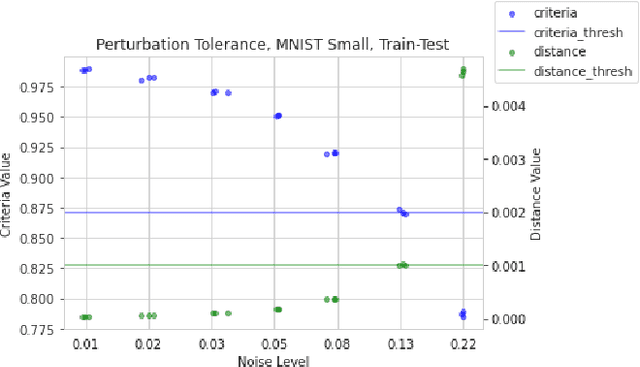
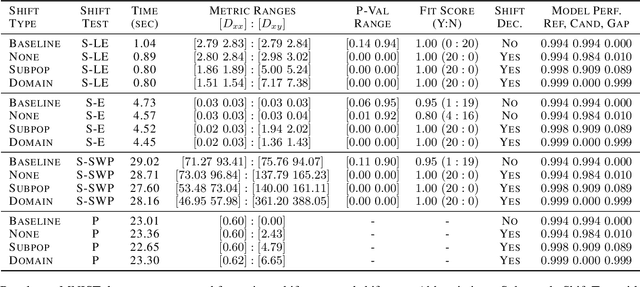
Rapid progress in representation learning has led to a proliferation of embedding models, and to associated challenges of model selection and practical application. It is non-trivial to assess a model's generalizability to new, candidate datasets and failure to generalize may lead to poor performance on downstream tasks. Distribution shifts are one cause of reduced generalizability, and are often difficult to detect in practice. In this paper, we use the embedding space geometry to propose a non-parametric framework for detecting distribution shifts, and specify two tests. The first test detects shifts by establishing a robustness boundary, determined by an intelligible performance criterion, for comparing reference and candidate datasets. The second test detects shifts by featurizing and classifying multiple subsamples of two datasets as in-distribution and out-of-distribution. In evaluation, both tests detect model-impacting distribution shifts, in various shift scenarios, for both synthetic and real-world datasets.

Interpretability is Harder in the Multiclass Setting: Axiomatic Interpretability for Multiclass Additive Models

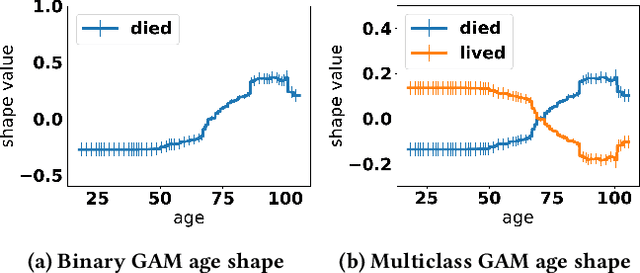
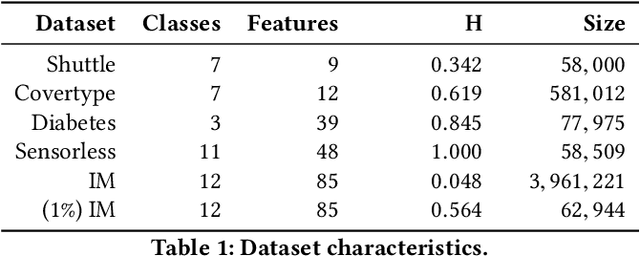
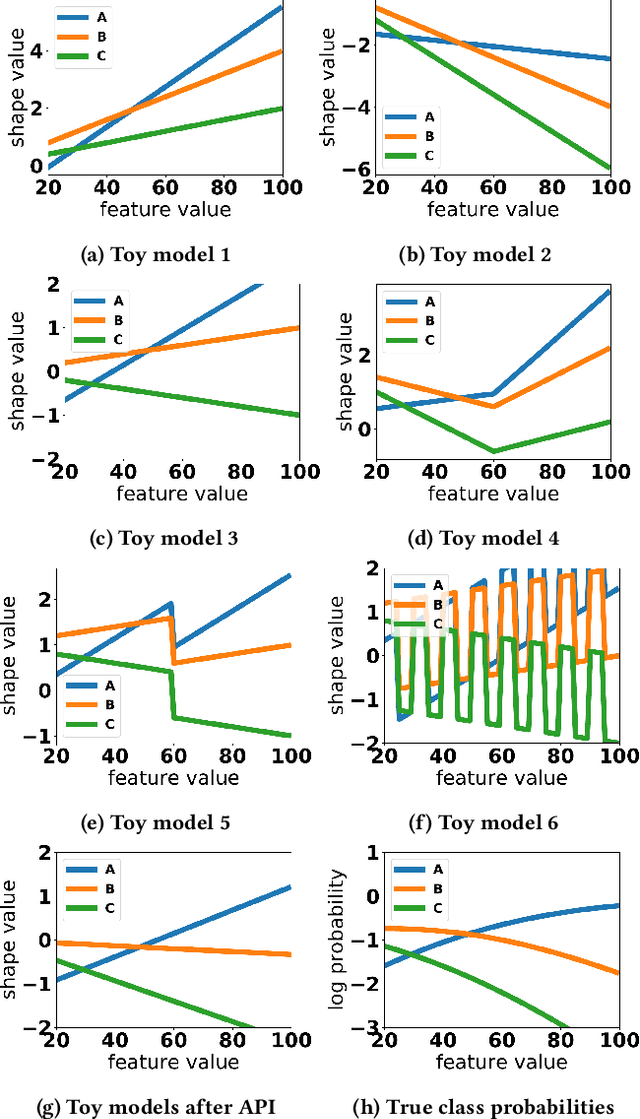
Generalized additive models (GAMs) are favored in many regression and binary classification problems because they are able to fit complex, nonlinear functions while still remaining interpretable. In the first part of this paper, we generalize a state-of-the-art GAM learning algorithm based on boosted trees to the multiclass setting, and show that this multiclass algorithm outperforms existing GAM fitting algorithms and sometimes matches the performance of full complex models. In the second part, we turn our attention to the interpretability of GAMs in the multiclass setting. Surprisingly, the natural interpretability of GAMs breaks down when there are more than two classes. Drawing inspiration from binary GAMs, we identify two axioms that any additive model must satisfy to not be visually misleading. We then develop a post-processing technique (API) that provably transforms pretrained additive models to satisfy the interpretability axioms without sacrificing accuracy. The technique works not just on models trained with our algorithm, but on any multiclass additive model. We demonstrate API on a 12-class infant-mortality dataset.

Defining Explanation in Probabilistic Systems

As probabilistic systems gain popularity and are coming into wider use, the need for a mechanism that explains the system's findings and recommendations becomes more critical. The system will also need a mechanism for ordering competing explanations. We examine two representative approaches to explanation in the literature - one due to G\"ardenfors and one due to Pearl - and show that both suffer from significant problems. We propose an approach to defining a notion of "better explanation" that combines some of the features of both together with more recent work by Pearl and others on causality.