Yin Lou
On Finding Bi-objective Pareto-optimal Fraud Prevention Rule Sets for Fintech Applications
Nov 02, 2023Abstract:Rules are widely used in Fintech institutions to make fraud prevention decisions, since rules are highly interpretable thanks to their intuitive if-then structure. In practice, a two-stage framework of fraud prevention decision rule set mining is usually employed in large Fintech institutions. This paper is concerned with finding high-quality rule subsets in a bi-objective space (such as precision and recall) from an initial pool of rules. To this end, we adopt the concept of Pareto optimality and aim to find a set of non-dominated rule subsets, which constitutes a Pareto front. We propose a heuristic-based framework called PORS and we identify that the core of PORS is the problem of solution selection on the front (SSF). We provide a systematic categorization of the SSF problem and a thorough empirical evaluation of various SSF methods on both public and proprietary datasets. We also introduce a novel variant of sequential covering algorithm called SpectralRules to encourage the diversity of the initial rule set and we empirically find that SpectralRules further improves the quality of the found Pareto front. On two real application scenarios within Alipay, we demonstrate the advantages of our proposed methodology compared to existing work.
Interpretability is Harder in the Multiclass Setting: Axiomatic Interpretability for Multiclass Additive Models
Oct 22, 2018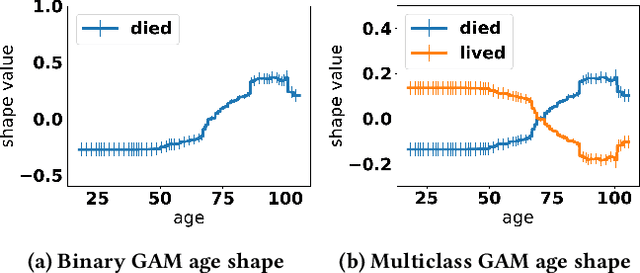
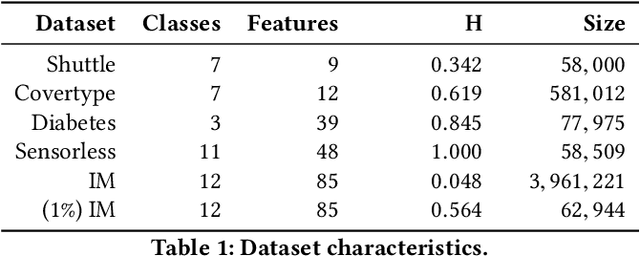
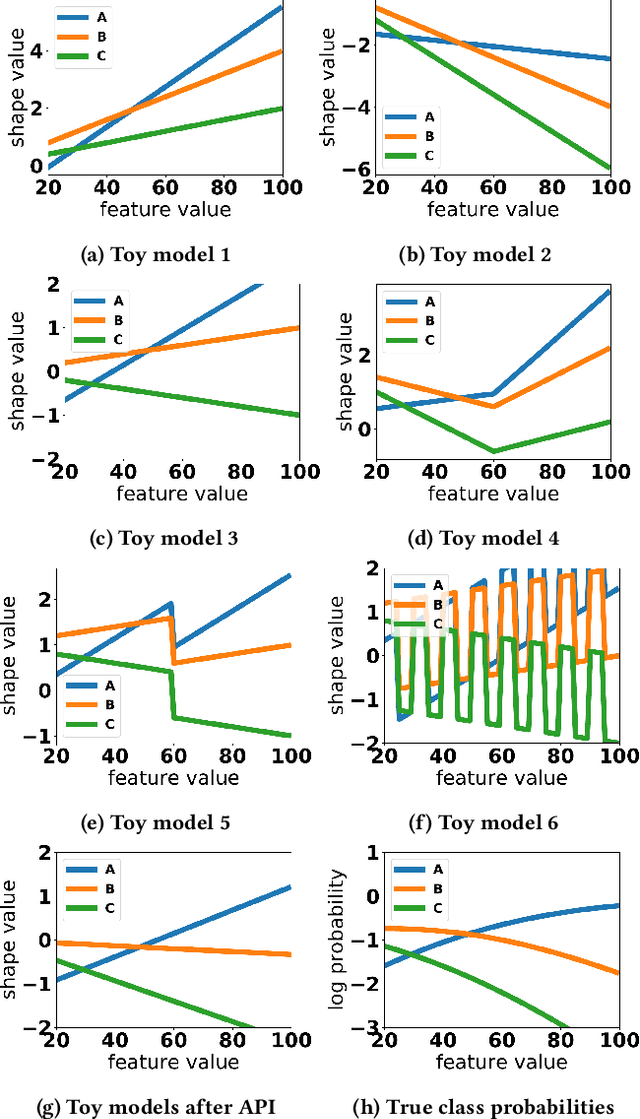
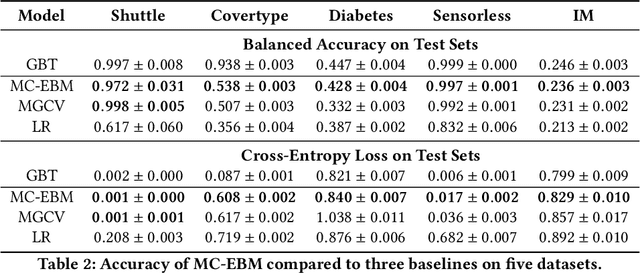
Abstract:Generalized additive models (GAMs) are favored in many regression and binary classification problems because they are able to fit complex, nonlinear functions while still remaining interpretable. In the first part of this paper, we generalize a state-of-the-art GAM learning algorithm based on boosted trees to the multiclass setting, and show that this multiclass algorithm outperforms existing GAM fitting algorithms and sometimes matches the performance of full complex models. In the second part, we turn our attention to the interpretability of GAMs in the multiclass setting. Surprisingly, the natural interpretability of GAMs breaks down when there are more than two classes. Drawing inspiration from binary GAMs, we identify two axioms that any additive model must satisfy to not be visually misleading. We then develop a post-processing technique (API) that provably transforms pretrained additive models to satisfy the interpretability axioms without sacrificing accuracy. The technique works not just on models trained with our algorithm, but on any multiclass additive model. We demonstrate API on a 12-class infant-mortality dataset.
Distill-and-Compare: Auditing Black-Box Models Using Transparent Model Distillation
Oct 11, 2018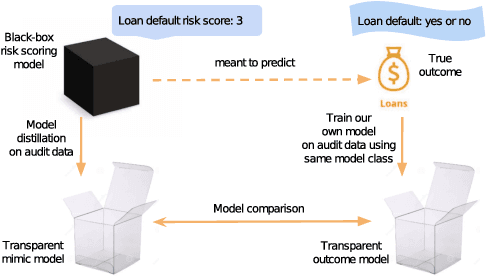

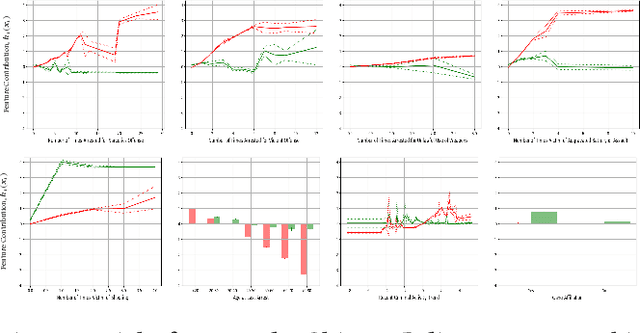
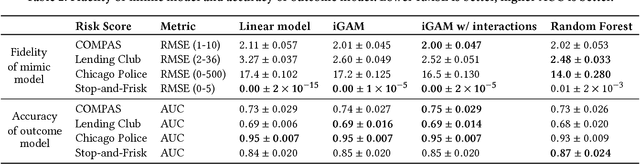
Abstract:Black-box risk scoring models permeate our lives, yet are typically proprietary or opaque. We propose Distill-and-Compare, a model distillation and comparison approach to audit such models. To gain insight into black-box models, we treat them as teachers, training transparent student models to mimic the risk scores assigned by black-box models. We compare the student model trained with distillation to a second un-distilled transparent model trained on ground-truth outcomes, and use differences between the two models to gain insight into the black-box model. Our approach can be applied in a realistic setting, without probing the black-box model API. We demonstrate the approach on four public data sets: COMPAS, Stop-and-Frisk, Chicago Police, and Lending Club. We also propose a statistical test to determine if a data set is missing key features used to train the black-box model. Our test finds that the ProPublica data is likely missing key feature(s) used in COMPAS.
Sparse Partially Linear Additive Models
Mar 27, 2018
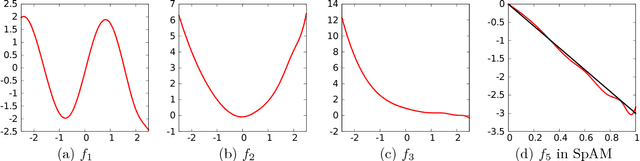
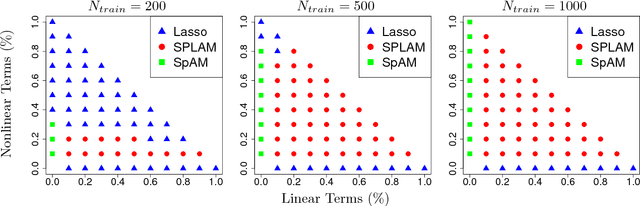

Abstract:The generalized partially linear additive model (GPLAM) is a flexible and interpretable approach to building predictive models. It combines features in an additive manner, allowing each to have either a linear or nonlinear effect on the response. However, the choice of which features to treat as linear or nonlinear is typically assumed known. Thus, to make a GPLAM a viable approach in situations in which little is known $a~priori$ about the features, one must overcome two primary model selection challenges: deciding which features to include in the model and determining which of these features to treat nonlinearly. We introduce the sparse partially linear additive model (SPLAM), which combines model fitting and $both$ of these model selection challenges into a single convex optimization problem. SPLAM provides a bridge between the lasso and sparse additive models. Through a statistical oracle inequality and thorough simulation, we demonstrate that SPLAM can outperform other methods across a broad spectrum of statistical regimes, including the high-dimensional ($p\gg N$) setting. We develop efficient algorithms that are applied to real data sets with half a million samples and over 45,000 features with excellent predictive performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge