Giles Hooker
Statistical Inference for Explainable Boosting Machines
Jan 26, 2026Abstract:Explainable boosting machines (EBMs) are popular "glass-box" models that learn a set of univariate functions using boosting trees. These achieve explainability through visualizations of each feature's effect. However, unlike linear model coefficients, uncertainty quantification for the learned univariate functions requires computationally intensive bootstrapping, making it hard to know which features truly matter. We provide an alternative using recent advances in statistical inference for gradient boosting, deriving methods for statistical inference as well as end-to-end theoretical guarantees. Using a moving average instead of a sum of trees (Boulevard regularization) allows the boosting process to converge to a feature-wise kernel ridge regression. This produces asymptotically normal predictions that achieve the minimax-optimal mean squared error for fitting Lipschitz GAMs with $p$ features at rate $O(pn^{-2/3})$, successfully avoiding the curse of dimensionality. We then construct prediction intervals for the response and confidence intervals for each learned univariate function with a runtime independent of the number of datapoints, enabling further explainability within EBMs.
Unifying Image Counterfactuals and Feature Attributions with Latent-Space Adversarial Attacks
Apr 21, 2025

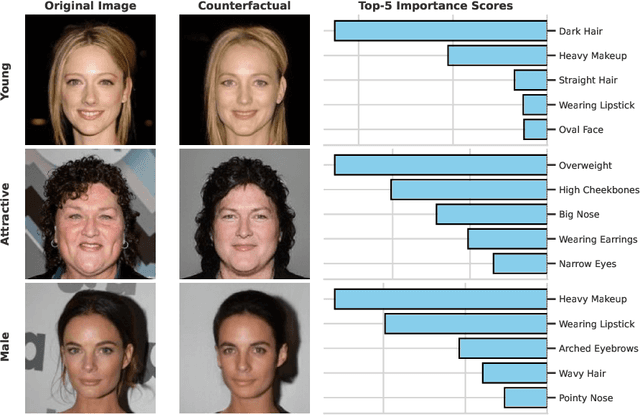
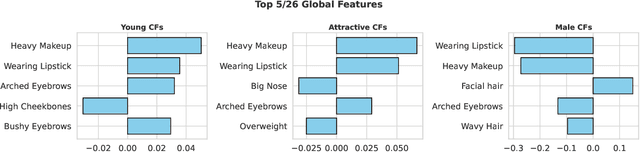
Abstract:Counterfactuals are a popular framework for interpreting machine learning predictions. These what if explanations are notoriously challenging to create for computer vision models: standard gradient-based methods are prone to produce adversarial examples, in which imperceptible modifications to image pixels provoke large changes in predictions. We introduce a new, easy-to-implement framework for counterfactual images that can flexibly adapt to contemporary advances in generative modeling. Our method, Counterfactual Attacks, resembles an adversarial attack on the representation of the image along a low-dimensional manifold. In addition, given an auxiliary dataset of image descriptors, we show how to accompany counterfactuals with feature attribution that quantify the changes between the original and counterfactual images. These importance scores can be aggregated into global counterfactual explanations that highlight the overall features driving model predictions. While this unification is possible for any counterfactual method, it has particular computational efficiency for ours. We demonstrate the efficacy of our approach with the MNIST and CelebA datasets.
Targeted Learning for Data Fairness
Feb 06, 2025Abstract:Data and algorithms have the potential to produce and perpetuate discrimination and disparate treatment. As such, significant effort has been invested in developing approaches to defining, detecting, and eliminating unfair outcomes in algorithms. In this paper, we focus on performing statistical inference for fairness. Prior work in fairness inference has largely focused on inferring the fairness properties of a given predictive algorithm. Here, we expand fairness inference by evaluating fairness in the data generating process itself, referred to here as data fairness. We perform inference on data fairness using targeted learning, a flexible framework for nonparametric inference. We derive estimators demographic parity, equal opportunity, and conditional mutual information. Additionally, we find that our estimators for probabilistic metrics exploit double robustness. To validate our approach, we perform several simulations and apply our estimators to real data.
Targeted Maximum Likelihood Estimation for Integral Projection Models in Population Ecology
Nov 12, 2024Abstract:Integral projection models (IPMs) are widely used to study population growth and the dynamics of demographic structure (e.g. age and size distributions) within a population.These models use data on individuals' growth, survival, and reproduction to predict changes in the population from one time point to the next and use these in turn to ask about long-term growth rates, the sensitivity of that growth rate to environmental factors, and aspects of the long term population such as how much reproduction concentrates in a few individuals; these quantities are not directly measurable from data and must be inferred from the model. Building IPMs requires us to develop models for individual fates over the next time step -- Did they survive? How much did they grow or shrink? Did they Reproduce? -- conditional on their initial state as well as on environmental covariates in a manner that accounts for the unobservable quantities that are are ultimately interested in estimating.Targeted maximum likelihood estimation (TMLE) methods are particularly well-suited to a framework in which we are largely interested in the consequences of models. These build machine learning-based models that estimate the probability distribution of the data we observe and define a target of inference as a function of these. The initial estimate for the distribution is then modified by tilting in the direction of the efficient influence function to both de-bias the parameter estimate and provide more accurate inference. In this paper, we employ TMLE to develop robust and efficient estimators for properties derived from a fitted IPM. Mathematically, we derive the efficient influence function and formulate the paths for the least favorable sub-models. Empirically, we conduct extensive simulations using real data from both long term studies of Idaho steppe plant communities and experimental Rotifer populations.
Targeted Learning for Variable Importance
Nov 04, 2024Abstract:Variable importance is one of the most widely used measures for interpreting machine learning with significant interest from both statistics and machine learning communities. Recently, increasing attention has been directed toward uncertainty quantification in these metrics. Current approaches largely rely on one-step procedures, which, while asymptotically efficient, can present higher sensitivity and instability in finite sample settings. To address these limitations, we propose a novel method by employing the targeted learning (TL) framework, designed to enhance robustness in inference for variable importance metrics. Our approach is particularly suited for conditional permutation variable importance. We show that it (i) retains the asymptotic efficiency of traditional methods, (ii) maintains comparable computational complexity, and (iii) delivers improved accuracy, especially in finite sample contexts. We further support these findings with numerical experiments that illustrate the practical advantages of our method and validate the theoretical results.
Accelerated Inference for Partially Observed Markov Processes using Automatic Differentiation
Jul 03, 2024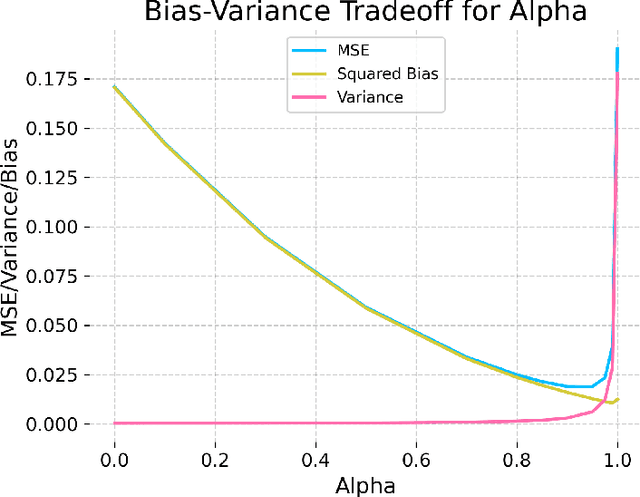

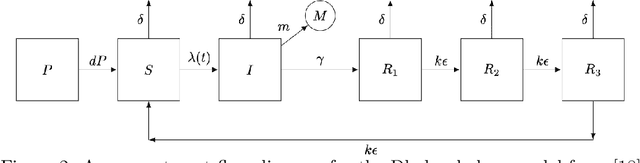
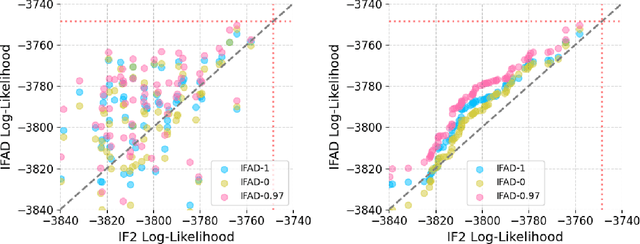
Abstract:Automatic differentiation (AD) has driven recent advances in machine learning, including deep neural networks and Hamiltonian Markov Chain Monte Carlo methods. Partially observed nonlinear stochastic dynamical systems have proved resistant to AD techniques because widely used particle filter algorithms yield an estimated likelihood function that is discontinuous as a function of the model parameters. We show how to embed two existing AD particle filter methods in a theoretical framework that provides an extension to a new class of algorithms. This new class permits a bias/variance tradeoff and hence a mean squared error substantially lower than the existing algorithms. We develop likelihood maximization algorithms suited to the Monte Carlo properties of the AD gradient estimate. Our algorithms require only a differentiable simulator for the latent dynamic system; by contrast, most previous approaches to AD likelihood maximization for particle filters require access to the system's transition probabilities. Numerical results indicate that a hybrid algorithm that uses AD to refine a coarse solution from an iterated filtering algorithm show substantial improvement on current state-of-the-art methods for a challenging scientific benchmark problem.
Differentiable Programming for Differential Equations: A Review
Jun 14, 2024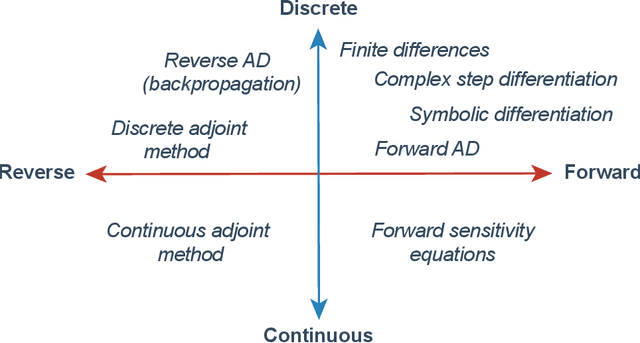
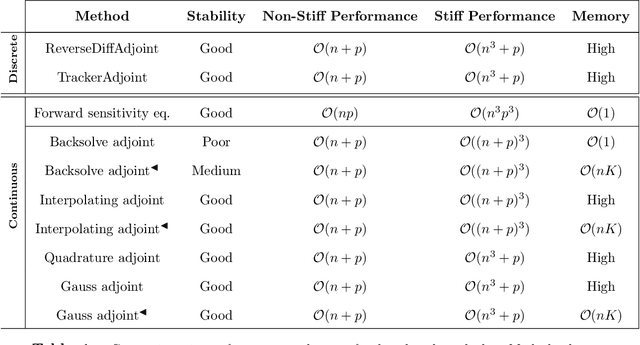
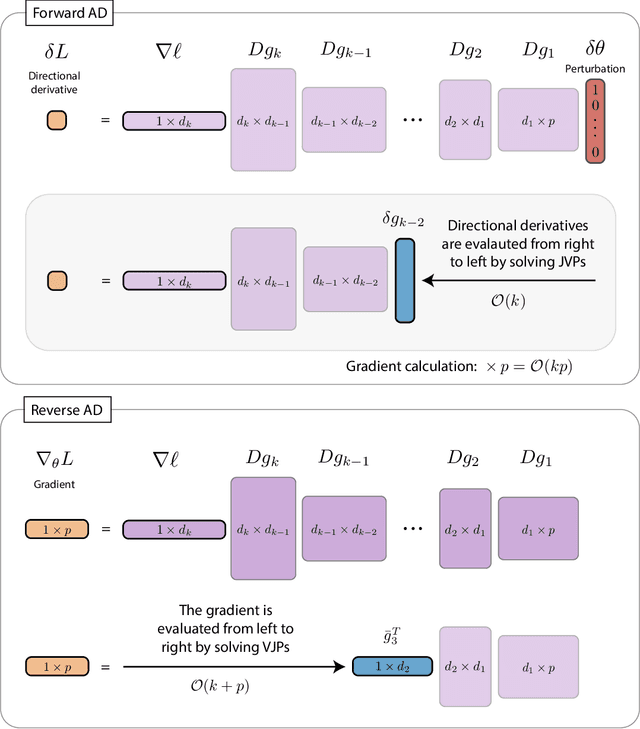
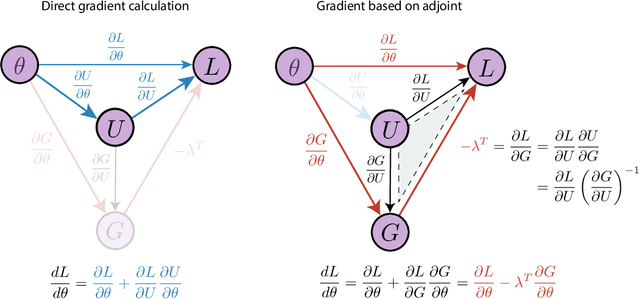
Abstract:The differentiable programming paradigm is a cornerstone of modern scientific computing. It refers to numerical methods for computing the gradient of a numerical model's output. Many scientific models are based on differential equations, where differentiable programming plays a crucial role in calculating model sensitivities, inverting model parameters, and training hybrid models that combine differential equations with data-driven approaches. Furthermore, recognizing the strong synergies between inverse methods and machine learning offers the opportunity to establish a coherent framework applicable to both fields. Differentiating functions based on the numerical solution of differential equations is non-trivial. Numerous methods based on a wide variety of paradigms have been proposed in the literature, each with pros and cons specific to the type of problem investigated. Here, we provide a comprehensive review of existing techniques to compute derivatives of numerical solutions of differential equations. We first discuss the importance of gradients of solutions of differential equations in a variety of scientific domains. Second, we lay out the mathematical foundations of the various approaches and compare them with each other. Third, we cover the computational considerations and explore the solutions available in modern scientific software. Last but not least, we provide best-practices and recommendations for practitioners. We hope that this work accelerates the fusion of scientific models and data, and fosters a modern approach to scientific modelling.
Why You Should Not Trust Interpretations in Machine Learning: Adversarial Attacks on Partial Dependence Plots
May 01, 2024Abstract:The adoption of artificial intelligence (AI) across industries has led to the widespread use of complex black-box models and interpretation tools for decision making. This paper proposes an adversarial framework to uncover the vulnerability of permutation-based interpretation methods for machine learning tasks, with a particular focus on partial dependence (PD) plots. This adversarial framework modifies the original black box model to manipulate its predictions for instances in the extrapolation domain. As a result, it produces deceptive PD plots that can conceal discriminatory behaviors while preserving most of the original model's predictions. This framework can produce multiple fooled PD plots via a single model. By using real-world datasets including an auto insurance claims dataset and COMPAS (Correctional Offender Management Profiling for Alternative Sanctions) dataset, our results show that it is possible to intentionally hide the discriminatory behavior of a predictor and make the black-box model appear neutral through interpretation tools like PD plots while retaining almost all the predictions of the original black-box model. Managerial insights for regulators and practitioners are provided based on the findings.
Longitudinal Counterfactuals: Constraints and Opportunities
Feb 29, 2024Abstract:Counterfactual explanations are a common approach to providing recourse to data subjects. However, current methodology can produce counterfactuals that cannot be achieved by the subject, making the use of counterfactuals for recourse difficult to justify in practice. Though there is agreement that plausibility is an important quality when using counterfactuals for algorithmic recourse, ground truth plausibility continues to be difficult to quantify. In this paper, we propose using longitudinal data to assess and improve plausibility in counterfactuals. In particular, we develop a metric that compares longitudinal differences to counterfactual differences, allowing us to evaluate how similar a counterfactual is to prior observed changes. Furthermore, we use this metric to generate plausible counterfactuals. Finally, we discuss some of the inherent difficulties of using counterfactuals for recourse.
Provably Stable Feature Rankings with SHAP and LIME
Jan 28, 2024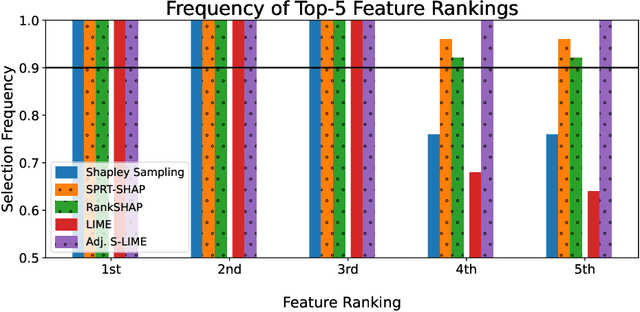
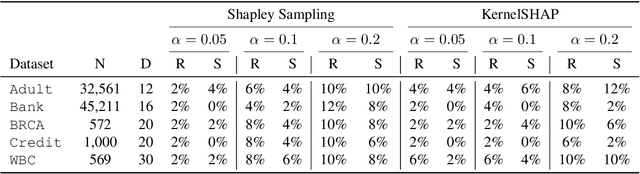
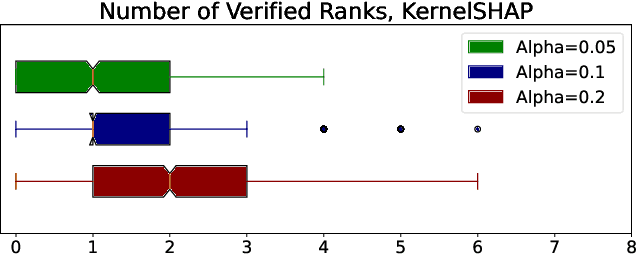
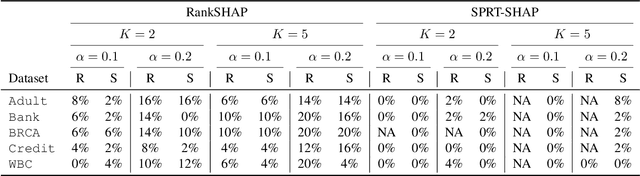
Abstract:Feature attributions are ubiquitous tools for understanding the predictions of machine learning models. However, popular methods for scoring input variables such as SHAP and LIME suffer from high instability due to random sampling. Leveraging ideas from multiple hypothesis testing, we devise attribution methods that correctly rank the most important features with high probability. Our algorithm RankSHAP guarantees that the $K$ highest Shapley values have the proper ordering with probability exceeding $1-\alpha$. Empirical results demonstrate its validity and impressive computational efficiency. We also build on previous work to yield similar results for LIME, ensuring the most important features are selected in the right order.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge