Accelerated Inference for Partially Observed Markov Processes using Automatic Differentiation

Automatic differentiation (AD) has driven recent advances in machine learning, including deep neural networks and Hamiltonian Markov Chain Monte Carlo methods. Partially observed nonlinear stochastic dynamical systems have proved resistant to AD techniques because widely used particle filter algorithms yield an estimated likelihood function that is discontinuous as a function of the model parameters. We show how to embed two existing AD particle filter methods in a theoretical framework that provides an extension to a new class of algorithms. This new class permits a bias/variance tradeoff and hence a mean squared error substantially lower than the existing algorithms. We develop likelihood maximization algorithms suited to the Monte Carlo properties of the AD gradient estimate. Our algorithms require only a differentiable simulator for the latent dynamic system; by contrast, most previous approaches to AD likelihood maximization for particle filters require access to the system's transition probabilities. Numerical results indicate that a hybrid algorithm that uses AD to refine a coarse solution from an iterated filtering algorithm show substantial improvement on current state-of-the-art methods for a challenging scientific benchmark problem.

Iterated Block Particle Filter for High-dimensional Parameter Learning: Beating the Curse of Dimensionality

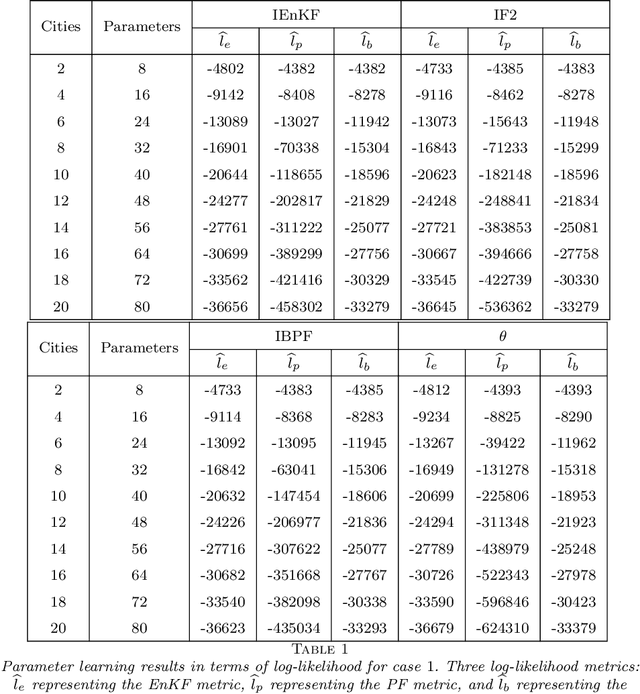
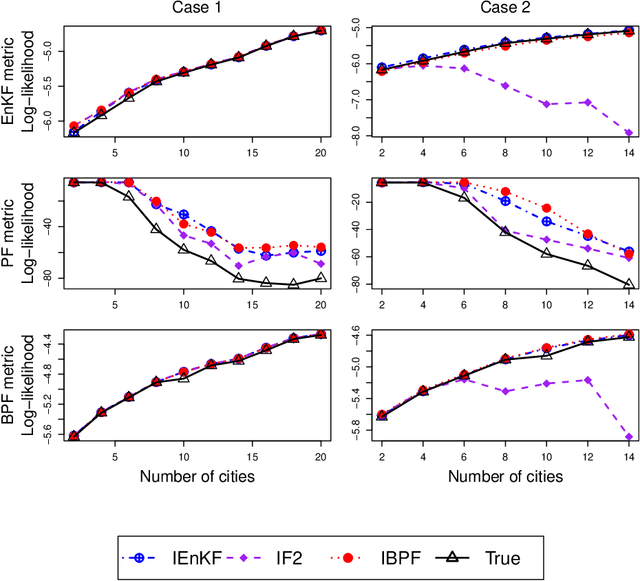
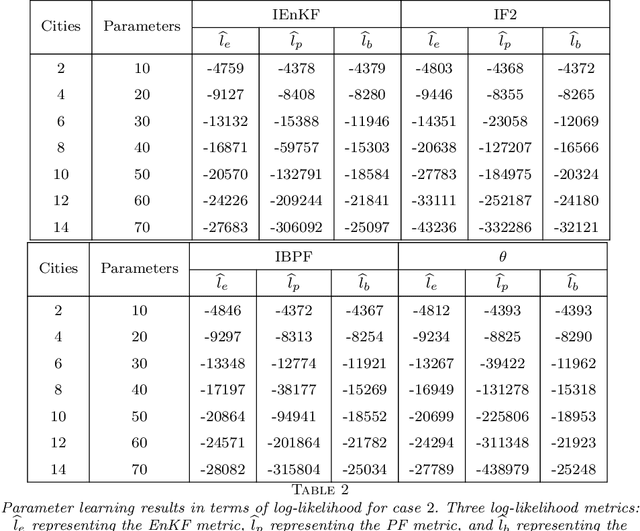
Parameter learning for high-dimensional, partially observed, and nonlinear stochastic processes is a methodological challenge. Spatiotemporal disease transmission systems provide examples of such processes giving rise to open inference problems. We propose the iterated block particle filter (IBPF) algorithm for learning high-dimensional parameters over graphical state space models with general state spaces, measures, transition densities and graph structure. Theoretical performance guarantees are obtained on beating the curse of dimensionality (COD), algorithm convergence, and likelihood maximization. Experiments on a highly nonlinear and non-Gaussian spatiotemporal model for measles transmission reveal that the iterated ensemble Kalman filter algorithm (Li et al. (2020)) is ineffective and the iterated filtering algorithm (Ionides et al. (2015)) suffers from the COD, while our IBPF algorithm beats COD consistently across various experiments with different metrics.