A&B BNN: Add&Bit-Operation-Only Hardware-Friendly Binary Neural Network

Binary neural networks utilize 1-bit quantized weights and activations to reduce both the model's storage demands and computational burden. However, advanced binary architectures still incorporate millions of inefficient and nonhardware-friendly full-precision multiplication operations. A&B BNN is proposed to directly remove part of the multiplication operations in a traditional BNN and replace the rest with an equal number of bit operations, introducing the mask layer and the quantized RPReLU structure based on the normalizer-free network architecture. The mask layer can be removed during inference by leveraging the intrinsic characteristics of BNN with straightforward mathematical transformations to avoid the associated multiplication operations. The quantized RPReLU structure enables more efficient bit operations by constraining its slope to be integer powers of 2. Experimental results achieved 92.30%, 69.35%, and 66.89% on the CIFAR-10, CIFAR-100, and ImageNet datasets, respectively, which are competitive with the state-of-the-art. Ablation studies have verified the efficacy of the quantized RPReLU structure, leading to a 1.14% enhancement on the ImageNet compared to using a fixed slope RLeakyReLU. The proposed add&bit-operation-only BNN offers an innovative approach for hardware-friendly network architecture.

Convergence of Dirichlet Forms for MCMC Optimal Scaling with General Target Distributions on Large Graphs

Markov chain Monte Carlo (MCMC) algorithms have played a significant role in statistics, physics, machine learning and others, and they are the only known general and efficient approach for some high-dimensional problems. The Metropolis-Hastings (MH) algorithm as the most classical MCMC algorithm, has had a great influence on the development and practice of science and engineering. The behavior of the MH algorithm in high-dimensional problems is typically investigated through a weak convergence result of diffusion processes. In this paper, we introduce Mosco convergence of Dirichlet forms in analyzing the MH algorithm on large graphs, whose target distribution is the Gibbs measure that includes any probability measure satisfying a Markov property. The abstract and powerful theory of Dirichlet forms allows us to work directly and naturally on the infinite-dimensional space, and our notion of Mosco convergence allows Dirichlet forms associated with the MH Markov chains to lie on changing Hilbert spaces. Through the optimal scaling problem, we demonstrate the impressive strengths of the Dirichlet form approach over the standard diffusion approach.

Iterated Block Particle Filter for High-dimensional Parameter Learning: Beating the Curse of Dimensionality

Parameter learning for high-dimensional, partially observed, and nonlinear stochastic processes is a methodological challenge. Spatiotemporal disease transmission systems provide examples of such processes giving rise to open inference problems. We propose the iterated block particle filter (IBPF) algorithm for learning high-dimensional parameters over graphical state space models with general state spaces, measures, transition densities and graph structure. Theoretical performance guarantees are obtained on beating the curse of dimensionality (COD), algorithm convergence, and likelihood maximization. Experiments on a highly nonlinear and non-Gaussian spatiotemporal model for measles transmission reveal that the iterated ensemble Kalman filter algorithm (Li et al. (2020)) is ineffective and the iterated filtering algorithm (Ionides et al. (2015)) suffers from the COD, while our IBPF algorithm beats COD consistently across various experiments with different metrics.

The mbsts package: Multivariate Bayesian Structural Time Series Models in R

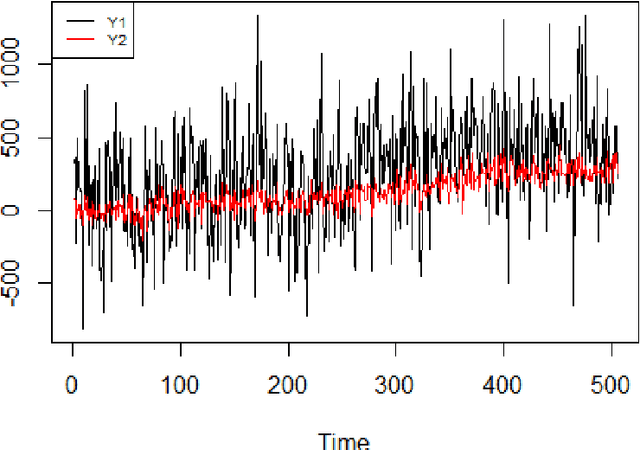
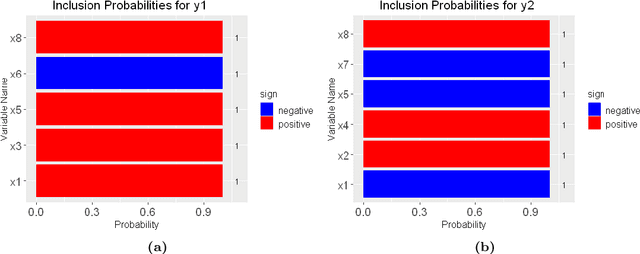
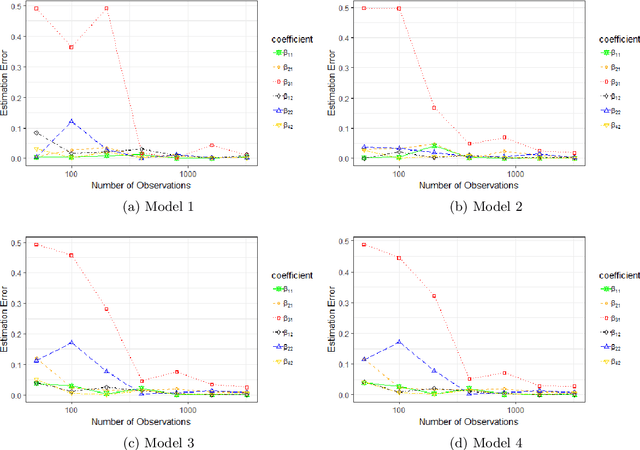
The multivariate Bayesian structural time series (MBSTS) model \citep{qiu2018multivariate,Jammalamadaka2019Predicting} as a generalized version of many structural time series models, deals with inference and prediction for multiple correlated time series, where one also has the choice of using a different candidate pool of contemporaneous predictors for each target series. The MBSTS model has wide applications and is ideal for feature selection, time series forecasting, nowcasting, inferring causal impact, and others. This paper demonstrates how to use the R package \pkg{mbsts} for MBSTS modeling, establishing a bridge between user-friendly and developer-friendly functions in package and the corresponding methodology. A simulated dataset and object-oriented functions in the \pkg{mbsts} package are explained in the way that enables users to flexibly add or deduct some components, as well as to simplify or complicate some settings.

Multivariate Quantile Bayesian Structural Time Series (MQBSTS) Model

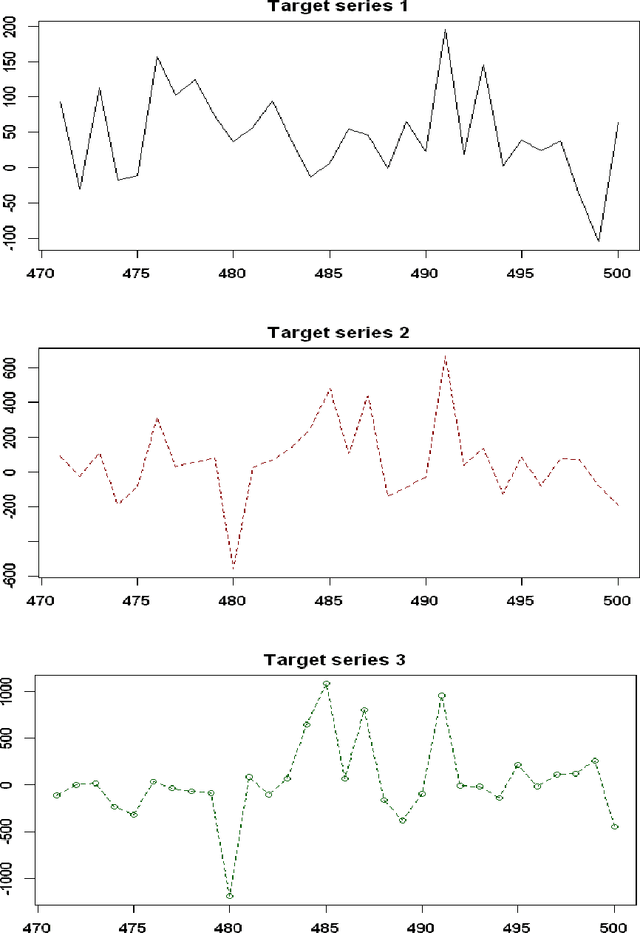
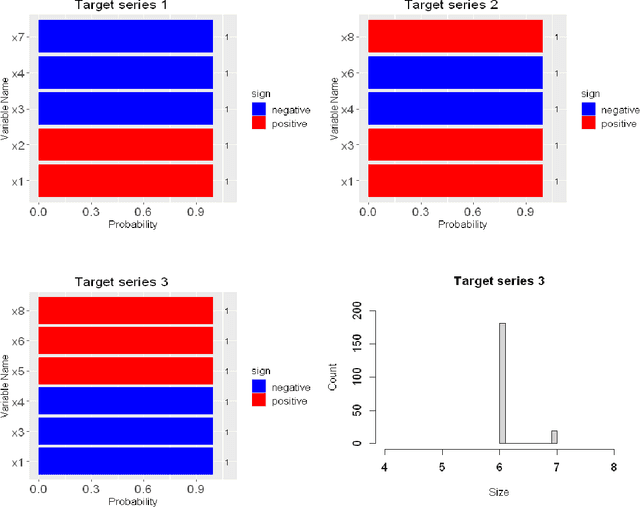
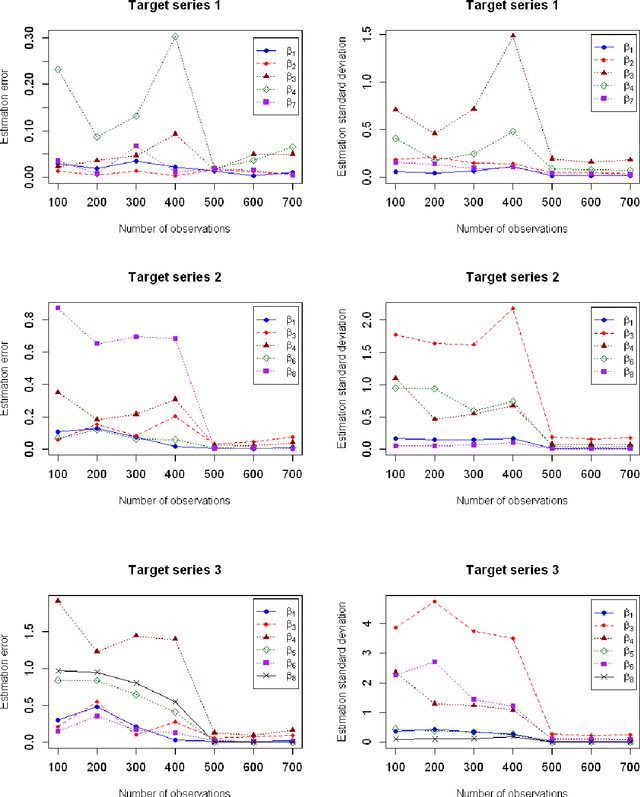
In this paper, we propose the multivariate quantile Bayesian structural time series (MQBSTS) model for the joint quantile time series forecast, which is the first such model for correlated multivariate time series to the author's best knowledge. The MQBSTS model also enables quantile based feature selection in its regression component where each time series has its own pool of contemporaneous external time series predictors, which is the first time that a fully data-driven quantile feature selection technique applicable to time series data to the author's best knowledge. Different from most machine learning algorithms, the MQBSTS model has very few hyper-parameters to tune, requires small datasets to train, converges fast, and is executable on ordinary personal computers. Extensive examinations on simulated data and empirical data confirmed that the MQBSTS model has superior performance in feature selection, parameter estimation, and forecast.

Facial Makeup Transfer Combining Illumination Transfer

To meet the women appearance needs, we present a novel virtual experience approach of facial makeup transfer, developed into windows platform application software. The makeup effects could present on the user's input image in real time, with an only single reference image. The input image and reference image are divided into three layers by facial feature points landmarked: facial structure layer, facial color layer, and facial detail layer. Except for the above layers are processed by different algorithms to generate output image, we also add illumination transfer, so that the illumination effect of the reference image is automatically transferred to the input image. Our approach has the following three advantages: (1) Black or dark and white facial makeup could be effectively transferred by introducing illumination transfer; (2) Efficiently transfer facial makeup within seconds compared to those methods based on deep learning frameworks; (3) Reference images with the air-bangs could transfer makeup perfectly.

The non-tightness of the reconstruction threshold of a 4 states symmetric model with different in-block and out-block mutations

The tree reconstruction problem is to collect and analyze massive data at the $n$th level of the tree, to identify whether there is non-vanishing information of the root, as $n$ goes to infinity. Its connection to the clustering problem in the setting of the stochastic block model, which has wide applications in machine learning and data mining, has been well established. For the stochastic block model, an "information-theoretically-solvable-but-computationally-hard" region, or say "hybrid-hard phase", appears whenever the reconstruction bound is not tight of the corresponding reconstruction on the tree problem. Although it has been studied in numerous contexts, the existing literature with rigorous reconstruction thresholds established are very limited, and it becomes extremely challenging when the model under investigation has $4$ states (the stochastic block model with $4$ communities). In this paper, inspired by the newly proposed $q_1+q_2$ stochastic block model, we study a $4$ states symmetric model with different in-block and out-block transition probabilities, and rigorously give the conditions for the non-tightness of the reconstruction threshold.

Multivariate Bayesian Structural Time Series Model

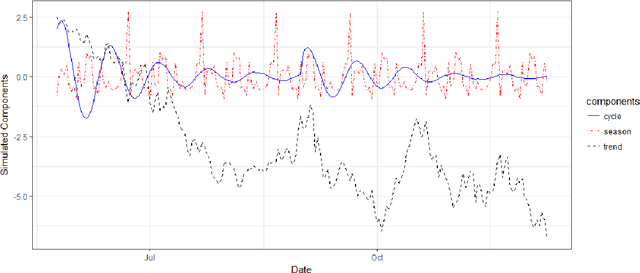
This paper deals with inference and prediction for multiple correlated time series, where one has also the choice of using a candidate pool of contemporaneous predictors for each target series. Starting with a structural model for the time-series, Bayesian tools are used for model fitting, prediction, and feature selection, thus extending some recent work along these lines for the univariate case. The Bayesian paradigm in this multivariate setting helps the model avoid overfitting as well as capture correlations among the multiple time series with the various state components. The model provides needed flexibility to choose a different set of components and available predictors for each target series. The cyclical component in the model can handle large variations in the short term, which may be caused by external shocks. We run extensive simulations to investigate properties such as estimation accuracy and performance in forecasting. We then run an empirical study with one-step-ahead prediction on the max log return of a portfolio of stocks that involve four leading financial institutions. Both the simulation studies and the extensive empirical study confirm that this multivariate model outperforms three other benchmark models, viz. a model that treats each target series as independent, the autoregressive integrated moving average model with regression (ARIMAX), and the multivariate ARIMAX (MARIMAX) model.