Class Machine Unlearning for Complex Data via Concepts Inference and Data Poisoning

In current AI era, users may request AI companies to delete their data from the training dataset due to the privacy concerns. As a model owner, retraining a model will consume significant computational resources. Therefore, machine unlearning is a new emerged technology to allow model owner to delete requested training data or a class with little affecting on the model performance. However, for large-scaling complex data, such as image or text data, unlearning a class from a model leads to a inferior performance due to the difficulty to identify the link between classes and model. An inaccurate class deleting may lead to over or under unlearning. In this paper, to accurately defining the unlearning class of complex data, we apply the definition of Concept, rather than an image feature or a token of text data, to represent the semantic information of unlearning class. This new representation can cut the link between the model and the class, leading to a complete erasing of the impact of a class. To analyze the impact of the concept of complex data, we adopt a Post-hoc Concept Bottleneck Model, and Integrated Gradients to precisely identify concepts across different classes. Next, we take advantage of data poisoning with random and targeted labels to propose unlearning methods. We test our methods on both image classification models and large language models (LLMs). The results consistently show that the proposed methods can accurately erase targeted information from models and can largely maintain the performance of the models.

GANDSE: Generative Adversarial Network based Design Space Exploration for Neural Network Accelerator Design

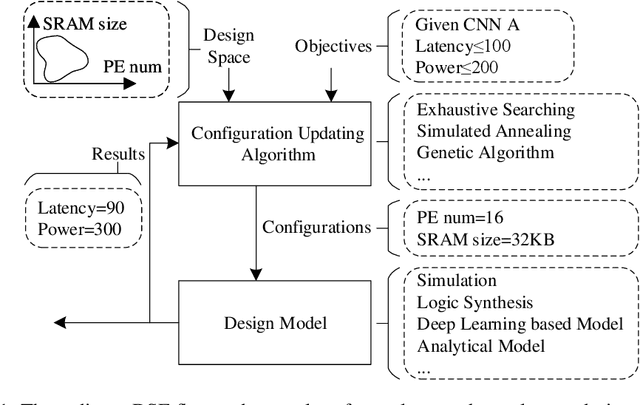
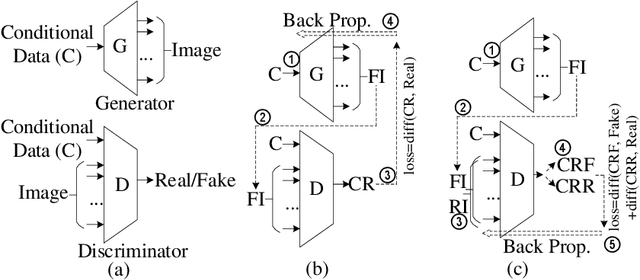
With the popularity of deep learning, the hardware implementation platform of deep learning has received increasing interest. Unlike the general purpose devices, e.g., CPU, or GPU, where the deep learning algorithms are executed at the software level, neural network hardware accelerators directly execute the algorithms to achieve higher both energy efficiency and performance improvements. However, as the deep learning algorithms evolve frequently, the engineering effort and cost of designing the hardware accelerators are greatly increased. To improve the design quality while saving the cost, design automation for neural network accelerators was proposed, where design space exploration algorithms are used to automatically search the optimized accelerator design within a design space. Nevertheless, the increasing complexity of the neural network accelerators brings the increasing dimensions to the design space. As a result, the previous design space exploration algorithms are no longer effective enough to find an optimized design. In this work, we propose a neural network accelerator design automation framework named GANDSE, where we rethink the problem of design space exploration, and propose a novel approach based on the generative adversarial network (GAN) to support an optimized exploration for high dimension large design space. The experiments show that GANDSE is able to find the more optimized designs in negligible time compared with approaches including multilayer perceptron and deep reinforcement learning.

The non-tightness of the reconstruction threshold of a 4 states symmetric model with different in-block and out-block mutations

The tree reconstruction problem is to collect and analyze massive data at the $n$th level of the tree, to identify whether there is non-vanishing information of the root, as $n$ goes to infinity. Its connection to the clustering problem in the setting of the stochastic block model, which has wide applications in machine learning and data mining, has been well established. For the stochastic block model, an "information-theoretically-solvable-but-computationally-hard" region, or say "hybrid-hard phase", appears whenever the reconstruction bound is not tight of the corresponding reconstruction on the tree problem. Although it has been studied in numerous contexts, the existing literature with rigorous reconstruction thresholds established are very limited, and it becomes extremely challenging when the model under investigation has $4$ states (the stochastic block model with $4$ communities). In this paper, inspired by the newly proposed $q_1+q_2$ stochastic block model, we study a $4$ states symmetric model with different in-block and out-block transition probabilities, and rigorously give the conditions for the non-tightness of the reconstruction threshold.