The mbsts package: Multivariate Bayesian Structural Time Series Models in R

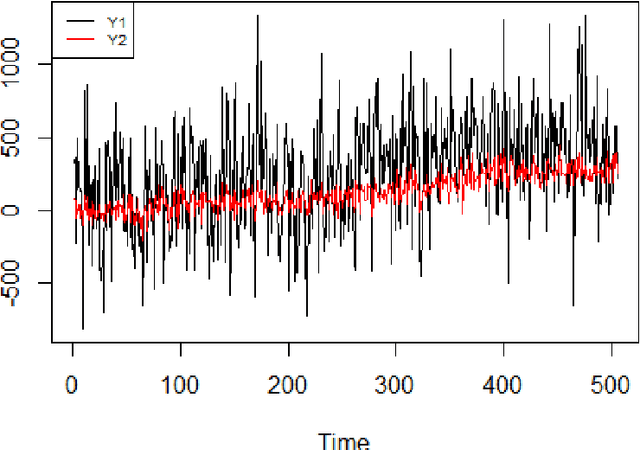
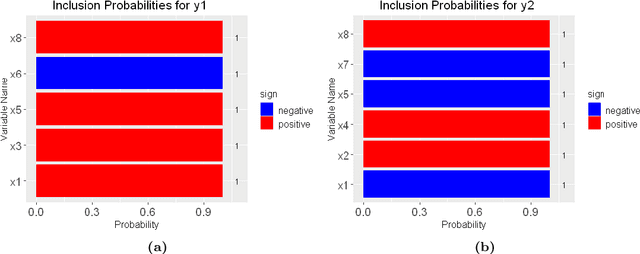
The multivariate Bayesian structural time series (MBSTS) model \citep{qiu2018multivariate,Jammalamadaka2019Predicting} as a generalized version of many structural time series models, deals with inference and prediction for multiple correlated time series, where one also has the choice of using a different candidate pool of contemporaneous predictors for each target series. The MBSTS model has wide applications and is ideal for feature selection, time series forecasting, nowcasting, inferring causal impact, and others. This paper demonstrates how to use the R package \pkg{mbsts} for MBSTS modeling, establishing a bridge between user-friendly and developer-friendly functions in package and the corresponding methodology. A simulated dataset and object-oriented functions in the \pkg{mbsts} package are explained in the way that enables users to flexibly add or deduct some components, as well as to simplify or complicate some settings.

Linear Iterative Feature Embedding: An Ensemble Framework for Interpretable Model

A new ensemble framework for interpretable model called Linear Iterative Feature Embedding (LIFE) has been developed to achieve high prediction accuracy, easy interpretation and efficient computation simultaneously. The LIFE algorithm is able to fit a wide single-hidden-layer neural network (NN) accurately with three steps: defining the subsets of a dataset by the linear projections of neural nodes, creating the features from multiple narrow single-hidden-layer NNs trained on the different subsets of the data, combining the features with a linear model. The theoretical rationale behind LIFE is also provided by the connection to the loss ambiguity decomposition of stack ensemble methods. Both simulation and empirical experiments confirm that LIFE consistently outperforms directly trained single-hidden-layer NNs and also outperforms many other benchmark models, including multi-layers Feed Forward Neural Network (FFNN), Xgboost, and Random Forest (RF) in many experiments. As a wide single-hidden-layer NN, LIFE is intrinsically interpretable. Meanwhile, both variable importance and global main and interaction effects can be easily created and visualized. In addition, the parallel nature of the base learner building makes LIFE computationally efficient by leveraging parallel computing.

Multivariate Bayesian Structural Time Series Model

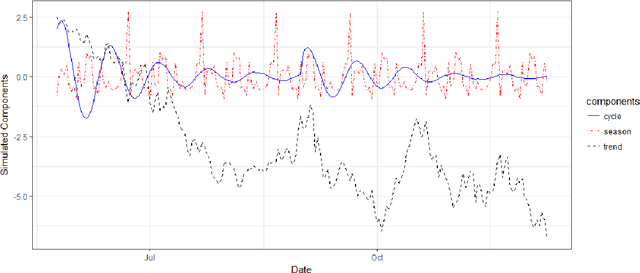
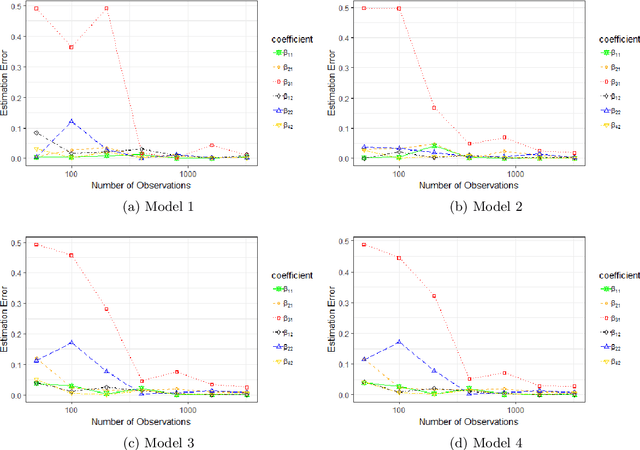
This paper deals with inference and prediction for multiple correlated time series, where one has also the choice of using a candidate pool of contemporaneous predictors for each target series. Starting with a structural model for the time-series, Bayesian tools are used for model fitting, prediction, and feature selection, thus extending some recent work along these lines for the univariate case. The Bayesian paradigm in this multivariate setting helps the model avoid overfitting as well as capture correlations among the multiple time series with the various state components. The model provides needed flexibility to choose a different set of components and available predictors for each target series. The cyclical component in the model can handle large variations in the short term, which may be caused by external shocks. We run extensive simulations to investigate properties such as estimation accuracy and performance in forecasting. We then run an empirical study with one-step-ahead prediction on the max log return of a portfolio of stocks that involve four leading financial institutions. Both the simulation studies and the extensive empirical study confirm that this multivariate model outperforms three other benchmark models, viz. a model that treats each target series as independent, the autoregressive integrated moving average model with regression (ARIMAX), and the multivariate ARIMAX (MARIMAX) model.