Differentiable Programming for Differential Equations: A Review

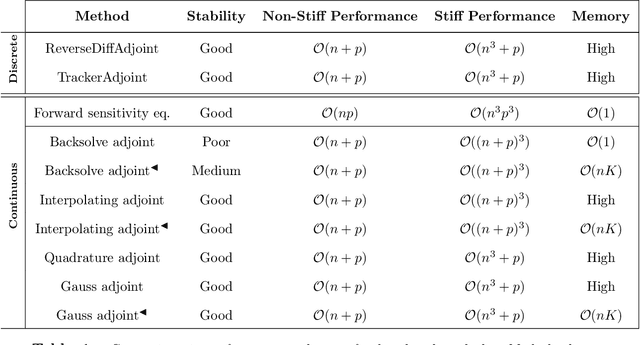
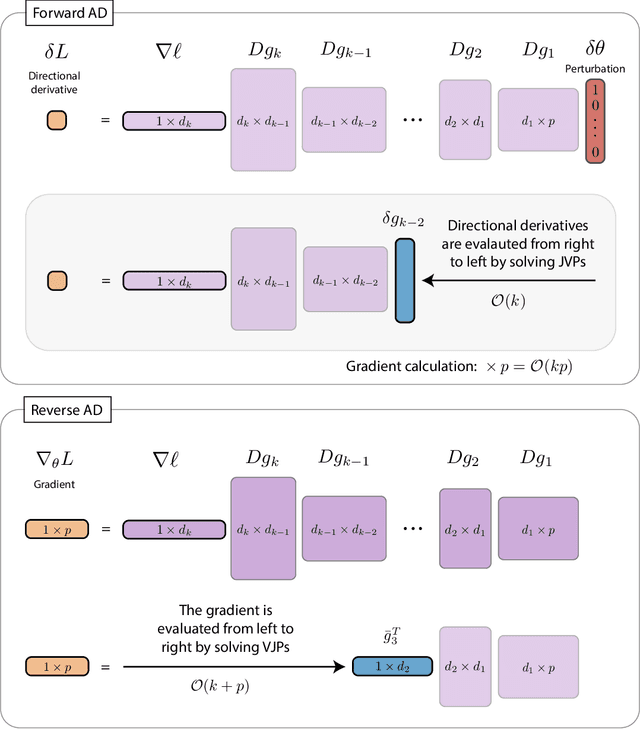
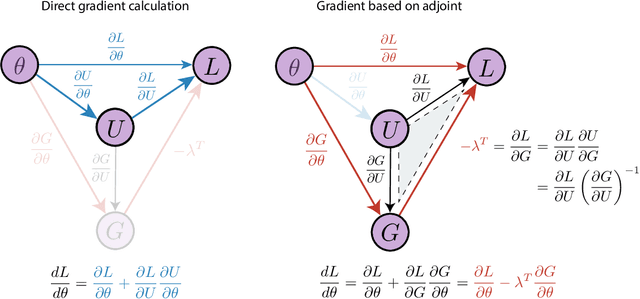
The differentiable programming paradigm is a cornerstone of modern scientific computing. It refers to numerical methods for computing the gradient of a numerical model's output. Many scientific models are based on differential equations, where differentiable programming plays a crucial role in calculating model sensitivities, inverting model parameters, and training hybrid models that combine differential equations with data-driven approaches. Furthermore, recognizing the strong synergies between inverse methods and machine learning offers the opportunity to establish a coherent framework applicable to both fields. Differentiating functions based on the numerical solution of differential equations is non-trivial. Numerous methods based on a wide variety of paradigms have been proposed in the literature, each with pros and cons specific to the type of problem investigated. Here, we provide a comprehensive review of existing techniques to compute derivatives of numerical solutions of differential equations. We first discuss the importance of gradients of solutions of differential equations in a variety of scientific domains. Second, we lay out the mathematical foundations of the various approaches and compare them with each other. Third, we cover the computational considerations and explore the solutions available in modern scientific software. Last but not least, we provide best-practices and recommendations for practitioners. We hope that this work accelerates the fusion of scientific models and data, and fosters a modern approach to scientific modelling.

A Concise Tiling Strategy for Preserving Spatial Context in Earth Observation Imagery

We propose a new tiling strategy, Flip-n-Slide, which has been developed for specific use with large Earth observation satellite images when the location of objects-of-interest (OoI) is unknown and spatial context can be necessary for class disambiguation. Flip-n-Slide is a concise and minimalistic approach that allows OoI to be represented at multiple tile positions and orientations. This strategy introduces multiple views of spatio-contextual information, without introducing redundancies into the training set. By maintaining distinct transformation permutations for each tile overlap, we enhance the generalizability of the training set without misrepresenting the true data distribution. Our experiments validate the effectiveness of Flip-n-Slide in the task of semantic segmentation, a necessary data product in geophysical studies. We find that Flip-n-Slide outperforms the previous state-of-the-art augmentation routines for tiled data in all evaluation metrics. For underrepresented classes, Flip-n-Slide increases precision by as much as 15.8%.