Differentiable Programming for Differential Equations: A Review
Paper and Code
Jun 14, 2024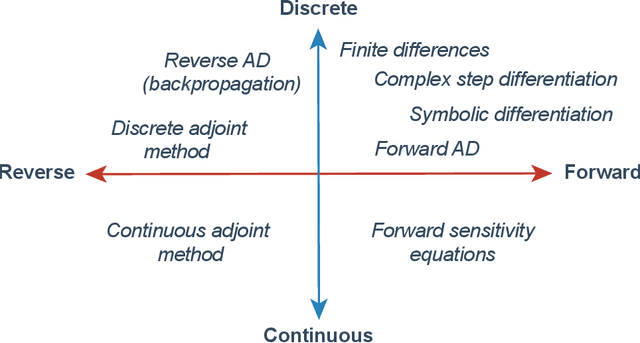
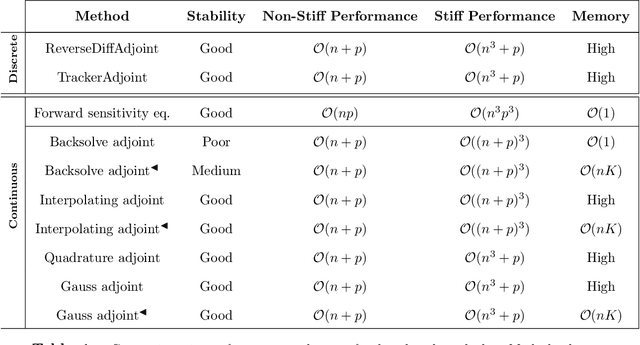
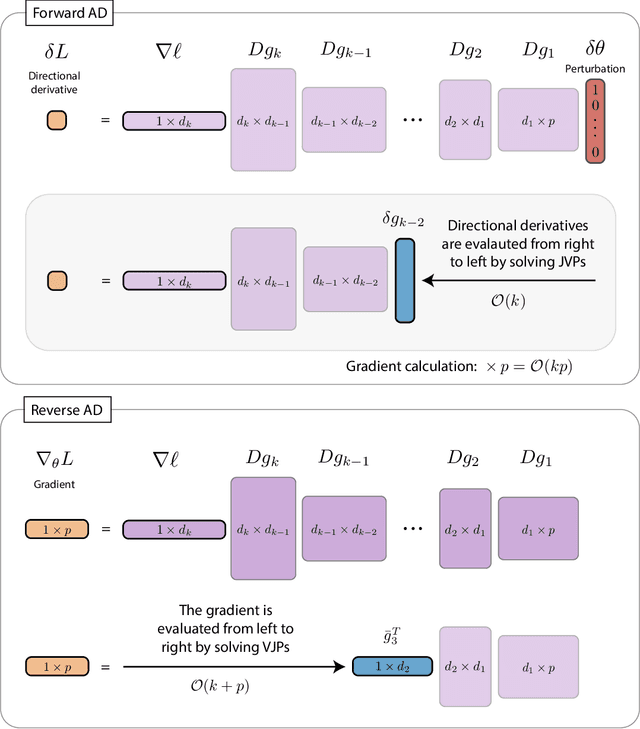
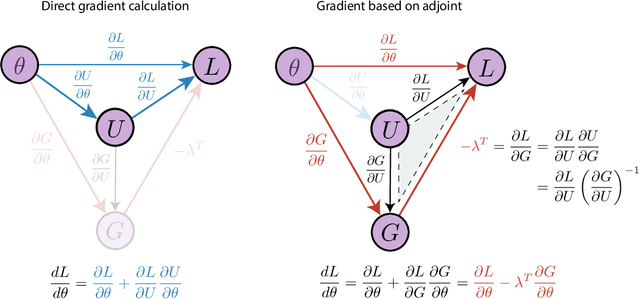
The differentiable programming paradigm is a cornerstone of modern scientific computing. It refers to numerical methods for computing the gradient of a numerical model's output. Many scientific models are based on differential equations, where differentiable programming plays a crucial role in calculating model sensitivities, inverting model parameters, and training hybrid models that combine differential equations with data-driven approaches. Furthermore, recognizing the strong synergies between inverse methods and machine learning offers the opportunity to establish a coherent framework applicable to both fields. Differentiating functions based on the numerical solution of differential equations is non-trivial. Numerous methods based on a wide variety of paradigms have been proposed in the literature, each with pros and cons specific to the type of problem investigated. Here, we provide a comprehensive review of existing techniques to compute derivatives of numerical solutions of differential equations. We first discuss the importance of gradients of solutions of differential equations in a variety of scientific domains. Second, we lay out the mathematical foundations of the various approaches and compare them with each other. Third, we cover the computational considerations and explore the solutions available in modern scientific software. Last but not least, we provide best-practices and recommendations for practitioners. We hope that this work accelerates the fusion of scientific models and data, and fosters a modern approach to scientific modelling.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge