Differentiable Programming for Differential Equations: A Review

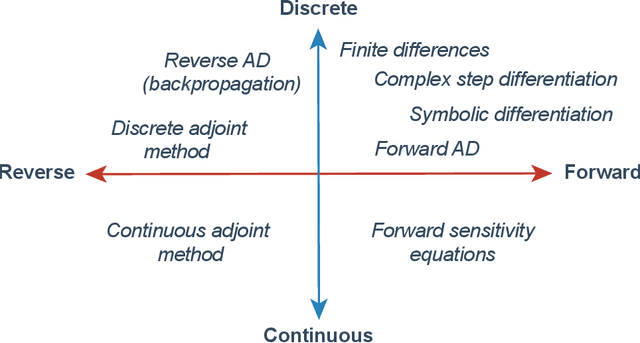
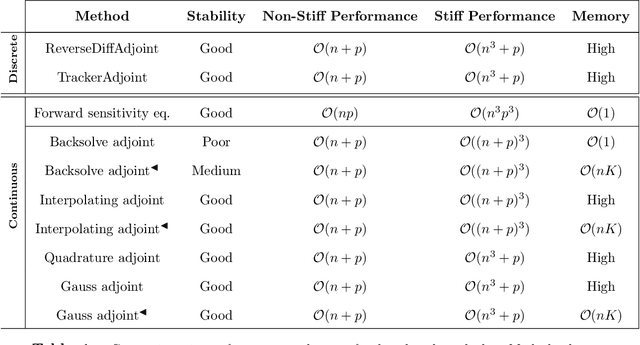
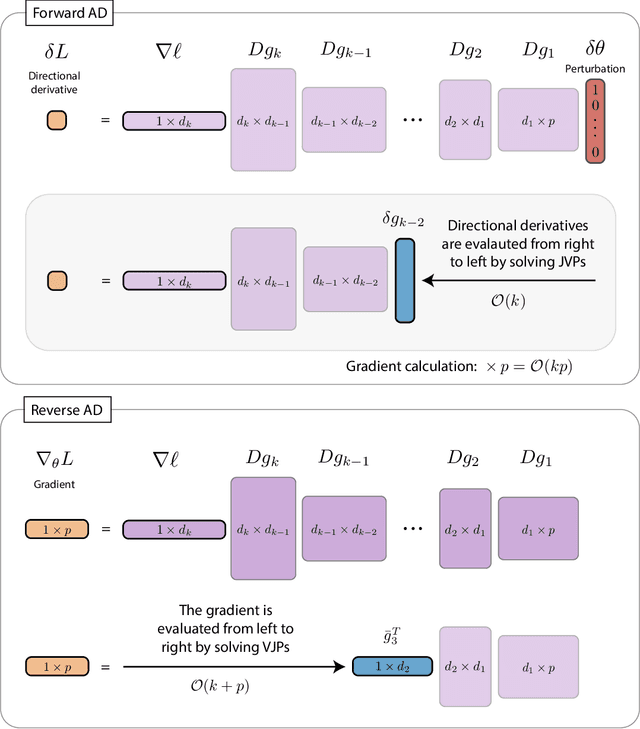
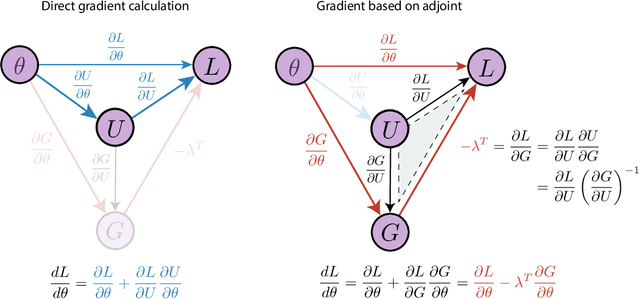
The differentiable programming paradigm is a cornerstone of modern scientific computing. It refers to numerical methods for computing the gradient of a numerical model's output. Many scientific models are based on differential equations, where differentiable programming plays a crucial role in calculating model sensitivities, inverting model parameters, and training hybrid models that combine differential equations with data-driven approaches. Furthermore, recognizing the strong synergies between inverse methods and machine learning offers the opportunity to establish a coherent framework applicable to both fields. Differentiating functions based on the numerical solution of differential equations is non-trivial. Numerous methods based on a wide variety of paradigms have been proposed in the literature, each with pros and cons specific to the type of problem investigated. Here, we provide a comprehensive review of existing techniques to compute derivatives of numerical solutions of differential equations. We first discuss the importance of gradients of solutions of differential equations in a variety of scientific domains. Second, we lay out the mathematical foundations of the various approaches and compare them with each other. Third, we cover the computational considerations and explore the solutions available in modern scientific software. Last but not least, we provide best-practices and recommendations for practitioners. We hope that this work accelerates the fusion of scientific models and data, and fosters a modern approach to scientific modelling.

ClimAlign: Unsupervised statistical downscaling of climate variables via normalizing flows

Downscaling is a landmark task in climate science and meteorology in which the goal is to use coarse scale, spatio-temporal data to infer values at finer scales. Statistical downscaling aims to approximate this task using statistical patterns gleaned from an existing dataset of downscaled values, often obtained from observations or physical models. In this work, we investigate the application of deep latent variable learning to the task of statistical downscaling. We present ClimAlign, a novel method for unsupervised, generative downscaling using adaptations of recent work in normalizing flows for variational inference. We evaluate the viability of our method using several different metrics on two datasets consisting of daily temperature and precipitation values gridded at low (1 degree latitude/longitude) and high (1/4 and 1/8 degree) resolutions. We show that our method achieves comparable predictive performance to existing supervised statistical downscaling methods while simultaneously allowing for both conditional and unconditional sampling from the joint distribution over high and low resolution spatial fields. We provide publicly accessible implementations of our method, as well as the baselines used for comparison, on GitHub.

Learning to Reason

Automated theorem proving has long been a key task of artificial intelligence. Proofs form the bedrock of rigorous scientific inquiry. Many tools for both partially and fully automating their derivations have been developed over the last half a century. Some examples of state-of-the-art provers are E (Schulz, 2013), VAMPIRE (Kov\'acs & Voronkov, 2013), and Prover9 (McCune, 2005-2010). Newer theorem provers, such as E, use superposition calculus in place of more traditional resolution and tableau based methods. There have also been a number of past attempts to apply machine learning methods to guiding proof search. Suttner & Ertel proposed a multilayer-perceptron based method using hand-engineered features as far back as 1990; Urban et al (2011) apply machine learning to tableau calculus; and Loos et al (2017) recently proposed a method for guiding the E theorem prover using deep nerual networks. All of this prior work, however, has one common limitation: they all rely on the axioms of classical first-order logic. Very little attention has been paid to automated theorem proving for non-classical logics. One of the only recent examples is McLaughlin & Pfenning (2008) who applied the polarized inverse method to intuitionistic propositional logic. The literature is otherwise mostly silent. This is truly unfortunate, as there are many reasons to desire non-classical proofs over classical. Constructive/intuitionistic proofs should be of particular interest to computer scientists thanks to the well-known Curry-Howard correspondence (Howard, 1980) which tells us that all terminating programs correspond to a proof in intuitionistic logic and vice versa. This work explores using Q-learning (Watkins, 1989) to inform proof search for a specific system called non-classical logic called Core Logic (Tennant, 2017).