Targeted Maximum Likelihood Estimation for Integral Projection Models in Population Ecology

Integral projection models (IPMs) are widely used to study population growth and the dynamics of demographic structure (e.g. age and size distributions) within a population.These models use data on individuals' growth, survival, and reproduction to predict changes in the population from one time point to the next and use these in turn to ask about long-term growth rates, the sensitivity of that growth rate to environmental factors, and aspects of the long term population such as how much reproduction concentrates in a few individuals; these quantities are not directly measurable from data and must be inferred from the model. Building IPMs requires us to develop models for individual fates over the next time step -- Did they survive? How much did they grow or shrink? Did they Reproduce? -- conditional on their initial state as well as on environmental covariates in a manner that accounts for the unobservable quantities that are are ultimately interested in estimating.Targeted maximum likelihood estimation (TMLE) methods are particularly well-suited to a framework in which we are largely interested in the consequences of models. These build machine learning-based models that estimate the probability distribution of the data we observe and define a target of inference as a function of these. The initial estimate for the distribution is then modified by tilting in the direction of the efficient influence function to both de-bias the parameter estimate and provide more accurate inference. In this paper, we employ TMLE to develop robust and efficient estimators for properties derived from a fitted IPM. Mathematically, we derive the efficient influence function and formulate the paths for the least favorable sub-models. Empirically, we conduct extensive simulations using real data from both long term studies of Idaho steppe plant communities and experimental Rotifer populations.

Targeted Learning for Variable Importance

Variable importance is one of the most widely used measures for interpreting machine learning with significant interest from both statistics and machine learning communities. Recently, increasing attention has been directed toward uncertainty quantification in these metrics. Current approaches largely rely on one-step procedures, which, while asymptotically efficient, can present higher sensitivity and instability in finite sample settings. To address these limitations, we propose a novel method by employing the targeted learning (TL) framework, designed to enhance robustness in inference for variable importance metrics. Our approach is particularly suited for conditional permutation variable importance. We show that it (i) retains the asymptotic efficiency of traditional methods, (ii) maintains comparable computational complexity, and (iii) delivers improved accuracy, especially in finite sample contexts. We further support these findings with numerical experiments that illustrate the practical advantages of our method and validate the theoretical results.

Testing for the Markov Property in Time Series via Deep Conditional Generative Learning

The Markov property is widely imposed in analysis of time series data. Correspondingly, testing the Markov property, and relatedly, inferring the order of a Markov model, are of paramount importance. In this article, we propose a nonparametric test for the Markov property in high-dimensional time series via deep conditional generative learning. We also apply the test sequentially to determine the order of the Markov model. We show that the test controls the type-I error asymptotically, and has the power approaching one. Our proposal makes novel contributions in several ways. We utilize and extend state-of-the-art deep generative learning to estimate the conditional density functions, and establish a sharp upper bound on the approximation error of the estimators. We derive a doubly robust test statistic, which employs a nonparametric estimation but achieves a parametric convergence rate. We further adopt sample splitting and cross-fitting to minimize the conditions required to ensure the consistency of the test. We demonstrate the efficacy of the test through both simulations and the three data applications.

A Generic Approach for Reproducible Model Distillation

Model distillation has been a popular method for producing interpretable machine learning. It uses an interpretable "student" model to mimic the predictions made by the black box "teacher" model. However, when the student model is sensitive to the variability of the data sets used for training, the corresponded interpretation is not reliable. Existing strategies stabilize model distillation by checking whether a large enough corpus of pseudo-data is generated to reliably reproduce student models, but methods to do so have so far been developed for a specific student model. In this paper, we develop a generic approach for stable model distillation based on central limit theorem for the average loss. We start with a collection of candidate student models and search for candidates that reasonably agree with the teacher. Then we construct a multiple testing framework to select a corpus size such that the consistent student model would be selected under different pseudo sample. We demonstrate the application of our proposed approach on three commonly used intelligible models: decision trees, falling rule lists and symbolic regression. Finally, we conduct simulation experiments on Mammographic Mass and Breast Cancer datasets and illustrate the testing procedure throughout a theoretical analysis with Markov process.

Optimizing Pessimism in Dynamic Treatment Regimes: A Bayesian Learning Approach

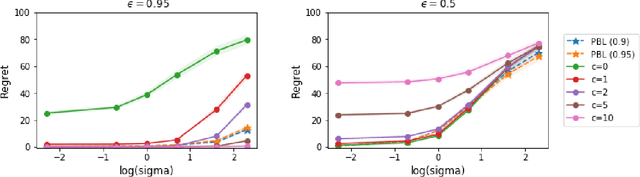
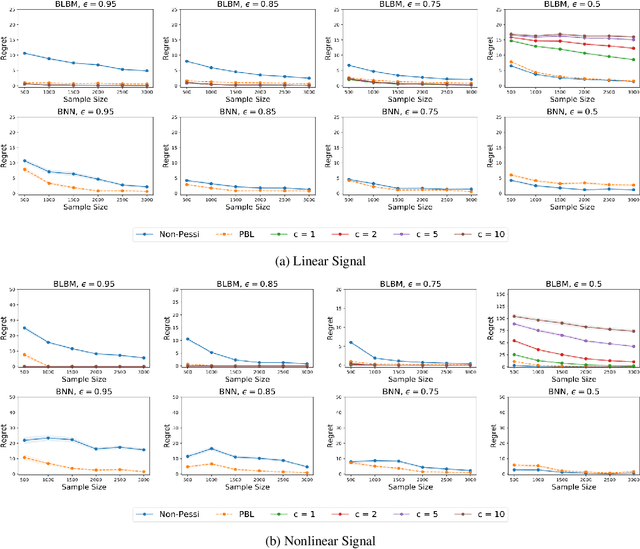
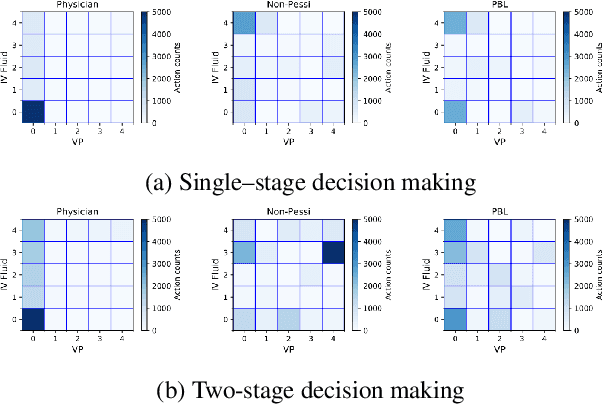
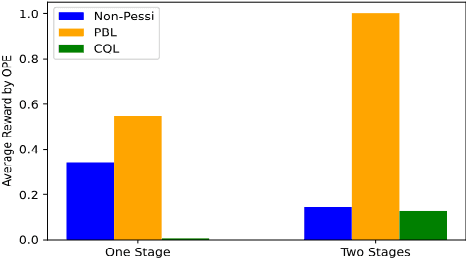
In this article, we propose a novel pessimism-based Bayesian learning method for optimal dynamic treatment regimes in the offline setting. When the coverage condition does not hold, which is common for offline data, the existing solutions would produce sub-optimal policies. The pessimism principle addresses this issue by discouraging recommendation of actions that are less explored conditioning on the state. However, nearly all pessimism-based methods rely on a key hyper-parameter that quantifies the degree of pessimism, and the performance of the methods can be highly sensitive to the choice of this parameter. We propose to integrate the pessimism principle with Thompson sampling and Bayesian machine learning for optimizing the degree of pessimism. We derive a credible set whose boundary uniformly lower bounds the optimal Q-function, and thus does not require additional tuning of the degree of pessimism. We develop a general Bayesian learning method that works with a range of models, from Bayesian linear basis model to Bayesian neural network model. We develop the computational algorithm based on variational inference, which is highly efficient and scalable. We establish the theoretical guarantees of the proposed method, and show empirically that it outperforms the existing state-of-the-art solutions through both simulations and a real data example.

Testing Directed Acyclic Graph via Structural, Supervised and Generative Adversarial Learning

In this article, we propose a new hypothesis testing method for directed acyclic graph (DAG). While there is a rich class of DAG estimation methods, there is a relative paucity of DAG inference solutions. Moreover, the existing methods often impose some specific model structures such as linear models or additive models, and assume independent data observations. Our proposed test instead allows the associations among the random variables to be nonlinear and the data to be time-dependent. We build the test based on some highly flexible neural networks learners. We establish the asymptotic guarantees of the test, while allowing either the number of subjects or the number of time points for each subject to diverge to infinity. We demonstrate the efficacy of the test through simulations and a brain connectivity network analysis.