Double Fairness Policy Learning: Integrating Action Fairness and Outcome Fairness in Decision-making

Fairness is a central pillar of trustworthy machine learning, especially in domains where accuracy- or profit-driven optimization is insufficient. While most fairness research focuses on supervised learning, fairness in policy learning remains less explored. Because policy learning is interventional, it induces two distinct fairness targets: action fairness (equitable action assignments) and outcome fairness (equitable downstream consequences). Crucially, equalizing actions does not generally equalize outcomes when groups face different constraints or respond differently to the same action. We propose a novel double fairness learning (DFL) framework that explicitly manages the trade-off among three objectives: action fairness, outcome fairness, and value maximization. We integrate fairness directly into a multi-objective optimization problem for policy learning and employ a lexicographic weighted Tchebyshev method that recovers Pareto solutions beyond convex settings, with theoretical guarantees on the regret bounds. Our framework is flexible and accommodates various commonly used fairness notions. Extensive simulations demonstrate improved performance relative to competing methods. In applications to a motor third-party liability insurance dataset and an entrepreneurship training dataset, DFL substantially improves both action and outcome fairness while incurring only a modest reduction in overall value.

Beyond Demand Estimation: Consumer Surplus Evaluation via Cumulative Propensity Weights

This paper develops a practical framework for using observational data to audit the consumer surplus effects of AI-driven decisions, specifically in targeted pricing and algorithmic lending. Traditional approaches first estimate demand functions and then integrate to compute consumer surplus, but these methods can be challenging to implement in practice due to model misspecification in parametric demand forms and the large data requirements and slow convergence of flexible nonparametric or machine learning approaches. Instead, we exploit the randomness inherent in modern algorithmic pricing, arising from the need to balance exploration and exploitation, and introduce an estimator that avoids explicit estimation and numerical integration of the demand function. Each observed purchase outcome at a randomized price is an unbiased estimate of demand and by carefully reweighting purchase outcomes using novel cumulative propensity weights (CPW), we are able to reconstruct the integral. Building on this idea, we introduce a doubly robust variant named the augmented cumulative propensity weighting (ACPW) estimator that only requires one of either the demand model or the historical pricing policy distribution to be correctly specified. Furthermore, this approach facilitates the use of flexible machine learning methods for estimating consumer surplus, since it achieves fast convergence rates by incorporating an estimate of demand, even when the machine learning estimate has slower convergence rates. Neither of these estimators is a standard application of off-policy evaluation techniques as the target estimand, consumer surplus, is unobserved. To address fairness, we extend this framework to an inequality-aware surplus measure, allowing regulators and firms to quantify the profit-equity trade-off. Finally, we validate our methods through comprehensive numerical studies.

InSPO: Unlocking Intrinsic Self-Reflection for LLM Preference Optimization

Direct Preference Optimization (DPO) and its variants have become standard for aligning Large Language Models due to their simplicity and offline stability. However, we identify two fundamental limitations. First, the optimal policy depends on arbitrary modeling choices (scalarization function, reference policy), yielding behavior reflecting parameterization artifacts rather than true preferences. Second, treating response generation in isolation fails to leverage comparative information in pairwise data, leaving the model's capacity for intrinsic self-reflection untapped. To address it, we propose Intrinsic Self-reflective Preference Optimization (InSPO), deriving a globally optimal policy conditioning on both context and alternative responses. We prove this formulation superior to DPO/RLHF while guaranteeing invariance to scalarization and reference choices. InSPO serves as a plug-and-play enhancement without architectural changes or inference overhead. Experiments demonstrate consistent improvements in win rates and length-controlled metrics, validating that unlocking self-reflection yields more robust, human-aligned LLMs.

PASTA: A Unified Framework for Offline Assortment Learning

We study a broad class of assortment optimization problems in an offline and data-driven setting. In such problems, a firm lacks prior knowledge of the underlying choice model, and aims to determine an optimal assortment based on historical customer choice data. The combinatorial nature of assortment optimization often results in insufficient data coverage, posing a significant challenge in designing provably effective solutions. To address this, we introduce a novel Pessimistic Assortment Optimization (PASTA) framework that leverages the principle of pessimism to achieve optimal expected revenue under general choice models. Notably, PASTA requires only that the offline data distribution contains an optimal assortment, rather than providing the full coverage of all feasible assortments. Theoretically, we establish the first finite-sample regret bounds for offline assortment optimization across several widely used choice models, including the multinomial logit and nested logit models. Additionally, we derive a minimax regret lower bound, proving that PASTA is minimax optimal in terms of sample and model complexity. Numerical experiments further demonstrate that our method outperforms existing baseline approaches.

Quantile-Optimal Policy Learning under Unmeasured Confounding

We study quantile-optimal policy learning where the goal is to find a policy whose reward distribution has the largest $\alpha$-quantile for some $\alpha \in (0, 1)$. We focus on the offline setting whose generating process involves unobserved confounders. Such a problem suffers from three main challenges: (i) nonlinearity of the quantile objective as a functional of the reward distribution, (ii) unobserved confounding issue, and (iii) insufficient coverage of the offline dataset. To address these challenges, we propose a suite of causal-assisted policy learning methods that provably enjoy strong theoretical guarantees under mild conditions. In particular, to address (i) and (ii), using causal inference tools such as instrumental variables and negative controls, we propose to estimate the quantile objectives by solving nonlinear functional integral equations. Then we adopt a minimax estimation approach with nonparametric models to solve these integral equations, and propose to construct conservative policy estimates that address (iii). The final policy is the one that maximizes these pessimistic estimates. In addition, we propose a novel regularized policy learning method that is more amenable to computation. Finally, we prove that the policies learned by these methods are $\tilde{\mathscr{O}}(n^{-1/2})$ quantile-optimal under a mild coverage assumption on the offline dataset. Here, $\tilde{\mathscr{O}}(\cdot)$ omits poly-logarithmic factors. To the best of our knowledge, we propose the first sample-efficient policy learning algorithms for estimating the quantile-optimal policy when there exist unmeasured confounding.

Reinforcement Learning with Continuous Actions Under Unmeasured Confounding

This paper addresses the challenge of offline policy learning in reinforcement learning with continuous action spaces when unmeasured confounders are present. While most existing research focuses on policy evaluation within partially observable Markov decision processes (POMDPs) and assumes discrete action spaces, we advance this field by establishing a novel identification result to enable the nonparametric estimation of policy value for a given target policy under an infinite-horizon framework. Leveraging this identification, we develop a minimax estimator and introduce a policy-gradient-based algorithm to identify the in-class optimal policy that maximizes the estimated policy value. Furthermore, we provide theoretical results regarding the consistency, finite-sample error bound, and regret bound of the resulting optimal policy. Extensive simulations and a real-world application using the German Family Panel data demonstrate the effectiveness of our proposed methodology.

Offline Dynamic Inventory and Pricing Strategy: Addressing Censored and Dependent Demand

In this paper, we study the offline sequential feature-based pricing and inventory control problem where the current demand depends on the past demand levels and any demand exceeding the available inventory is lost. Our goal is to leverage the offline dataset, consisting of past prices, ordering quantities, inventory levels, covariates, and censored sales levels, to estimate the optimal pricing and inventory control policy that maximizes long-term profit. While the underlying dynamic without censoring can be modeled by Markov decision process (MDP), the primary obstacle arises from the observed process where demand censoring is present, resulting in missing profit information, the failure of the Markov property, and a non-stationary optimal policy. To overcome these challenges, we first approximate the optimal policy by solving a high-order MDP characterized by the number of consecutive censoring instances, which ultimately boils down to solving a specialized Bellman equation tailored for this problem. Inspired by offline reinforcement learning and survival analysis, we propose two novel data-driven algorithms to solving these Bellman equations and, thus, estimate the optimal policy. Furthermore, we establish finite sample regret bounds to validate the effectiveness of these algorithms. Finally, we conduct numerical experiments to demonstrate the efficacy of our algorithms in estimating the optimal policy. To the best of our knowledge, this is the first data-driven approach to learning optimal pricing and inventory control policies in a sequential decision-making environment characterized by censored and dependent demand. The implementations of the proposed algorithms are available at https://github.com/gundemkorel/Inventory_Pricing_Control

Two-way Deconfounder for Off-policy Evaluation in Causal Reinforcement Learning

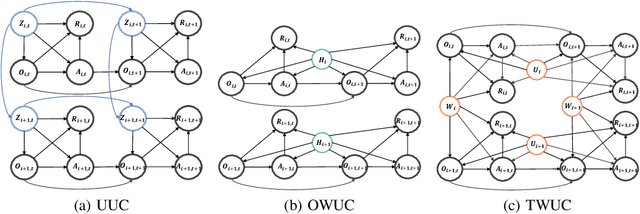
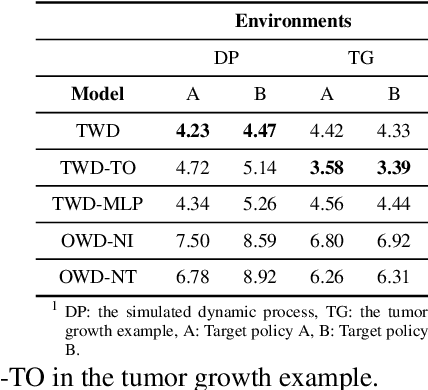
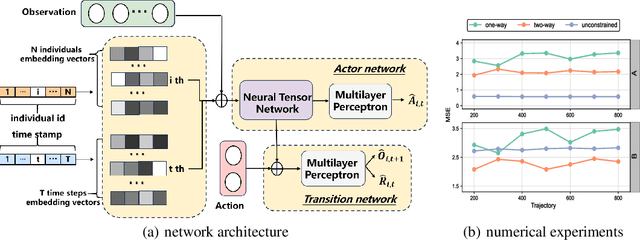
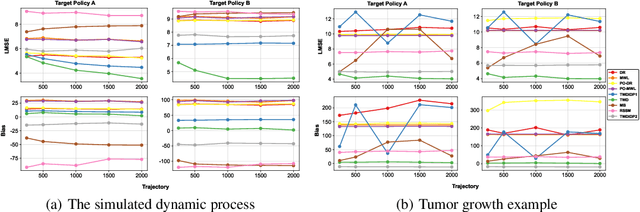
This paper studies off-policy evaluation (OPE) in the presence of unmeasured confounders. Inspired by the two-way fixed effects regression model widely used in the panel data literature, we propose a two-way unmeasured confounding assumption to model the system dynamics in causal reinforcement learning and develop a two-way deconfounder algorithm that devises a neural tensor network to simultaneously learn both the unmeasured confounders and the system dynamics, based on which a model-based estimator can be constructed for consistent policy value estimation. We illustrate the effectiveness of the proposed estimator through theoretical results and numerical experiments.

A Tale of Two Cities: Pessimism and Opportunism in Offline Dynamic Pricing

This paper studies offline dynamic pricing without data coverage assumption, thereby allowing for any price including the optimal one not being observed in the offline data. Previous approaches that rely on the various coverage assumptions such as that the optimal prices are observable, would lead to suboptimal decisions and consequently, reduced profits. We address this challenge by framing the problem to a partial identification framework. Specifically, we establish a partial identification bound for the demand parameter whose associated price is unobserved by leveraging the inherent monotonicity property in the pricing problem. We further incorporate pessimistic and opportunistic strategies within the proposed partial identification framework to derive the estimated policy. Theoretically, we establish rate-optimal finite-sample regret guarantees for both strategies. Empirically, we demonstrate the superior performance of the newly proposed methods via a synthetic environment. This research provides practitioners with valuable insights into offline pricing strategies in the challenging no-coverage setting, ultimately fostering sustainable growth and profitability of the company.

Learning Robust Treatment Rules for Censored Data

There is a fast-growing literature on estimating optimal treatment rules directly by maximizing the expected outcome. In biomedical studies and operations applications, censored survival outcome is frequently observed, in which case the restricted mean survival time and survival probability are of great interest. In this paper, we propose two robust criteria for learning optimal treatment rules with censored survival outcomes; the former one targets at an optimal treatment rule maximizing the restricted mean survival time, where the restriction is specified by a given quantile such as median; the latter one targets at an optimal treatment rule maximizing buffered survival probabilities, where the predetermined threshold is adjusted to account the restricted mean survival time. We provide theoretical justifications for the proposed optimal treatment rules and develop a sampling-based difference-of-convex algorithm for learning them. In simulation studies, our estimators show improved performance compared to existing methods. We also demonstrate the proposed method using AIDS clinical trial data.